二叉树后序遍历（递归+非递归）Java

---

一、结构

二、遍历二叉树

这块内容是二叉树最核心的部分。不但要掌握七种遍历的写法，前、中、后序的递归、非递归写法+层次遍历，还有学会（1）用前、中、后序遍历数组创建二叉树；（2）用一维数组存储二叉树。

1.后序遍历（递归）

前序遍历访问节点的顺序是 左儿子-右儿子-根节点。

代码

public void postOrderRecur(Node root) {
		if (root == null) {
			return;
		}
		postOrderRecur(root.left);
		postOrderRecur(root.right);
		System.out.print(root.data + " -> ");
	}

注意：这个代码是不是很眼熟呢？其实就是把前序或中序遍历中的一行代码换了个位置。

图解

初始。

第一步：
（1）执行postOrderRecur（Node root）方法，root不为null，于是调用postOrderRecur（root.left）方法，访问节点B；
（2）B不为空，继续调用postOrderRecur（B.left）方法，访问节点D；
（3）D不为空，调用postOrderRecur（D.left）方法，D.left为空，返回；
（4）调用postOrderRecur（D.right）方法，访问节点H；
（5）H不为空，调用postOrderRecur（H.left）方法，H.left为空，返回；
（6）调用postOrderRecur（H.right）方法，H.right为空，返回；
（7）打印“H”。

第二步：
（1）打印“H”的语句执行完后，其所在的方法结束，返回上一级方法；
（2）打印“D”。

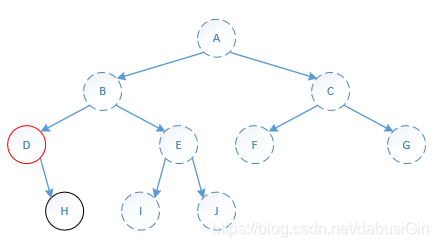
第三步：
（1）打印“D”的语句执行完后，其所在的方法结束，返回到上一级方法；
（2）调用postOrderRecur（B.right）方法，访问节点E；
（3）递归调用postOrderRecur（E.left）方法，访问节点I；
（4）递归调用postOrderRecur（I.left）方法，I.left为空，返回；
（5）递归调用postOrderRecur（I.right）方法，H.right为空，返回；
（6）打印“I”。

第四步：
（1）打印“I”的语句执行完后，其所在的方法结束，返回到上一级方法；
（2）调用postOrderRecur（E.right）方法，访问节点J；
（3）递归调用postOrderRecur（J.left）方法，J.left为空，返回；
（4）递归调用postOrderRecur（J.right）方法，J.right为空，返回；
（5）打印“J”。

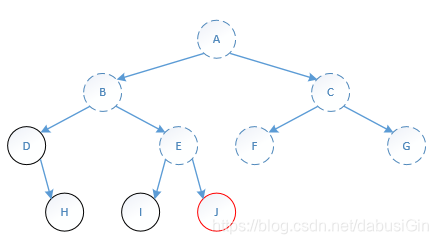
第五步：
（1）打印“J”的语句执行完后，其所在的方法结束，返回到上一级方法；
（2）打印“E”。

第六步：
（1）打印“E”的语句执行完后，其所在的方法结束，返回到上一级方法；
（2）打印“B”。

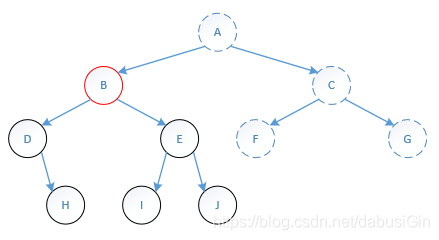
第七步：
（1）打印“E”的语句执行完后，其所在的方法结束，返回到上一级方法；
（2）调用postOrderRecur（A.right）方法，访问节点C；
（3）递归调用postOrderRecur（C.left）方法，访问节点F；
（4）递归调用postOrderRecur（F.left）方法，F.left为空，返回；
（5）递归调用postOrderRecur（F.right）方法，F.right为空，返回；
（6）打印“F”。

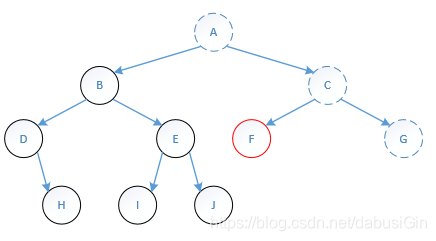
第八步：
（1）打印“F”的语句执行完后，其所在的方法结束，返回到上一级方法；
（2）调用postOrderRecur（C.right）方法，访问节点G；
（3）递归调用postOrderRecur（G.left）方法，G.left为空，返回；
（4）递归调用postOrderRecur（G.right）方法，G.right为空，返回；
（5）打印“G”。

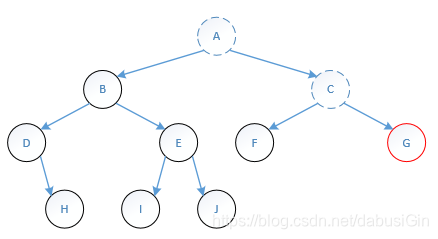
第九步：

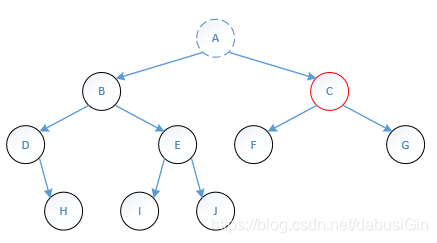
第十步：

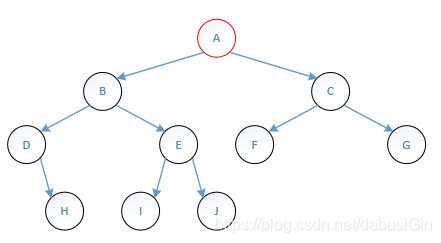
打印顺序：HDIJEBFGCA

2.后序遍历（非递归）

代码

要实现访问顺序为左儿子-右儿子-根节点，可以利用后进先出的栈，在节点不为空的情况下，依次将根节点、右儿子、左儿子压入一个栈中，最后一起打印栈中的元素。

public void postOrder() {
		Node current = root;
		//就是图中的S1，把LinkedList作为栈使用
		LinkedList<Node> s1 = new LinkedList<Node>();
		//就是图中的S2，把LinkedList作为栈使用
		LinkedList<Node> s2 = new LinkedList<Node>();
		while (current != null || !s1.isEmpty()) {
			while (current != null) {
				s1.addFirst(current);
				s2.addFirst(current);
				current = current.right;
			}
			if (!s1.isEmpty()) {
				current = s1.removeFirst();
				current = current.left;
			}
		}
		while (!s2.isEmpty()) {
			System.out.print(s2.removeFirst().data + " -> ");
		}
	}

图解

初始。

图一：

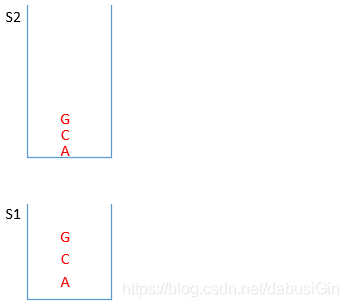
图二：

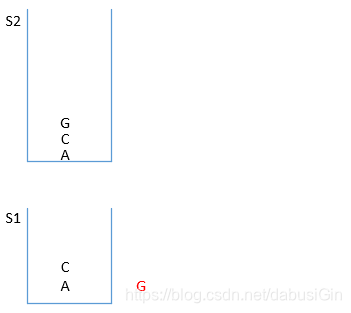
图三：

图四：

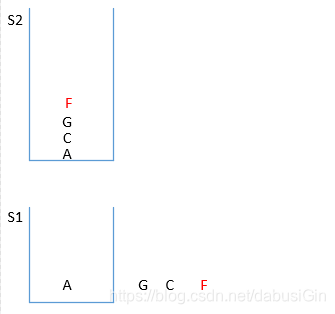
图五：

图六：

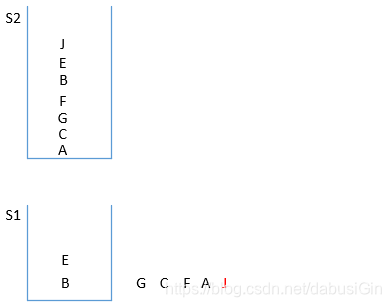
图七：

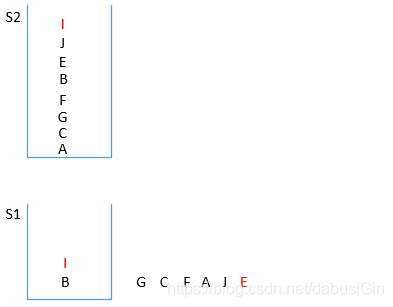
图八：

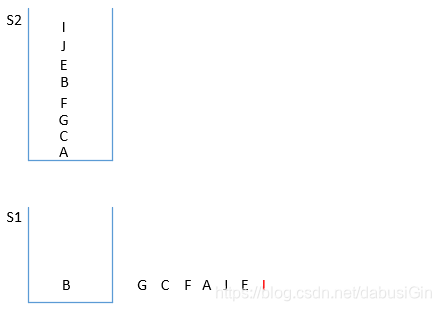
图九：

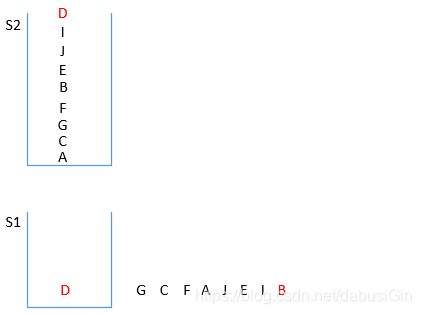
图十：

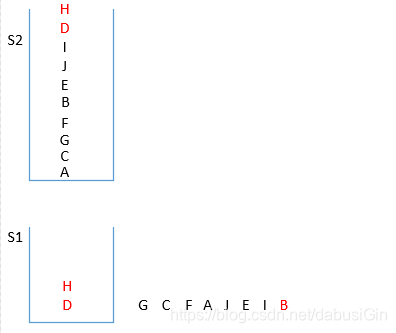
图十一：

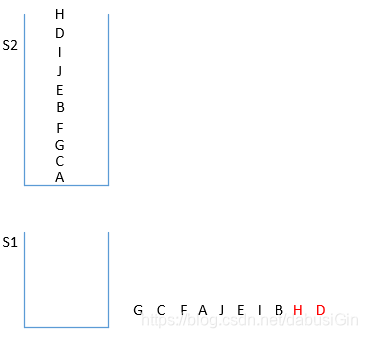
最后再从栈S2取出元素，得到打印顺序为HDIJEBFGCA