跳跃表（SkipList）从原理到实现

最新推荐文章于 2024-02-21 12:12:22 发布

原创

最新推荐文章于 2024-02-21 12:12:22 发布 · 721 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#跳跃表 #数据结构

跳跃表是一种基于链表的数据结构，通过多层有序链表实现高效的查找、插入和删除操作，时间复杂度达到O(lg(n))。它利用随机概率使得元素分布近似均匀，从而在保持链表操作简便的同时提升性能。文章详细介绍了跳跃表的原理和实现方法。

你也可以通过我的独立博客 —— www.huliujia.com 获取本篇文章

数组与链表

数组和链表是非常基础的两种数据结构，链表每次查找都需要从头结点开始线性遍历，时间复杂度是O(n)。而数组通过维护元素顺序可以使用二分查找，查找的时间复杂度是O(lg(n))。查找效率方面数组完胜链表。

但是由于数组插入或删除元素时必须要移动所有受影响的节点，所以时间复杂度是O(n).并且数组的长度是固定的，当空间不够时需要重新分配内存。而链表插入和删除元素只需要改动少量指针即可，时间复杂度是O(1)。但是因为插入和删除一半都需要先查找元素，所以实际上链表的插入和删除时间复杂度还是O(n)。

今天介绍一种基于链表的数据结构 —— 跳跃表(Skiplist)，在保持链表便于插入、删除的特性同时，可以把查找、插入、删除的时间复杂度降到O(lg(n))。

跳跃表的原理

数组能够实现查找时间复杂度O(lg(n))，主要是因为二分查找每次都可以排除一半的元素，那么链表有没有办法也每次排除一半的元素呢？

显然，原生的链表每次只能排除一个元素(当前元素），想要排除一半的元素需要满足两个条件，首先是链表必须是有序的，其次是能够访问到最中间的元素，这个其实就是数组二分查找的原理。

让链表有序是一个比较容易实现的需求，那么如何访问到最中间的元素呢？我们可以使用一个外部节点来保存中间节点。
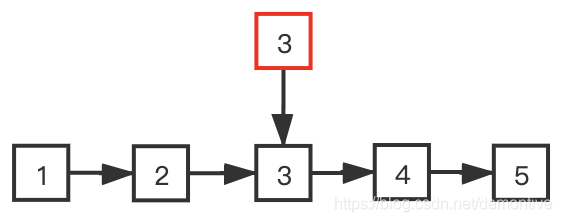
在这里插入图片描述
比如上图是一个有5个元素的有序链表，红色的元素3指向了中间的元素3，如果我们想要查找4，通过和中间元素3进行比较，很容易判断要查找的元素在3的右侧，那么就排除了3左侧的所有节点了。

上面的链表只有5个元素，那如果链表有更多的元素，比如8个元素呢？显然一个外部节点只能完成一次元素排除，如果想每次访问都能排除一半的元素，即需要更多的外部节点了。
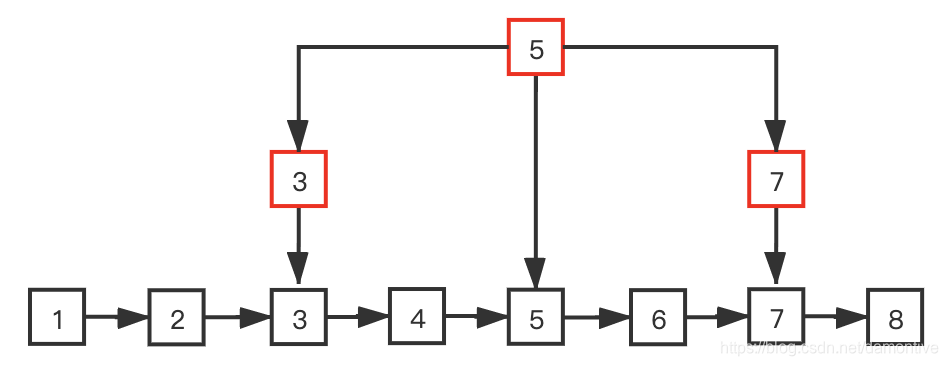
在这里插入图片描述
比如上图链表中有8个元素，总共使用了3个外部节点，外部节点分成了两层，通过和最上层外部节点元素5比较，我们可以排除掉一半的元素，剩下的元素和元素3或者元素7比较，可以再排除掉一半的元素。