Andrew Ng机器学习课程笔记（十九）之强化学习

Preface

Markov Decision Processes（MDP，马尔科夫决策过程）
Value Function（价值函数）
Value Iteration（值迭代）
Policy Iteration（迭代策略）
Parameter Estimation（参数估计）

Markov Decision Processes

MDP定义

马尔科夫决策过程MDP由一个五元组$(S,A,\{P_{sa}\},\gamma,R)$构成。
$S$表示状态集（states）。（对于自动直升机系统例子，直升机位置坐标和方向的集合）
$A$表示一组动作（actions）。（对于自动直升机系统例子，使用控制杆操纵的直升机飞行方向，让其向前，向后等）
$P_{sa}$是状态转换分布。$\sum_{s^{'}}P_{sa}(s^{'})=1,P_{sa}(s^{'}) \geq0$。$S$中的一个状态到另一个状态的转变，需要$A$来参与。$P_{sa}$表示的 是在当前$s ∈ S$状态下，经过$a ∈ A$作用后，会转移到的其他状态的概率分布情况（当前状态执行 a 后可能跳转到很多状态）。
$\gamma∈ [0,1)$是阻尼系数（discount factor）。
$R:S×A ⟼ ℝ$，$R$是回报函数（reward function），回报函数经常写作$R$的函数（只与$R$有关），这样的话，$R$重新写作$R:S ⟼ ℝ$。

MDP例子

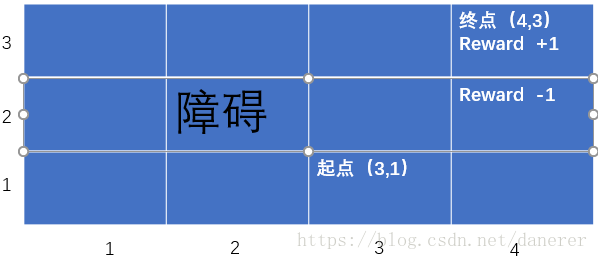
如图，假设有一个机器人生活在上述的网格世界中，从起点（3，1）出发要到达终点（3，2）。
（我们使用reward +1来关联我们希望它到达的网格单元位置；reward -1来关联我们希望它避免的网格单元位置）

对照MDP定义我们可以得到：
$S=\{(1,1),(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4)\}$。
$A=\{N,S,E,W\}$。（北，南，东，西）
由于机器人在移动中存在一定的噪声（误差），所以有当机器人想要向N移动时，有0.1的可能行向W移动，0.1的可能行向E移动，0.8的可能行向N移动。即，例如当机器人在起点想要向N移动时，$P_{(3,1),N}((3,2))=0.8,P_{(3,1),N}((4,1))=0.1,P_{(3,1),N}((2,1))=0.1,P_{(3,1),N}((3，3))=0$。同时，当机器人撞墙时，机器人保持不动。
回报函数：$R((4,3))=+1$，$R((4,2))=-1$，$R(other \;\;S)=-0.02$($R(other \;\;S)$可以理解为每一步的消耗，使机器人尽快到达目的地)。

MDP过程

假设$s_i$表示在时刻 i 的状态，$a_i$表示在时刻 i 的状态将要进行的动作。所以在时刻 0 时的状态为$s_0$，然后选择一个 $a_0$，根据$s_1 \sim P_{s_{0}a_{0}}$这个分布函数得到在时刻 1 时的状态$s_1$。然后在时刻 1 时的状态为$s_1$，然后选择一个 $a_1$，根据$s_2 \sim P_{s_{1}a_{1}}$这个分布函数得到在时刻 2 时的状态$s_2$。依次类推，在时刻 i 时的状态为$s_i$，然后选择一个 $a_i$，根据$s_{i+1} \sim P_{s_{i}a_{i}}$这个分布函数得到在时刻 i+1 时的状态$s_{i+1}$。

通过上述过程我们得到一系列的时序状态$S_t=\{s_1,s_2,...,s_{i-1},s_i,s_{i+1},...\}$。

为了评估我们的机器人学习的效率（做得好不好），我们计算这个时序状态的回报函数之和：

$$\begin{aligned} R(s_0)+R(s_1)+R(s_2)+\;\;... \end{aligned}$$

我们使用阻尼系数（discount factor）$\gamma∈ [0,1)$来表示当前状态对于时序状态的回报函数之和的影响要大于以后状态对于时序状态的回报函数之和的影响：

$$\begin{aligned} R(s_0)+\gamma\;R(s_1)+\gamma^2\;R(s_2)+\;\;... \end{aligned}$$

所以这个强化学习算法的周期总是基于已有的状态信息来进行动作和下一步状态的转换，我们期望得到的是时序状态的回报函数之和的最大值，即：

$$\begin{aligned} E[R(s_0)+\gamma\;R(s_1)+\gamma^2\;R(s_2)+\;\;...] \end{aligned}$$

为了得到的是时序状态的回报函数之和$E[R(s_0)+\gamma\;R(s_1)+\gamma^2\;R(s_2)+\;\;...]$的最大值，我们需要知道在当前状态下应该采取什么行动。我们将这个动作的选择过程称为策略（policy），每一个 policy 其实就是一个状态到动作的映射函数$π ∶ S ⟼ A$，我们使用$\pi$来表示这个策略的集合。

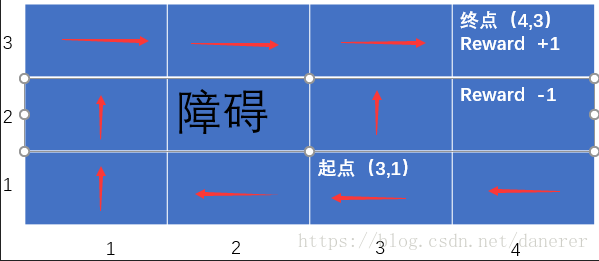
很明显上图所示的策略集合$\pi$并不是一个最佳的策略集合，你可能会想在起点（3，1）时为什么不直接从（3，2），（3，3），（3，4）的最短路径到达终点，而是要走一圈绕路，这是由于在（3，2）有 0.1 的概率进入（4，2）这会造成大的失误，所以MDP过程采用了一种微妙的折中的方法。

Value Function

对于任一策略集合$\pi$，定义值函数（Value Function）$V^{\pi}:S ⟼\mathbb R$的映射，$V^{\pi}(S)$时序状态的回报函数的总和的预期值，即为：

$$\begin{aligned} V^{\pi}(s)=E[R(s_0)+\gamma\;R(s_1)+\gamma^2\;R(s_2)+\;\;..|\pi,s_0=s] \end{aligned}$$

对于下述的的一个策略集合$\pi$与它的时序状态的回报函数的总和的预期值$V^{\pi}(s)$：


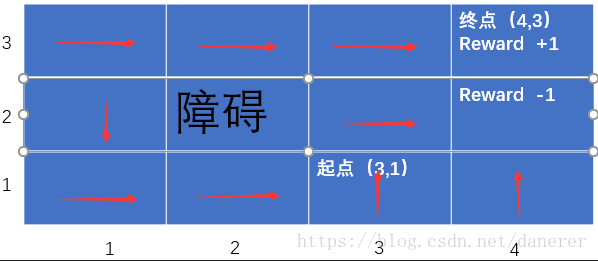
我们可以明显看出这不是一个好的策略集合$\pi$。

对于价值函数我们可以进行下述过程：

$$\begin{aligned} V^{\pi}(s)&=E[R(s_0)+\gamma\;R(s_1)+\gamma^2\;R(s_2)+\;\;..|\pi,s_0=s] \\ &=E[R(s_0)+\gamma\;(R(s_1)+\gamma\;R(s_2)+\;\;..)|\pi,s_0=s] \end{aligned}$$

所以有：

$$\begin{aligned} V^{\pi}(s)&=R(s_0)+E[\gamma\;(R(s_1)+\gamma\;R(s_2)+\;\;..)|\pi,s_0=s]\\ &=R(s_0)+\gamma\;E[R(s_1)+\gamma\;R(s_2)+\;\;..|\pi,s_0=s] \end{aligned}$$

其中，$V^{\pi}(s_1)=E[R(s_1)+\gamma\;R(s_2)+\;\;..|\pi,s_0=s]$。所以：

$$\begin{aligned} V^{\pi}(s)=R(s_0)+V^{\pi}(s_1) \end{aligned}$$

上式分成了两个部分，第一部分称为当前时刻的即时回报，第二部分称为当前时刻的未来回报。
同时，由于对于当前状态$s$采用行动$\pi(s)$得到的下一个状态$s^{'}$是随机的，所以有Bellman等式：

$$\begin{aligned} V^{\pi}(s)=R(s)+\gamma \sum_{s^{'} \in S} P_{s\pi(s)}(s^{'}) V^{\pi}(s^{'}) \end{aligned}$$

举一个具体的例子说明上式。假设$\pi((3,1))=N$且当期状态为$s=(3,1)$，所以$V^{\pi}(s)$为：

$$\begin{aligned} V^{\pi}(s)=V^{\pi}((3,1))=R((3,1))+\gamma [0.8*V^{\pi}((3,2))+0.1*V^{\pi}((4,1))+0.1*V^{\pi}((2,1))] \end{aligned}$$

如果我们将状态集合$S$中的所以状态都用Bellman等式表示，我们可以得到由11个方程与11个未知数组成的方程组，进而求得每一个状态的$V^{\pi}(s)$。

所以最优值函数的定义为：

$$\begin{aligned} V^{*}(s)=\text{max}_{\pi}\;\;V^{\pi}(s^{}) \end{aligned}$$

所以有最优值函数$V^{*}(s)$的Bellman等式为:

$$\begin{aligned} V^{\pi}(s)=R(s)+\text{max}_{a\in A}\;\;\gamma \sum_{s^{'} \in S} P_{sa}(s^{'}) V^{*}(s^{'}) \end{aligned}$$

所以最优策略为：

$$\begin{aligned} \pi^{*}(s)=\text{arg}\;\text{max}_{a\in A}\;\sum_{s^{'} \in S} P_{sa}(s^{'}) V^{*}(s^{'}) \end{aligned}$$

所以最优策略集合$p^*$为$\pi^{*}(s)$的集合。

Value Iteration

Value Iteration（值迭代）的过程为：

1. 将$S$中每一个 s 的$V(s)$初始化为 0 。

2. Repeat until convergence{
   更新每一个 s 的$V(s)$，
   

   $$\begin{aligned}V^{}(s):=R(s)+\text{max}_{a\in A}\;\;\gamma \sum_{s^{'} \in S} P_{sa}(s^{'}) V^{}(s^{'})\end{aligned}$$

   }

上述值迭代过程的第二步循环的实现有两种策略：

1. 同步更新：拿初始化后的第一次迭代来说吧，初始状态所有的$V(s)$为 0 。然后对所有的 s 都计算新的$V(s)=R(s)+0=R(s)$。在计算每一个状态时，得到新的$V(s)$后，先存下来不立即更新。待所有的 s 的新值$V(s)$都计算完毕后，再统一更新。 这样，第一次迭代后，V(s)=R(s)。即为，每一次的迭代与上一次的迭代有关，不与当前迭代轮次中最新产生的$V(s)$相关。
2. 异步更新：对每一个状态 s，得到新的$V(s)$后，立即更新。这样，第一次迭代后，大部分$V(s)>R(s)$。即为，每一次的迭代既与于上一次的迭代有关，也与当前迭代轮次中最新产生的$V(s)$相关。

通过值迭代，我们得到：

继而我们可以得到策略集合$\pi$：

在这里我们就可以解释很明显上图所示的策略集合$\pi$在起点(3,1)时为什么不直接从(3,2)，(3,3)，(3,4)的最短路径到达终点，而是要走一圈绕路。
如果我们在(3,1)选择$W \in A$，预期总收益为：

$$\begin{aligned} &\text{W:}\;\sum_{s^{'} \in S} P_{sa}(s^{'}) V^{*}(s^{'})\\ &=0.8*0.75+0.1*0.69+0.1*0.71\\ &=0.740 \end{aligned}$$

如果我们在(3,1)选择$N \in A$，预期总收益为：

$$\begin{aligned} &\text{N:}\;\sum_{s^{'} \in S} P_{sa}(s^{'}) V^{*}(s^{'})\\ &=0.1*0.75+0.8*0.69+0.1*0.49\\ &=0.676 \end{aligned}$$

这就是为什么不直接从(3,2)，(3,3)，(3,4)的最短路径到达终点，而是要走一圈绕路的原因。

Policy Iteration

Policy Iteration（策略迭代）的过程为：

1. 将$\pi$中每一个$\pi(s)$的随机初始化为$A=\{W,N,E,S\}$中的任意值。

2. Repeat until convergence{
   1.$V:=V^{\pi}$。（$V^{\pi}(s)=R(s)+\gamma \sum_{s^{‘} \in S} P_{s\pi(s)}(s^{‘}) V^{\pi}(s^{‘})$等式构成的方程组解得每一个$V^{\pi}(s)$）
   2.更新每一个 s 的$\pi(s)$，
   

   $$\begin{aligned} \pi^{}(s)=\text{arg}\;\text{max}_{a\in A}\;\sum_{s^{'} \in S} P_{sa}(s^{'}) V^{}(s^{'}) \end{aligned}$$

   }

Parameter Estimation

马尔科夫决策过程MDP是一个五元组$(S,A,\{P_{sa}\},\gamma,R)$问题。上面我们得到了处了$P_{sa}$之外的答案。$P_{sa}$的计算公式如下：

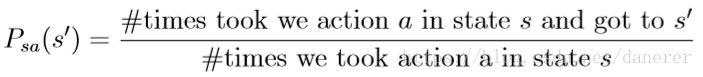
同时当出现0/0的情况时，设定$P_{sa}=1/|s|$。

当转移概率和回报函数（我们一般自己设定）估计出之后，我们可以使用值迭代或者策略迭代来解决 MDP 问题。比如，我们将参数估计和值迭代结合起来（在不知道状态转移概率情况下）的流程如下：

1. 将$\pi$中每一个$\pi(s)$的随机初始化为$A=\{W,N,E,S\}$中的任意值。

2. Repeat until convergence{
   1.在样本上统计π中每个状态转移次数，用来更新$P_{sa}$和 R
   2.$V:=V^{\pi}$。（$V^{\pi}(s)=R(s)+\gamma \sum_{s^{‘} \in S} P_{s\pi(s)}(s^{‘}) V^{\pi}(s^{‘})$等式构成的方程组解得每一个$V^{\pi}(s)$）
   3.更新每一个 s 的$\pi(s)$，
   

   $$\begin{aligned} \pi^{}(s)=\text{arg}\;\text{max}_{a\in A}\;\sum_{s^{'} \in S} P_{sa}(s^{'}) V^{}(s^{'}) \end{aligned}$$

   }