如果矩阵满足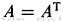
1.对称矩阵的对角化
如果一个矩阵有n个线性无关的特征向量,则矩阵是
可对角化的,矩阵可表示成
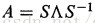 ,相应的
,相应的
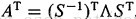 。因为
。因为
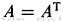 ,很有
可能A的逆等于A的转置。同样的,就
可能有
,很有
可能A的逆等于A的转置。同样的,就
可能有
 ,这可发现S中的特征向量和其他的特征向量正交,后文会进行证明。
,这可发现S中的特征向量和其他的特征向量正交,后文会进行证明。
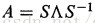 ,相应的
,相应的
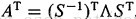 。因为
。因为
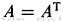 ,很有
可能A的逆等于A的转置。同样的,就
可能有
,很有
可能A的逆等于A的转置。同样的,就
可能有
 ,这可发现S中的特征向量和其他的特征向量正交,后文会进行证明。
,这可发现S中的特征向量和其他的特征向量正交,后文会进行证明。
我们把上的S成为正交矩阵Q,Q满足
 ,Q中的每一个列向量为单位特征向量。每一个对阵矩阵都可以被分解成
,Q中的每一个列向量为单位特征向量。每一个对阵矩阵都可以被分解成
 :
:
 ,Q中的每一个列向量为单位特征向量。每一个对阵矩阵都可以被分解成
,Q中的每一个列向量为单位特征向量。每一个对阵矩阵都可以被分解成
 :
:
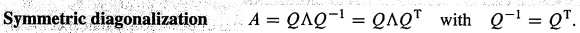
2.对称矩阵的性质
1.对阵矩阵的特征值为实数。

2.对阵矩阵的特征向量相互正交。
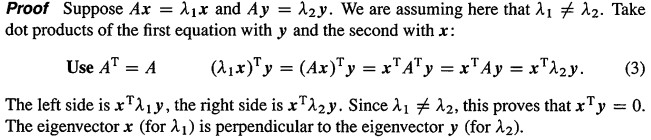
3.谱分解
先看一个例子:
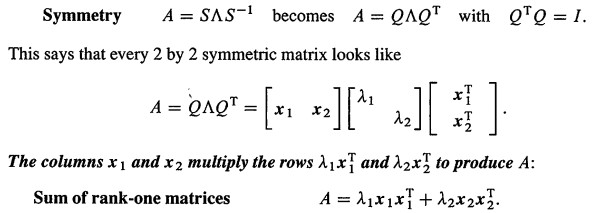
上面例子是矩阵的另一种分解形式,把矩阵A分解成了两个投影矩阵的线性组合。
下面介绍下什么是投影矩阵,如果一个
方阵满足
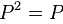 ,我们矩阵P为投影矩阵。
,我们矩阵P为投影矩阵。
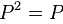 ,我们矩阵P为投影矩阵。
,我们矩阵P为投影矩阵。
现在我们有两个投影矩阵P1和P2,显然满足
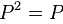 。
。
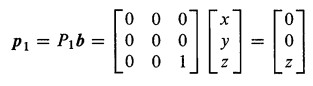
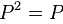 。
。

任意给定一个3维列向量b=(x,y,z),通过P1矩阵后得到列向量p1=(0,0,z),可以发现矩阵P把所有的向量都投影到了Z轴上面。
同样的P2把所有的向量都投影到xy平面上。
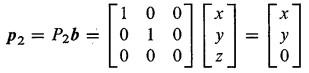
这里补充一个知识,如果想把向量投影到一条直线上,如何得到投影矩阵。给出一个最简单的方法,如果u是这条直线的单位方向向量,则投影矩阵P=uuT。详细的投影介绍见
wikip。
现在重新回到谱分解,现在考虑n*n的对阵矩阵,肯定存在n和投影矩阵
 ,可以把矩阵A看成n个投影矩阵的线性组合,这个就是谱分解。
,可以把矩阵A看成n个投影矩阵的线性组合,这个就是谱分解。
 ,可以把矩阵A看成n个投影矩阵的线性组合,这个就是谱分解。
,可以把矩阵A看成n个投影矩阵的线性组合,这个就是谱分解。
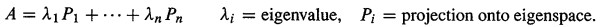
4.主元和特征值的关系
主元和特征值不同,但是他们又一定的联系:
1.对于所有矩阵,主元的乘积=特征值的乘积=矩阵的行列式
2.对于对称矩阵,主元和特征值有相同的符号,即正主元的个数和正特征值的个数相同,但是非对称矩阵不满足,下面是两个例子。
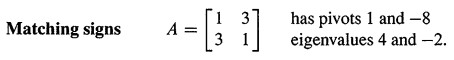
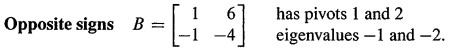
5.对角性
如果一个矩阵A的特征值都不相同,它的特征向量肯定线性无关,则A是可以对角化的。如果一个矩阵存在相同的特征值,对于非对称矩阵会导致特征向量不足,无法对角化;但对于对称矩阵,即使存在相同的特征值,矩阵仍然可以对角化。(在这就不做证明了)
6.Reference
《A Introduction to Linear Algebra》 GILBERT STRANG





















 5万+
5万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








