“二叉排序树,又称为二叉查找树。它或者是一颗空树,或者具有下列性质的二叉树。
-
若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
-
若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
-
它的左、右子树也分别为二叉排序树。
构造一颗二叉排序树的目的,其实并不是为了排序,而是为了提高查找和插入删除关键字的速度。不管怎么说,在一个有序数据集上的查找,速度总是要快于无序数据集的,而二叉排序树这种非线性的结构,也有利于插入和删除的实现。”
通俗的讲,二叉排序树的本质就是一颗二叉树,只是关键字的排序比较有规律,能够利用二叉树的递归特性进行很方便的操作。在对于二叉排序树的基本操作中,包括:根据数据集构建二叉排序树(没有要查找的关键字,就插入)、查找、删除。其中,删除操作时最麻烦的,插入和查找的思路很像,下面详解。
1、二叉排序树的查找操作
首先定义一个二叉树的结构。
- /* 二叉排序树的节点结构定义 */
- typedef struct BiTNode
- {
- int data;
- struct BiTNode *lchild, *rchild;
- } BiTNode, *BiTree;
查找操作思路:
先查找其根节点,如果根节点的数据与key值相等,则返回该根节点,并且返回TRUE;
否则, 如果key值大于根节点,则查询其右子树;
如果小于根节点,则查询其左子树。
代码如下:
- int SearchBST( BiTree T, int key, BiTree f, BiTree *p )
- {
- /* 递归查找二叉排序树T中是否存在key */
- /* 指针f指向T的双亲,其初始调用值为NULL */
- /* 若查找成功,则指针p指向该数据元素节点,并返回TRUE */
- /* 否则指针p指向查找路径上访问的最后一个节点并返回FALSE */
- if( !T )
- {
- *p = f; //这是f唯一被用到的位置。
- return FALSE;
- }
- else
- {
- if( key == T->data )
- { *p = T; return TRUE; }
- else if( key > T->data )
- return SearchBST( T->rchild, key, T, p ); /* 在右子树继续查找 */
- else
- return SearchBST( T->lchild, key, T, p ); /* 在左子树继续查找 */
- }
- }
- int SearchBST2( BiTree T, int key, BiTree f, BiTree *p )
- {
- /*非递归*/
- BiTree s;
- if( !T )
- { *p = f; return FALSE; }
- else
- {
- while( T )
- {
- if( key == T->data )
- { *p = T; return TRUE; }
- if( key > T->data )
- { s = T; T = T->rchild; }
- else
- { s = T; T = T->lchild; }
- }
- *p = s;
- return FALSE;
- }
- }
2、二叉排序树的插入操作
代码如下:
- int InsertBST1( BiTree *T, int key )
- {
- /* 当二叉排序树T中不存在关键字等于key的数据元素时 */
- /* 插入key并返回TRUE,否则返回FALSE */
- /* 调用查找函数SearchBST,非递归 */
- BiTree p, s;
- if( !SearchBST2( *T, key, NULL, &p ) )
- {
- s = (BiTree)malloc(sizeof(BiTNode));
- s->data = key;
- s->lchild = s->rchild = NULL;
- if( !p )
- *T = s; /* 插入s为根节点,此前树为空树 */
- else if( key > p->data )
- p->rchild = s; /* 插入s为右孩子 */
- else
- p->lchild = s; /* 插入s为左孩子 */
- return TRUE;
- }
- return FALSE;
- }
- int InsertBST2( BiTree *T, int key )
- {
- /* 当二叉排序树T中不存在关键字等于key的数据元素时 */
- /* 插入key并返回TRUE,否则返回FALSE */
- /* 未调用查找函数,递归插入 */
- if( !(*T) ) /* 树为空, */
- {
- (*T) = (BiTree)malloc(sizeof(BiTNode)); /* 这个位置要留心,要重新分配空间,*T为空,说明未曾分配空间 */
- (*T)->data = key;
- (*T)->lchild = (*T)->rchild = NULL;
- return TRUE;
- }
- if( key == (*T)->data )
- return FALSE;
- if( key > (*T)->data )
- return InsertBST2( &((*T)->rchild), key ); /* 插入右孩子 */
- else
- return InsertBST2( &((*T)->lchild), key ); /* 插入左孩子 */
- }
3、二叉树的删除操作(相对复杂一些)
删除节点有三种情况分析:
a. 叶子节点;(直接删除即可)
b. 仅有左或右子树的节点;(上移子树即可)
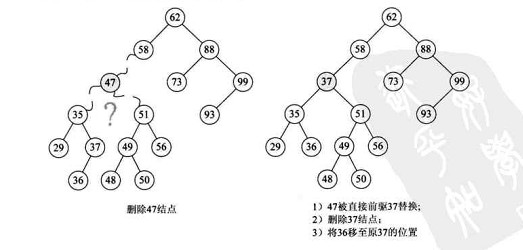
c. 左右子树都有的节点。( 用删除节点的直接前驱或者直接后继来替换当前节点,调整直接前驱或者直接后继的位置)
代码如下:
- int DeleteBST(BiTree *T, int key)
- {
- /* 若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素节点 */
- /* 并返回TRUE;否则返回FALSE */
- if( !(*T))
- return FALSE; /* 不存在关键字等于key的数据元素 */
- else
- {
- if( key == (*T)->data )
- Delete(T);
- else if( key < (*T)->data)
- return DeleteBST(&(*T)->lchild, key);
- else
- return DeleteBST(&(*T)->rchild, key);
- }
- }
- int Delete(BiTree *p)
- {
- /* 从二叉排序树中删除节点p, 并重接它的左或右子树 */
- BiTree q, s;
- if( !(*p)->lchild && !(*p)->rchild ) /* p为叶子节点 */
- *p = NULL;
- else if( !(*p)->lchild ) /* 左子树为空,重接右子树 */
- {
- q = *p;
- *p = (*p)->rchild;
- free(q);
- }
- else if( !(*p)->rchild ) /* 右子树为空,重接左子树 */
- {
- q = *p;
- *p = (*p)->lchild;
- free(q);
- }
- else /* 左右子树均不为空 */
- {
- q = *p;
- s = (*p)->lchild;
- while(s->rchild) /* 转左,然后向右走到尽头*/
- {
- q = s;
- s = s->rchild;
- }
- (*p)->data = s->data;
- if( q != *p ) /* 判断是否执行上述while循环 */
- q->rchild = s->lchild; /* 执行上述while循环,重接右子树 */
- else
- q->lchild = s->lchild; /* 未执行上述while循环,重接左子树 */
- free(s);
- }
- return TRUE;
- }
总结:二叉树以链式方式存储,保持了链接存储结构在执行插入或删除操作时不用移动元素的优点,只要找到合适的插入和删除位置后,仅需要修改链接指针节课。插入删除的时间性能比较好。而丢与二拆排序树的查找,走的就是从根节点到要查找的节点的路径,其比较次数等于给定值的节点在二叉排序树的层数。极端情况,最少为1次,即根节点就是要找的节点,最多也不会超过树的深度。也就是说,二叉排序树的查找性能取决于二叉排序树的形状。可问题就在于,二叉排序树的形状是不确定的。
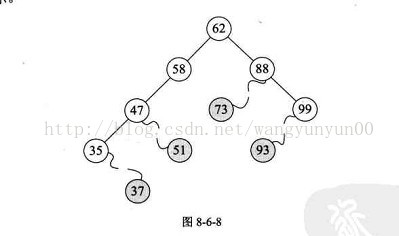
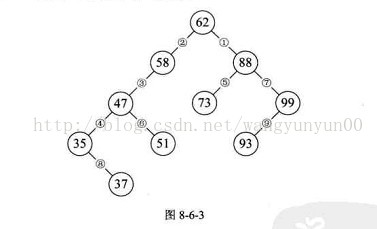
例如{62,88,58,47,35,73,51,99,37,93}这样的数组,我们可以构建一颗正常的二叉排序树。但是如果数组元素的次序是从小到大有序,如{35,37,47,51,58,62,73,88,93,99},则二拆排序树就成了极端的单支树,注意它依然是一颗二叉排序树。同样是查找节点99,左图只需要两次比较,而右图就需要10次比较才可以得到结果,而这差异很大。

也就是说,我们希望二叉排序树是比较平衡的,即其深度与完全二叉树相同。
这样就延续到了另一篇博客中要讲解的平衡二叉树。
附加:完整代码
- #include<stdio.h>
- #include<stdlib.h>
- #define TRUE 1
- #define FALSE 0
- /* 二叉排序树的节点结构定义 */
- typedef struct BiTNode
- {
- int data;
- struct BiTNode *lchild, *rchild;
- } BiTNode, *BiTree;
- int SearchBST( BiTree T, int key, BiTree f, BiTree *p )
- {
- /* 递归查找二叉排序树T中是否存在key */
- /* 指针f指向T的双亲,其初始调用值为NULL */
- /* 若查找成功,则指针p指向该数据元素节点,并返回TRUE */
- /* 否则指针p指向查找路径上访问的最后一个节点并返回FALSE */
- if( !T )
- {
- *p = f; //这是f唯一被用到的位置。
- return FALSE;
- }
- else
- {
- if( key == T->data )
- { *p = T; return TRUE; }
- else if( key > T->data )
- return SearchBST( T->rchild, key, T, p ); /* 在右子树继续查找 */
- else
- return SearchBST( T->lchild, key, T, p ); /* 在左子树继续查找 */
- }
- }
- int SearchBST2( BiTree T, int key, BiTree f, BiTree *p )
- {
- /*非递归*/
- BiTree s;
- if( !T )
- { *p = f; return FALSE; }
- else
- {
- while( T )
- {
- if( key == T->data )
- { *p = T; return TRUE; }
- if( key > T->data )
- { s = T; T = T->rchild; }
- else
- { s = T; T = T->lchild; }
- }
- *p = s;
- return FALSE;
- }
- }
- int InsertBST1( BiTree *T, int key )
- {
- /* 当二叉排序树T中不存在关键字等于key的数据元素时 */
- /* 插入key并返回TRUE,否则返回FALSE */
- /* 调用查找函数SearchBST,非递归 */
- BiTree p, s;
- if( !SearchBST2( *T, key, NULL, &p ) )
- {
- s = (BiTree)malloc(sizeof(BiTNode));
- s->data = key;
- s->lchild = s->rchild = NULL;
- if( !p )
- *T = s; /* 插入s为根节点,此前树为空树 */
- else if( key > p->data )
- p->rchild = s; /* 插入s为右孩子 */
- else
- p->lchild = s; /* 插入s为左孩子 */
- return TRUE;
- }
- return FALSE;
- }
- int InsertBST2( BiTree *T, int key )
- {
- /* 当二叉排序树T中不存在关键字等于key的数据元素时 */
- /* 插入key并返回TRUE,否则返回FALSE */
- /* 未调用查找函数,递归插入 */
- if( !(*T) ) /* 树为空, */
- {
- (*T) = (BiTree)malloc(sizeof(BiTNode)); /* 这个位置要留心,要重新分配空间,*T为空,说明未曾分配空间 */
- (*T)->data = key;
- (*T)->lchild = (*T)->rchild = NULL;
- return TRUE;
- }
- if( key == (*T)->data )
- return FALSE;
- if( key > (*T)->data )
- return InsertBST2( &((*T)->rchild), key ); /* 插入右孩子 */
- else
- return InsertBST2( &((*T)->lchild), key ); /* 插入左孩子 */
- }
- void order(BiTree t)//中序输出
- {
- if(t == NULL)
- return ;
- order(t->lchild);
- printf("%d ", t->data);
- order(t->rchild);
- }
- int DeleteBST(BiTree *T, int key)
- {
- /* 若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素节点 */
- /* 并返回TRUE;否则返回FALSE */
- if( !(*T))
- return FALSE; /* 不存在关键字等于key的数据元素 */
- else
- {
- if( key == (*T)->data )
- Delete(T);
- else if( key < (*T)->data)
- return DeleteBST(&(*T)->lchild, key);
- else
- return DeleteBST(&(*T)->rchild, key);
- }
- }
- int Delete(BiTree *p)
- {
- /* 从二叉排序树中删除节点p, 并重接它的左或右子树 */
- BiTree q, s;
- if( !(*p)->lchild && !(*p)->rchild ) /* p为叶子节点 */
- *p = NULL;
- else if( !(*p)->lchild ) /* 左子树为空,重接右子树 */
- {
- q = *p;
- *p = (*p)->rchild;
- free(q);
- }
- else if( !(*p)->rchild ) /* 右子树为空,重接左子树 */
- {
- q = *p;
- *p = (*p)->lchild; /* 不太理解 */
- free(q);
- }
- else /* 左右子树均不为空 */
- {
- q = *p;
- s = (*p)->lchild;
- while(s->rchild) /* 转左,然后向右走到尽头*/
- {
- q = s;
- s = s->rchild;
- }
- (*p)->data = s->data;
- if( q != *p ) /* 判断是否执行上述while循环 */
- q->rchild = s->lchild; /* 执行上述while循环,重接右子树 */
- else
- q->lchild = s->lchild; /* 未执行上述while循环,重接左子树 */
- free(s);
- }
- return TRUE;
- }
- void main()
- {
- int i;
- int a[10] = {62,88,58,47,35,73,51,99,37,93};
- BiTree T = NULL;
- for( i = 0; i < 10; i++ )
- InsertBST1(&T, a[i]);
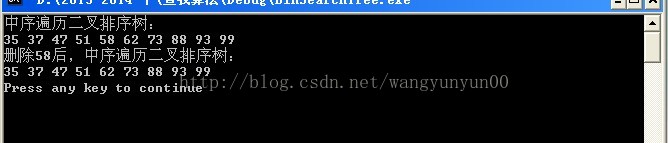
- printf("中序遍历二叉排序树:\n");
- order(T);
- printf("\n");
- printf("删除58后,中序遍历二叉排序树:\n");
- DeleteBST(&T,58);
- order(T);
- printf("\n");
- }
原文:http://blog.csdn.net/wangyunyun00/article/details/23708055






















 325
325

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








