排序概念总结及算法分类:
| 排序概念 | 排序是使得一个序列成为按关键字有序的序列的操作 |
| 排序稳定性 | 排序过程中排序前顺序和排序中不变的是稳定排序。 |
| 内排序和外排序 | 指待排序所有记录是否在内存中操作。外排序是排序记录态度要在内外存之间多次交换。(内排序:插入、交换、选择和归并) |
| 基于比较的排序 | 通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。主要算法有交换(冒泡、快速)、选择(简单选择、堆)、插入(简单插入、希尔排序)、归并(二路、多路归并)。 |
| 基于非比较排序 | 不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。主要有计数、桶。 |
1、冒泡排序:
| 原理理念 | 通过连续地比较与交换相邻元素实现排序,这个过程就像气泡从底部升到顶部一样,因此叫冒泡排序。 | |
| 算法特性 |
时间复杂度 | |
| 空间复杂度 | O(1) 原地排序:只需要常数的额外空间来交换数据。 | |
| 稳定排序 | 在“冒泡”中遇到相等元素不交换,原有的顺序不会改变。 | |
图解:
code 实现:
void bubbleSort(int arr[], int size)
{
for (int i = 0; i < size - 1; ++i)
{
bool swaped = false;
for (int j = 0; j < size - i - 1; ++j)
{
if (arr[j] > arr[j + 1])
{
swap(arr[j], arr[j + 1]);
swaped = true;
}
}
if (!swaped)//有数据交换说明已经有序
break;
}
}
2、简单选择排序:
| 原理理念 | 每次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到所有元素均排序完毕。 | |
| 算法特性 |
时间复杂度 | |
| 空间复杂度 | O(1) 原地排序:只需要常数的额外空间来交换数据。 | |
| 非稳定排序 | 选出最小的交换,被交换的元素到达的位置可能会改变相同元素的相对顺序 | |
图解: 
code 实现:
void selectSort(int arr[], int size)
{
for (int i = 0; i < size - 1; ++i)
{
int minIndex =i;
for (int j = i+1; j < size ; ++j)
{
if (arr[j] < arr[minIndex ])
{
minIndex =j;
}
}
swap(arr[minIndex], arr[i]);
}
}
3、插入排序:
| 原理理念 | 将一个记录插入到已经排好序的有序表中,从而一个新的记录数增 1 的有序表(整理扑克) | |
| 算法特性 |
时间复杂度 | |
| 空间复杂度 | O(1) 原地排序:只需要常数的额外空间来交换数据。 | |
| 稳定排序 | 在插入操作过程中,会将元素插入到相等元素的右侧,不会改变它们的顺序 | |
图解:
code 实现:
void InsertSort(int arr[], int size)
{
for (int i = 0; i < size; ++i){
for (int j = i; j >0&&arr[j]<arr[j-1]; --j)
{
swap(arr[j], arr[j - 1]);
}
}
}
4、希尔排序:
| 原理理念 | 它是插入排序的改进版,希尔排序又叫缩小增量排序,先将整个待排序列分割成若干子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后逐渐缩小增量,直至为1,最后使用直接插入排序进行最终排序。 | |
| 算法特性 |
时间复杂度 | 希尔排序的时间复杂度为O(n log n),但在最坏情况下的时间复杂度为O(n^2)。希尔排序通常比O(n^2)复杂度的算法快得多。 |
| 空间复杂度 | O(1) 原地排序:只需要常数的额外空间来交换数据。 | |
| 非稳定排序 | 相等的元素在排序后可能会改变它们的相对顺序 | |
图解:
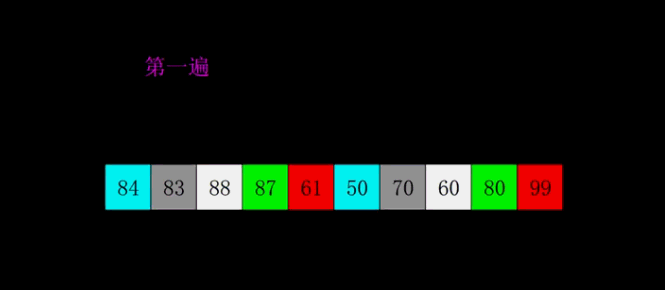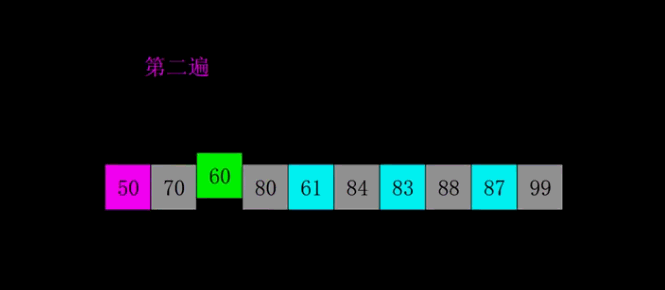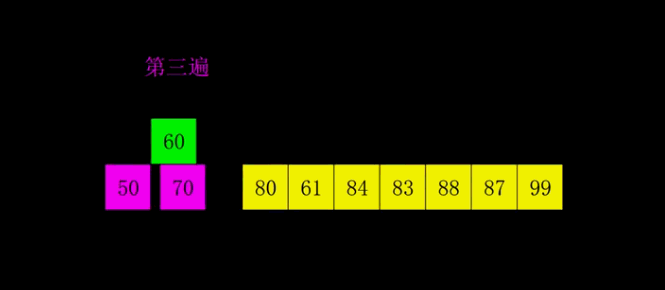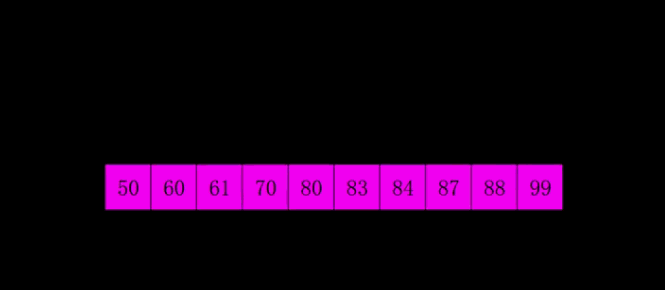
code实现:
void shellSort(int arr[], int size) {
// 从一个大的gap开始,然后在每次迭代中将gap减少一半
for (int gap = size / 2; gap > 0; gap /= 2) {
// 对每个gap进行插入排序
for (int i = gap; i < size; i++) {
int temp = arr[i];
for (int j = i; j >= gap && arr[j - gap] > arr[j]; j -= gap) {
swap(arr[j], arr[j - gap]);
}
}
}
}
5、归并排序:
| 原理理念 |
是一种基于分治策略的排序算法,分治:通过递归不断地将待排序从中点处分开,将长原序列分为子序列排序问题。合并:当子序列长度为 1 时终止划分开始合并,持续地将左右两个较短的有序数列合并为一个较长的有序数列,直至结束。 | |
| 算法特性 |
时间复杂度 | 归并排序的总体时间复杂度为O(nlogn),这是所有基于元素比较的排序算法中可达到的最优复杂度。在处理大规模数据时表现出色具有较高的效率。 |
| 空间复杂度 | O(n):元素需暂时在另一个序列中排序,序列的大小等于两个子序列的总长度 | |
| 稳定排序 | 相等的元素在排序后不会改变它们的相对顺序 | |
图解
code 实现:
void mergeSort(int arr[], int left, int right, int temp[])
{
if (left + 1 >= right)
return;
int mid = left + (right - left) / 2;
mergeSort(arr, left, mid, temp);
mergeSort(arr, mid, right, temp);
int p = left, q = mid, i = left;
while (p < mid || q < right)
{
if (q >= right || (p < mid && arr[p] <= arr[q]))
{
temp[i++] = arr[p++];
}
else
{
temp[i++] = arr[q++];
}
}
for (i = left; i < right; ++i)
{
arr[i] = temp[i];
}
}
6、堆排序:
| 原理理念 | 基于堆数据结构实现的高效排序算法。将待排序序列构建成一个大顶堆,序列最大值就是堆顶元素,将它移走(就是将其与序列末尾元素交换,最大值就确定了)将n-1序列重新构建一个堆,得到次小值,反复“建堆操作”和“元素出堆操作”实现堆排序。 | |
| 算法特性 |
时间复杂度 | 建堆操作使用 O(n) 时间。从堆中提取最大元素的时间复杂度为 O(logn) ,共循环 n−1 轮。它的最坏,最好和平均性能时间复杂度都是O(nlogn) |
| 空间复杂度 | 变量使用 O(1) 空间。元素交换和堆化操作都是在原数组上进行的。 | |
| 非稳定排序 | 在交换堆顶元素和堆底元素时,相等元素的相对位置可能发生变化。 | |
图解:
堆排序利用了大根堆(或小根堆)堆顶记录的关键字最大(或最小)这一特征,使得在当前无序区中选取最大(或最小)关键字的记录变得简单。(2)大根堆排序算法的基本操作:① 初始化操作:将R[1..n]构造为初始堆。②每一趟排序的基本操作:将当前无序区的堆顶记录R[1]和该区间的最后一个记录交换,然后将新的无序区调整为堆(亦称重建堆)。

code 实现:
/* 堆化 */
void siftDown(vector<int> &nums, int n, int i) {
while (true) {
// 判断节点 i, left, right 中值最大的节点,记为 max
int left = 2 * i + 1;
int right = 2 * i + 2;
int max = i;
if (left < n && nums[left] > nums[max])
max = left;
if (right < n && nums[right] > nums[max])
max = right;
// 若节点 i 最大或索引 left, right 越界则无须继续堆化跳出
if (max == i) {
break;
}
swap(nums[i], nums[max]); // 循环向下堆化
i = max;
}
}
/* 堆排序 */
void heapSort(vector<int> &nums) {
// 建堆操作:堆化除叶节点以外的其他所有节点
for (int i = nums.size() / 2 - 1; i >= 0; --i) {
siftDown(nums, nums.size(), i);
}
// 从堆中提取最大元素,循环 n-1 轮
for (int i = nums.size() - 1; i > 0; --i) {
swap(nums[0], nums[i]);
// 以根节点为起点,从顶至底进行堆化
siftDown(nums, i, 0);
}
}
7、快速排序:
| 原理理念 |
是一种基于分治策略的算法,快速排序的核心操作是“哨兵划分”,其目标是:选择数组中的某个元素作为“基准数”,将所有小于基准数的元素移到其左侧,而大于基准数的元素移到其右侧 | |
| 算法特性 |
时间复杂度 |
在平均情况下O(nlogn) 时间。在最差情况下,每轮哨兵划分操作都将长度为 n 的数组划分为长度为 0 和 n−1 的两个子数组,此时递归层数达到 n ,每层中的循环数为 n ,总体使用 O(n2) 时间。 |
| 空间复杂度 | 变量使用 O(n) 空间。在输入数组完全倒序的情况下,达到最差递归深度n,使用 O(n) 栈帧空间。排序操作是在原数组上进行的,未借助额外数组。 | |
| 非稳定排序 | 在哨兵划分的最后一步,基准数可能会被交换至相等元素的右侧 | |
图解:
code实现:
void quick_sort(vector<int> &nums, int l, int r)
{
if (l + 1 >= r)
{
return;
}
int first = l, last = r - 1, key = nums[first];
while (first < last)
{
while (first < last && nums[last] >= key)
{
--last;
}
nums[first] = nums[last];
while (first < last && nums[first] <= key)
{
++first;
}
nums[last] = nums[first];
}
nums[first] = key;
quick_sort(nums, l, first);
quick_sort(nums, first + 1, r);
}
8、计数排序:
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
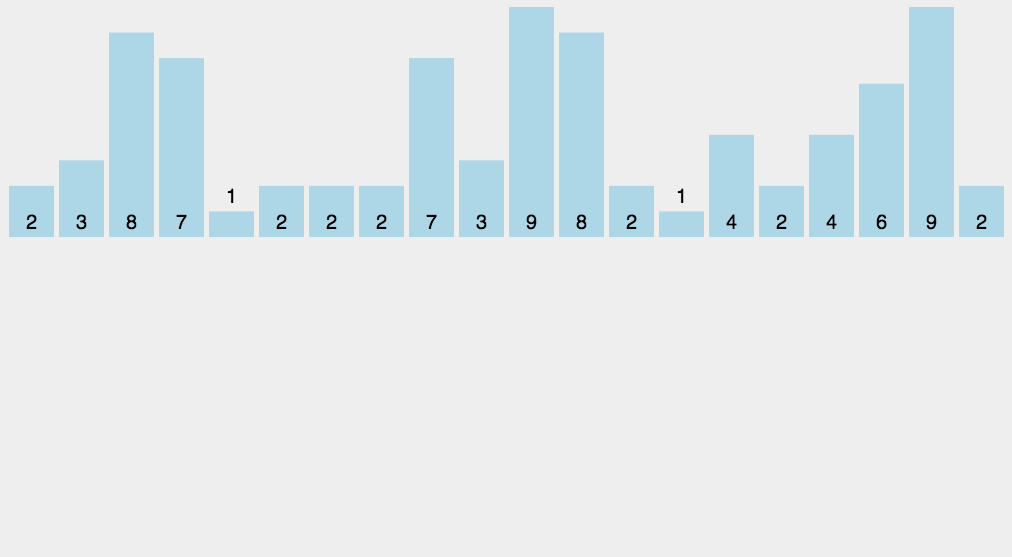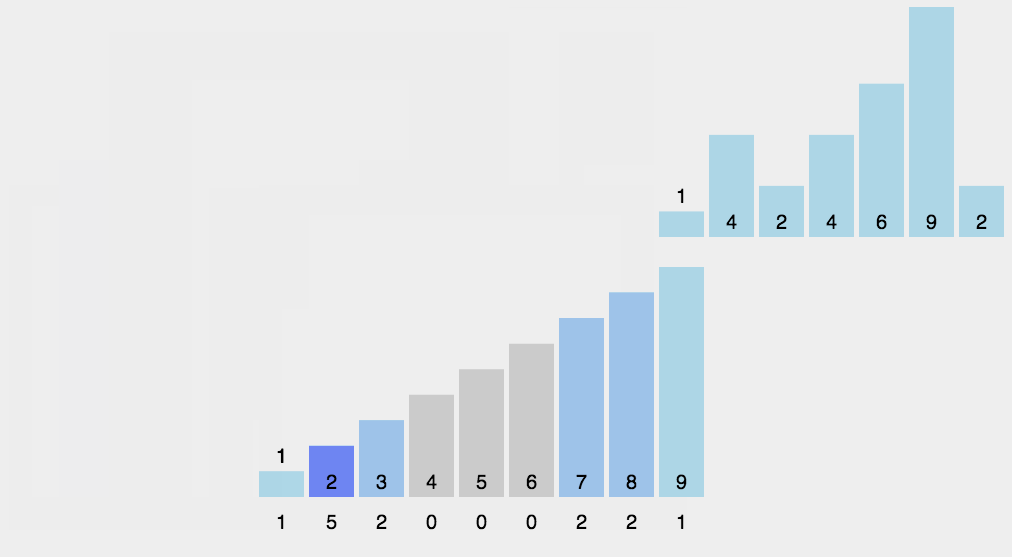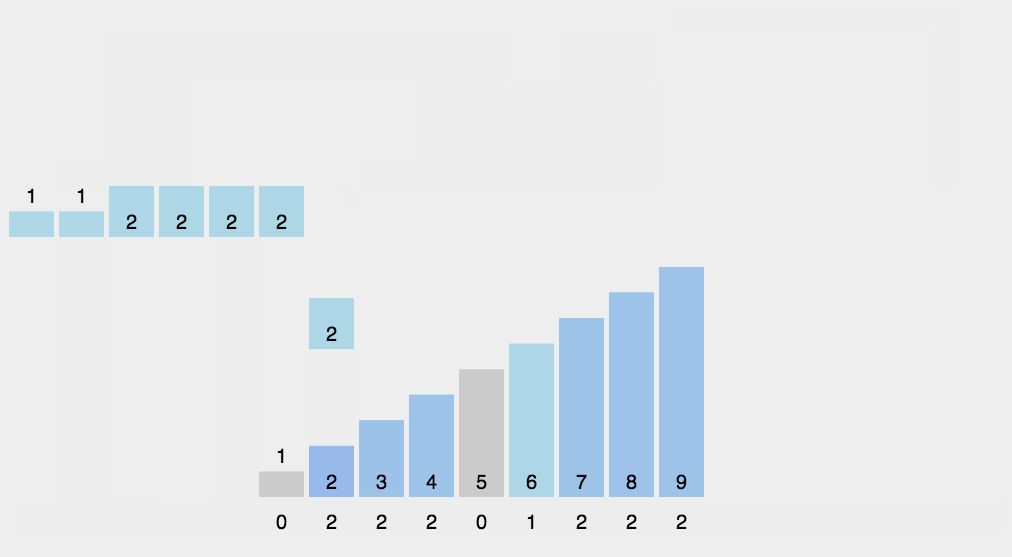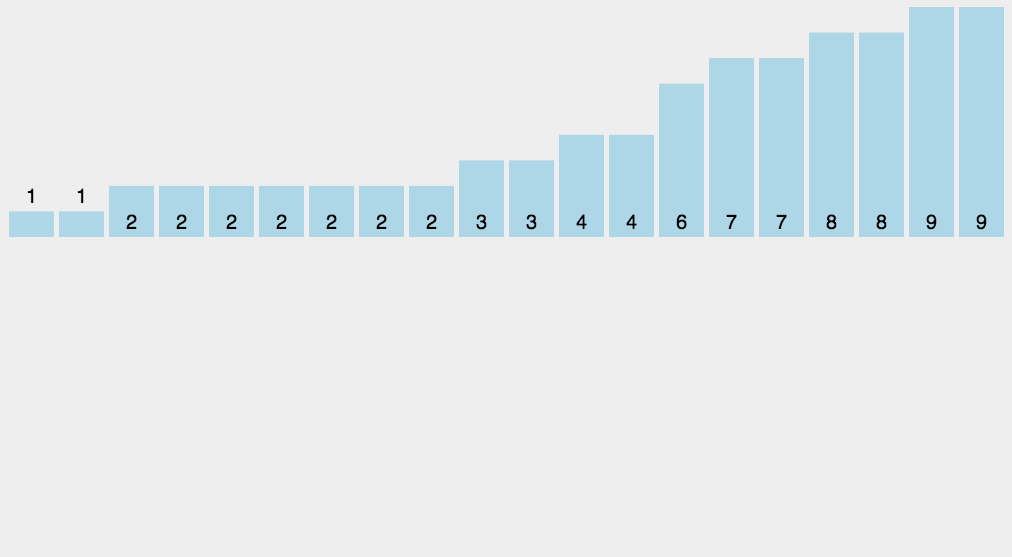
private static int[] countSort(int[] array,int k)
{
int[] C=new int[k+1];//构造C数组
int length=array.length,sum=0;//获取A数组大小用于构造B数组
int[] B=new int[length];//构造B数组
for(int i=0;i<length;i++)
{
C[array[i]]+=1;// 统计A中各元素个数存入C数组
}
for(int i=0;i<k+1;i++)//修改C数组
{
sum+=C[i];
C[i]=sum;
}
for(int i=length-1;i>=0;i--)
{
B[C[array[i]]-1]=array[i];//将A中该元素放到排序后数组B中指定的位置
C[array[i]]--;//将C中该元素-1,方便存放下一个同样大小的元素
}
return B;//将排序好的数组返回完成排序
}
return arr;
}
计数排序是一个稳定的排序算法。当输入的元素是 n 个 0到 k 之间的整数时,时间复杂度是O(n+k),空间复杂度也是O(n+k),其排序速度快于任何比较排序算法。当k不是很大并且序列比较集中时,计数排序是一个很有效的排序算法。
9、桶排序:
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。桶排序 (Bucket sort)的工作的原理:假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序(有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排)。
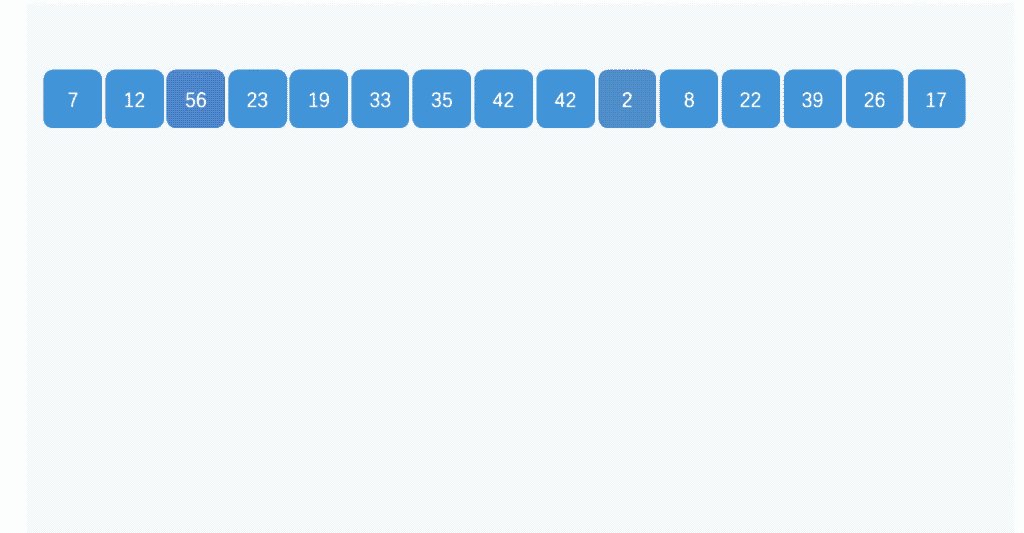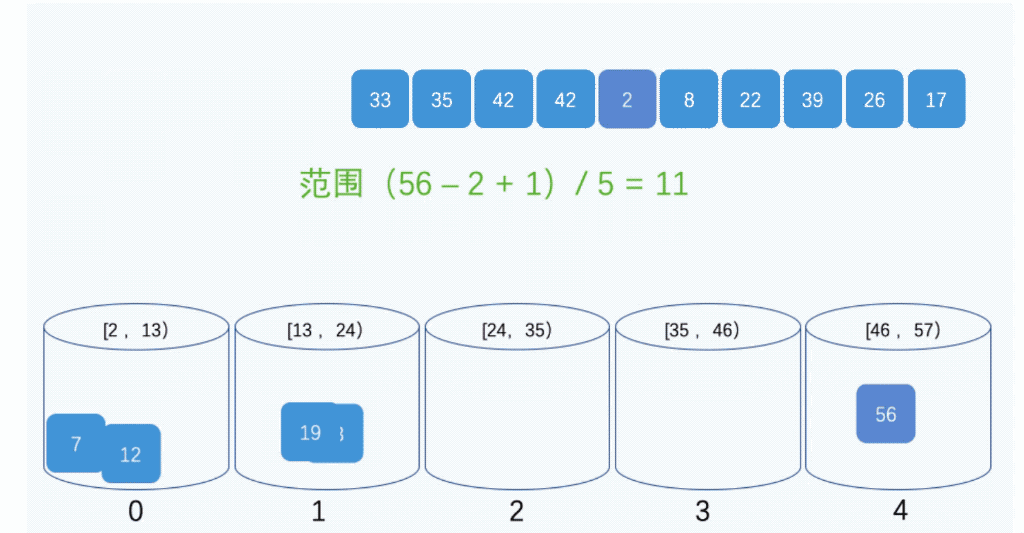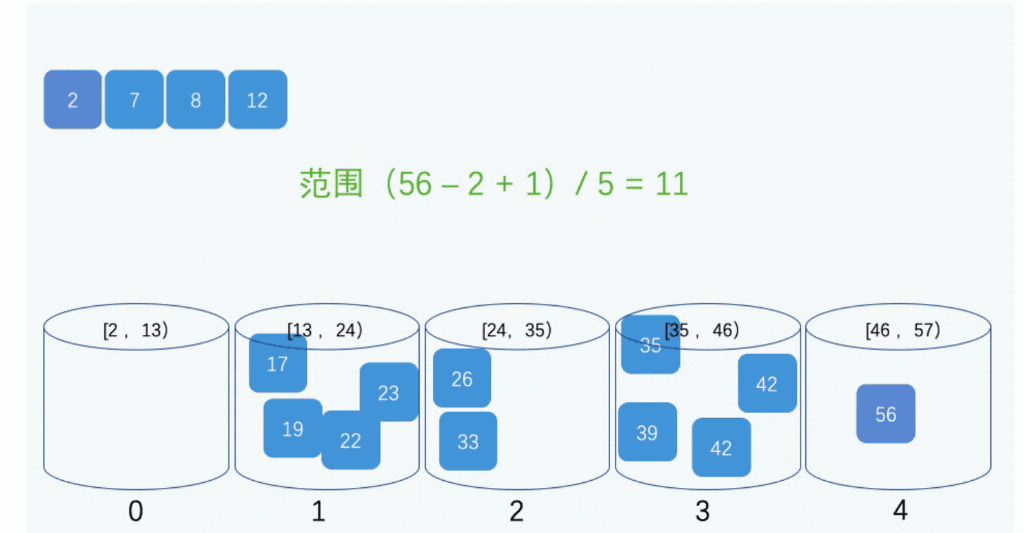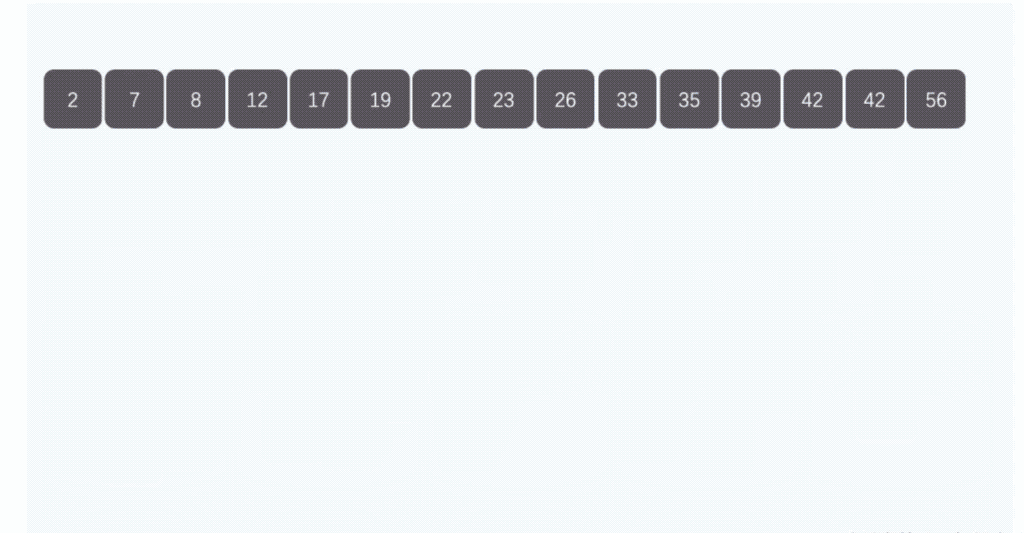
public static void bucketSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
//桶数
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
//将每个元素放入桶
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));
}
System.out.println(bucketArr.toString());
}
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
10、基数排序:
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。1) 取得数组中的最大数,并取得位数;2)arr为原始数组,从最低位开始取每个位组成radix数组;3)对radix进行计数排序(利用计数排序适用于小范围数的特点)

public class RadixSort {
private static void radixSort(int[] arr) {
//待排序列最大值
int max = arr[0];
int exp;//指数
//计算最大值
for (int anArr : arr) {
if (anArr > max) {
max = anArr;
}
}
//从个位开始,对数组进行排序
for (exp = 1; max / exp > 0; exp *= 10) {
//存储待排元素的临时数组
int[] temp = new int[arr.length];
//分桶个数
int[] buckets = new int[10];
//将数据出现的次数存储在buckets中
for (int value : arr) {
//(value / exp) % 10 :value的最底位(个位)
buckets[(value / exp) % 10]++;
}
//更改buckets[i],
for (int i = 1; i < 10; i++) {
buckets[i] += buckets[i - 1];
}
//将数据存储到临时数组temp中
for (int i = arr.length - 1; i >= 0; i--) {
temp[buckets[(arr[i] / exp) % 10] - 1] = arr[i];
buckets[(arr[i] / exp) % 10]--;
}
//将有序元素temp赋给arr
System.arraycopy(temp, 0, arr, 0, arr.length);
}
}
}
基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的。基数排序的空间复杂度为O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右。
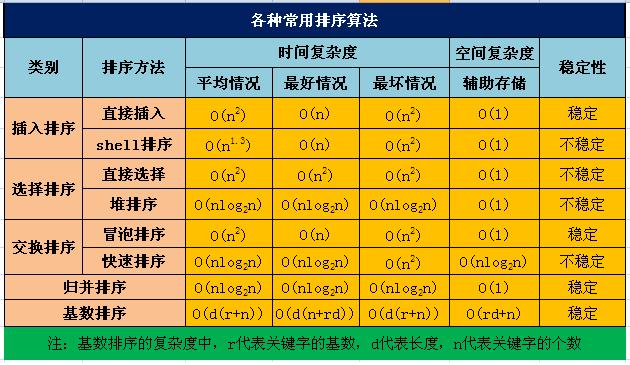
各排序算法的性能对比






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








