Alpha-expansion and Alpha-beta-swap Algorithm Flow

简介

主题：采用图割方法解决视觉问题中常见的能量最小化问题 
主要参考文献：Fast Approximate Energy Minimization via Graph Cuts， Cornell University, Boykov, Veksler, Zabih, IEEE PAMI 23(11), pp 1222ff, 2001 
在诸多视觉图像问题中，研究人员最后都能将其归结为最小化一个能量函数的问题，很多文献中都引用这篇文章：Fast Approximate Energy Minimization via Graph Cuts，该文章在 google scholar 上显示截至目前引用超过5k+。该文章中介绍了两种采用图割来解决能量最小化问题的算法：  α -expansion and  α - β  swap algorithms。 
下面本文通过拜读并翻译原文，加上个人理解试着弄清楚这两个算法的来龙去脉，如有错误敬请指出。

计算机视觉中的能量最小化问题描述

在计算机视觉领域中，我们经常需要估计一些在空间（像素平面）上变化的量，例如图像灰度、视差大小等。这些量都有着共同的特征：分块平滑（piecewise smoothness）。分块平滑意味着两个方面：这些量在块的内部变化平滑，在块与块之间（物体边界）变化很大。对每一个像素点  p∈P  我们都需要给定一个标签（label） fp∈L ，也就是将每个像素映射到标签集中的某个标签上，这里标签函数（映射）  f  不仅需要满足分块平滑的特点而且需要和观测到的数据一致。 
基于以上想法，这些视觉问题就可以表达成以下寻找标签函数  f  以求能量最小化的形式： 

E(f)=Esmooth(f)+Edata(f),

在这里  Esmooth(f)  表达的是  f  分块不平滑的程度， Edata(f)  表达的是标签函数  f  与观测到数据的不一致性。 Edata(f)  的一般形式是： 

Edata(f)=∑p∈PDp(fp),

其中  Dp  来度量标签与观测数据的一致性，例如在图像恢复中  Dp(fp)=(fp−ip)2  ，其中  ip  表示在像素点  p  处的灰度值，在这里  Edata(f)  并不是重点。 
平滑项  Esmooth  才是关键所在 。为了在边界处得到较好的效果，我们选择一种“非连续性保留”(discontinuity-preserving) 函数（参考分块平滑两项性质）。 
由于能量最小化是非凸优化问题，具有很多局部极小值，并且解空间有  |P|  维，因此解这种能量最小化问题最大的障碍就是巨大的搜索空间。模拟退化法可以优化任意能量函数，但是通常计算非常缓慢。 
在这篇文章中主要考虑的平滑项具有以下形式： 

Esmooth=∑{p,q}∈NVp,q(fp,fq),

这里  N  表示的是相邻的像素对集合。 Vp,q(fp,fq)  表示像素对  {p,q}  在标签函数  f  下生成的标签  (fp,fq)  之间的距离（相似度、平滑程度）。在某些特殊情况下这种能量形式是能够精确的最优化，这里不展开，一般来说，这个问题是 NP 难问题。 
该论文中提出了两种对任意有限大小的标签集  L  进行近似能量最小化的算法： α -expansion and  α - β  swap，分别针对两种互作用势（interaction potentials）：度量（metric）、半度量（semi-metric）。 V  在标签空间  L  上满足下面两个条件时才称之为半度量：对任意一对标签  α,β∈L  ，都有  V(α,β)=V(β,α)≥0  和  V(α,β)=0⇔α=β.  如果  V  对任意的  α,β,γ∈L  还满足三角不等式： 

V(α,β)≤V(α,γ)+V(γ,β)

那么我们就称  V  是度量的。需要注意的是不论是度量还是半度量互作用势，都包含重要的“非连续性保留”的互作用势。这个特性在后续证明中是会用到的，也说明了两种算法分别适用的情况。

采用图割来最小化能量

对所面临的问题进行了简单的形式化的描述后，我们下面就会采用一种图割的方法来求解这个问题。总体思路是每一次 expansion（swap）调整一（两）个标签来使得能量函数下降，遍历所有标签（组合）直至能量函数在所有的一次 expansion（swap）调整标签中不能下降，算法停止，达到局部最优。

分割和移动空间

每一个标签映射函数  fp∈L  与图像分割方式是一一对应的关系，而  fp （后简写为  f ） 是能量函数的自变量，因此我们可以称所有可能的  f  的取值所组成的集合为操作空间或移动空间，用数学描述如下： 
任意一种标签方式  f  都能通过像素的一个分割来表示：  P={Pl|l∈L}  其中  Pl  表示标签为  l  的像素点集合。可以看到标签方式  f  与分割  P  成一一对应关系。 
每一次标签调整，也就是  f  在操作空间中的每一次移动遵循一定规定的我们称之为交换（ swap ）和扩张（ expansion ）操作， swap  和  expansion 操作的具体意义： 
-  swap : 给定一对标签  α,β ，从一个分割  P  到另一个分割  P′  的移动（变动）在满足以下条件时称之为一次  α - β swap  标签调整操作：对任意  l≠α,β  都有  Pl=P′l 。也就是说在一次  α - β swap  调整操作后，一些原来是  α  标签的像素被标记为  β ，一些原来是  β  标签的被标记为  α ，简而言之就是被标记为  α,β  标签的像素集合之间进行了交换，这也是该算法名称的由来。 
-  expansion : 给定一个标签  α ，从一个分割  P  到另一个分割  P′  的移动（变动）在满足以下条件时称之为一次  α - expansion  标签调整操作：对任意标签  l≠α  都有  P′l⊂Pl 。也就是说在一次  α - expansion  调整操作中，除了  α  标签以外的集合都是原来的子集，简而言之就是被标记为  α  标签的像素集合扩大了，这也是该算法名称的由来。 
上面定义了一次 expansion（swap）操作对象是具体的一（两）个标签集合，和操作规范，并没说明具体哪些像素进行扩张或交换操作。对不同的操作对象，必然产生截然不同的 expansion（swap）操作，相同的操作对象，对不同的像素操作，也是不同的 expansion（swap）操作。

算法流程和性质

上面定义了 expansion（swap）操作空间和每一次 expansion（swap）调整操作规范，算法总流程如下图： 
 
图中上部分是  swap  算法，下部分是  expansion  算法，可以看到两种算法基本结构相同：在 3 中遍历所有可能的标签调整对象，并对该调整对象具体调整方式寻求最优  f^ ，如果找到的当前调整对象的最优调整有效即：  E(f^)<E(f)  使得能量下降，则接受这个调整  f:=f^ 。对标签不断的进行调整，直到没有标签调整能使能量函数下降为止。 
两种算法区分就在对当前标签对象进行具体调整的方式 3.1 - 3.2 这两步上，两种标签调整方式在上一部分已经进行了说明。 
该文中的算法就是每一次在整个操作空间的一个有限的（ swap  or  expansion  操作对象所决定）子空间内寻找最优点并移动，直到在一次操作中对能量没有减小作用。此时得到的能量值是一个局部极小值，并不是全局极小值，有相关证明 expansion 算法得到的标记与全局最优成可控的倍数关系。

图割

上面只是给出了算法的框架流程，但具体解决算法的最关键步骤就是 3.1：在当前标签对象的一次  swap  或  expansion  调整中找到的最优标签方式  f^ ，这里我们通过图割的方法来有效的找到  f^ 。 
这里简单介绍下图割问题：给定一幅无向带边权图  G=⟨V,E⟩  并包含了两个特殊的节点，源节点 source，汇节点 sink。这幅图的一个割就是边集合  E 的一个子集  C⊂E  称为割集，使得在图中去除割边集合后源点和汇点不能联通，一个割的代价记为  |C|  就是割集中所有边权之和。 
最小割问题就是找到一个割使得代价最小。这是一个很成熟的问题，已经提出了不少低阶多项式复杂度的算法，例如 Ford-Fulkerson，Push-relabel，这些算法在实际中都是近乎线性复杂度。

找到最佳的 swap 移动

对于一个输入的标记方式  f （也即是分割方式  P ）和一对标签  α,β ，我们期望找到一个具体的标记方式  f^  使得总能量  E  在此时  f  上的  α - β  标签对的 swap 调整操作中最小。注意这里的最小是针对当前输入的标记方式  f  和  α - β  标签集上的一次 swap 操作而言的。 
这里采用构建图  Gαβ=⟨Vαβ,Eαβ⟩  并在图上解最小割问题的方式来找到当前  f  在标签对上  α - β  最佳 swap 调整。这个图的结构是由当前  f  和标签对 α - β  所决定的。

构建图

每次我们都是基于当前分割  f  和标签对  α - β  来构建图  Gαβ  的，在一维情形下： 
 
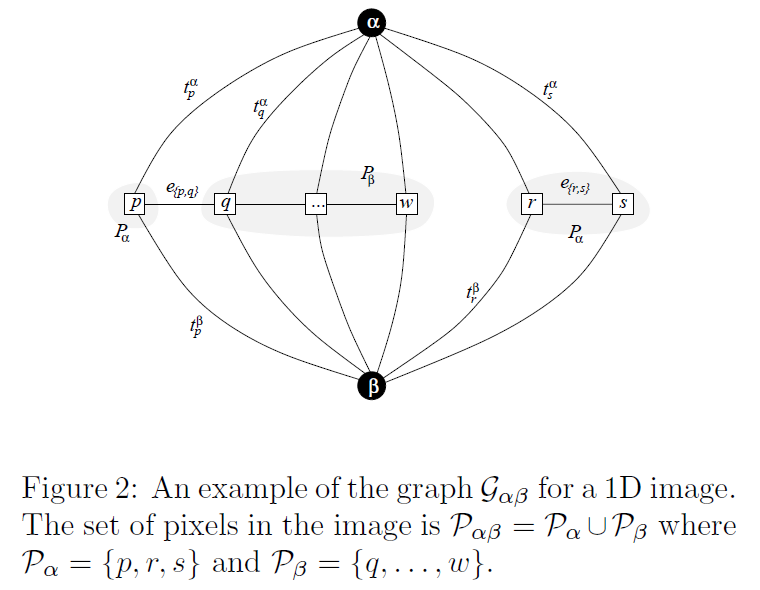
图中，顶点集合包含汇源节点  α,β  和像素点  p∈Pα∪Pβ ， p  与汇、源节点分别连接边，称之为  t - link ，每对相邻的像素点之间连接一条边，称之为  n - link ，我们用  {p,q}∈N  来表示两个像素相邻。那么图  Gαβ  的边集合 

Eαβ=⋃p∈αβ{tαp,tβp}∪⋃q∈Npp,q∈Pαβe{p,q}

每条边的权值： 

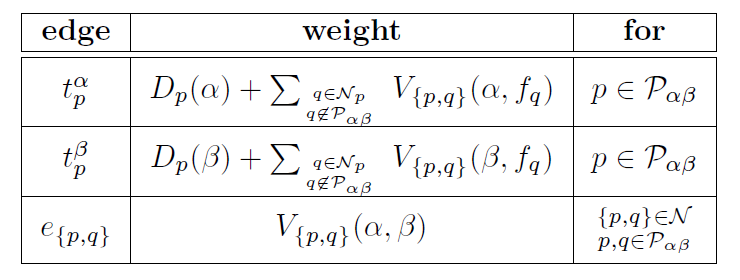
最小割与最佳 swap 移动

对于构造的图中的一个割有如下的几种情况： 
 
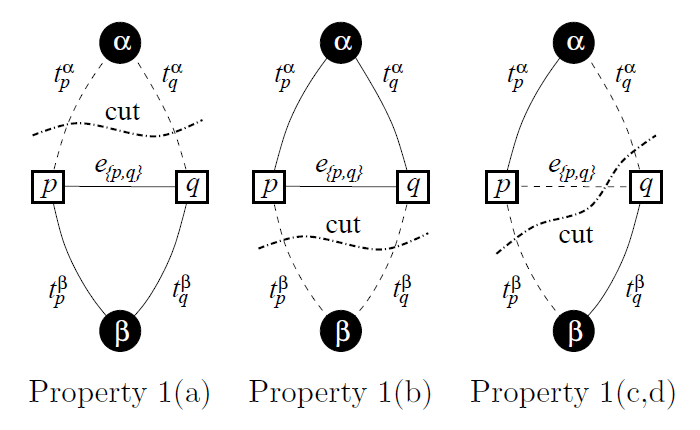
从图中可以看到每个像素顶点有且仅有一条t边在割集中（也意味着每个像素只能拥有一个标签），如果两个相邻的像素被标记为不同的标签，那么他们之间的n边也属于割集。有这样的观察我们可以得到以下两个引理： 
- Lemma 1: 与一个割  C  对应的整体标签函数  fC  与输入的标签函数  f  之间正好是一次  α - β  swap 的关系。 
- Lemma 2: 对于任意一个割  C  和任一n边  e{p,q}  都有： 

|C∩e{p,q}|=Vp,q(fCp,fCq).

因为割集与n边交集只有在两个不同标签交界处才会产生。由此得到： 
Theorem 1 : 图  Gαβ  上的一个割  C  与  f  上的一次  α - β  swap 成一一对应关系。并且，割的费用  |C|=E(fC)+constant 。证明如下： 
图  Gαβ  上的一个割的费用  |C|  有： 

|C|=∑p∈Pαβ|C∩{tαp,tβp}|+∑{p,q}∈N{p,q}⊂PαβV{p,q}(fp,fq).

对于前一项，割集与t边相交，结合权值表中的定义，我们有： 

|C∩{tαp,tβp}|=Dp(fCp)+∑q∈Npq∉PαβVp,q(fCp,fq).

后一项表示割集中的n边权值，结合 Lemma 2 可以得到： 

|C|=∑p∈PαβDp(fCp)+∑{p,q}∈Nporq∈PαβVp,q(fCp,fCq).

注意到前一项中产生的平滑项与后一项中的平滑项结合定义的平滑项对象是两个相邻像素且至少有一个属于  α−β  标签总计集合中。 
这时候我们就可以将割集代价写为： |C|=E(fC)−K ，其中  K  的值为： 

K=∑p∉PαβDp(fp)+∑{p,q}∈N{p,q}∩Pαβ=∅Vp,q(fCp,fCq).

这个数值对于当前  f  和标签对  α−β  的所有割  C  是完全一样的常数。那么必有推论： 
Corollary 1 :  f  的最佳  α - β  swap 是  f^=fC ，这里  C  是图  Gαβ  上的最小割。

找到最佳的 expansion 移动

对于一个输入的标记方式  f （也即是分割方式  P ）和一个标签  α ，我们期望找到一个具体的标记方式  f^  使得总能量  E  在此时  f  上的  α  标签的 expansion 调整操作中最小。 
这里采用构建图  Gα=⟨Vα,Eα⟩  并在图上求解最小割问题的方式来找到当前  f  对标签  α  的最佳 expansion 调整。图的结构是由当前  f  和标签  α  所决定的，并假设平滑项  V{p,q}  是度量的，也就是满足三角不等式。

构建图

每次我们都是基于当前分割  f  和标签  α  来构建图  Gαβ  的，在一维情形下： 
 
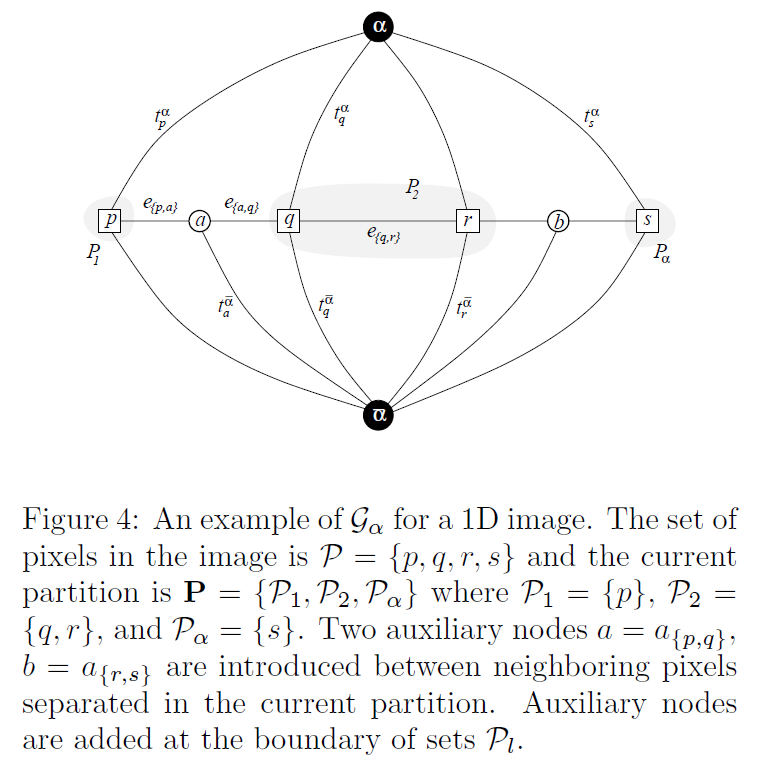
汇源节点分别代表标签  α  和其他标签  α¯ ，与上一算法的不同之处在于： 
- 图在整幅图像的所有像素点上构造， 
- 在相邻且具有不同标签顶点（ {p,q}∈Candfp≠fq ）间添加额外的辅助节点  a{p,q} ，也就是在分割边界上需要辅助节点， 
- 相应的对于辅助节点我们需要添加额外的三条辅助边，分别与两个边界点和  α¯  相连，并且在构造权重时使得他们之间满足三角不等式。 
所有边的集合及权重如下图： 

最小割与最佳 expansion 移动

与上一部分类似，每个像素顶点有且仅有一条t边在割集中，如果  tα¯p  边在割集中，那么该像素就保持原标签。同样我们可以得到： 
Lemmma 3:  Gα  的一个割与一次  f  上标签  α  的 expansion 移动一一对应。 
特别的，对于最小割我们有以下割边情形： 
 
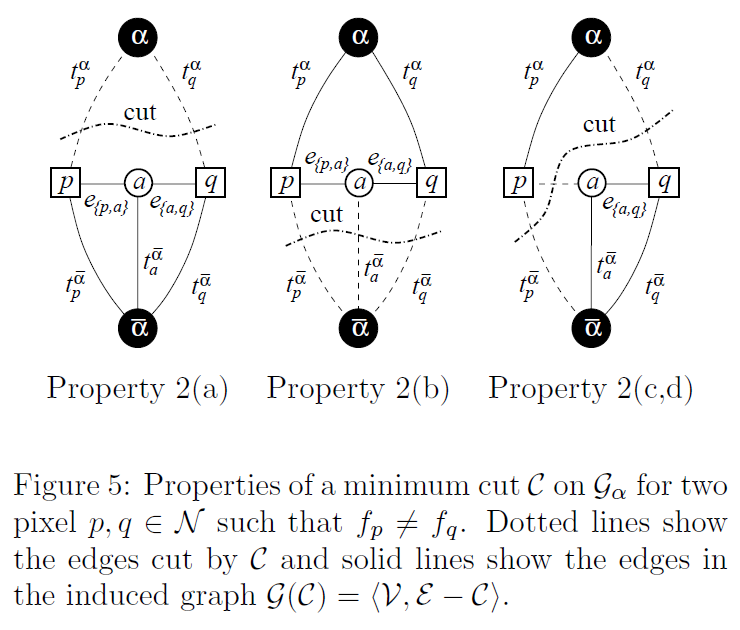
- 图中中间情形：当之前相邻边界像素保留原标签（ fa=α¯ ），那么由于中间的辅助节点三条边满足三角不等式，就必须切t边（ tα¯a ）。 
- 图中右边情形：当之前相邻边界像素其中一个变成  α  标签，另一个保留原标签，那么还是由于三角不等式， e{p,a}  必定包含在割集中。 
三角不等式在这里的意义就是尽量只切辅助节点的某一条边。 
与上一部分类似，通过之前定义的割边权值计算最小割代价可以证明  |C|=E(fC) 。那么有： 
Corollary 2: 从当前  f  和标签  α  出发的最佳  α  expansion  f^=fC ，其中  C  是图  Gα  上的最小割。

总结

整个系统的目的就是最小化能量  E ，我们控制的输入变量是标记函数  f 。算法就是在当前输入下找到下一步所能达到的最小值，然后移动，如此循环，直至下一步找不到更小的能量值了。 
Fast Approximate Energy Minimization via Graph Cuts 文中提出的两个算法都能同时改变大范围像素集的标号;而其它的标准算法一般用微小的移动，一次仅能改变一个像素的标号。 
算法可以类比于梯度下降法：在操作空间的每一个  f  点，存在很多的优化方向簇，每对（个）标签形成一个 swap（expansion） 优化方向簇，在一个优化方向簇中存在很多的优化方向也就是具体的哪些像素进行 swap（expansion），通过图割的方法我们找到并移动到当前最优点，检查下一个优化方向簇。最后算法在操作空间的某个点的所有优化方向簇内都找不到更好的移动点时，算法结束，得到一个可控的局部极小值。 
基本的图割方法一般用来解决两个标签的问题，而在这篇文章作者中通过巧妙的构造网络，每次进行两个标签— {α,β} ， {α,α¯}

 间的移动，漂亮地解决了问题。

原文链接：http://blog.csdn.net/nothinglefttosay/article/details/48554555