2020杭电:Fibonacci Sum(赛后补题，然而一直T，写思路)

本文探讨了斐波那契数列的高效求解方法，通过矩阵快速幂和阶乘逆元技巧，避免了传统递归的高时间复杂度。介绍了如何利用斐波那契数列的特殊性质，结合模运算优化算法，实现大数计算。

题意:F为斐波那契数列，求
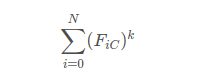
在这里插入图片描述
模1e9+9的值。

我也是赛后补题的，所以只是在大佬的方法基础上加一些较为基础的东西，虽然是借鉴了大佬的方法，但还是一直Tqaq，大佬说是因为比赛完换机子测了，所以过不了了。

先说下我比赛时的做法吧，比赛的时候我还不知道斐波那契数列还有其他通项公式，虽然就算知道也极有可能做不出来，所以我采用矩阵快速幂求解出每个Fic，然后再用一般的快速幂求Fic^k，然后毫无疑问的T了，太惨了。

好了，来看看大佬们的做法吧
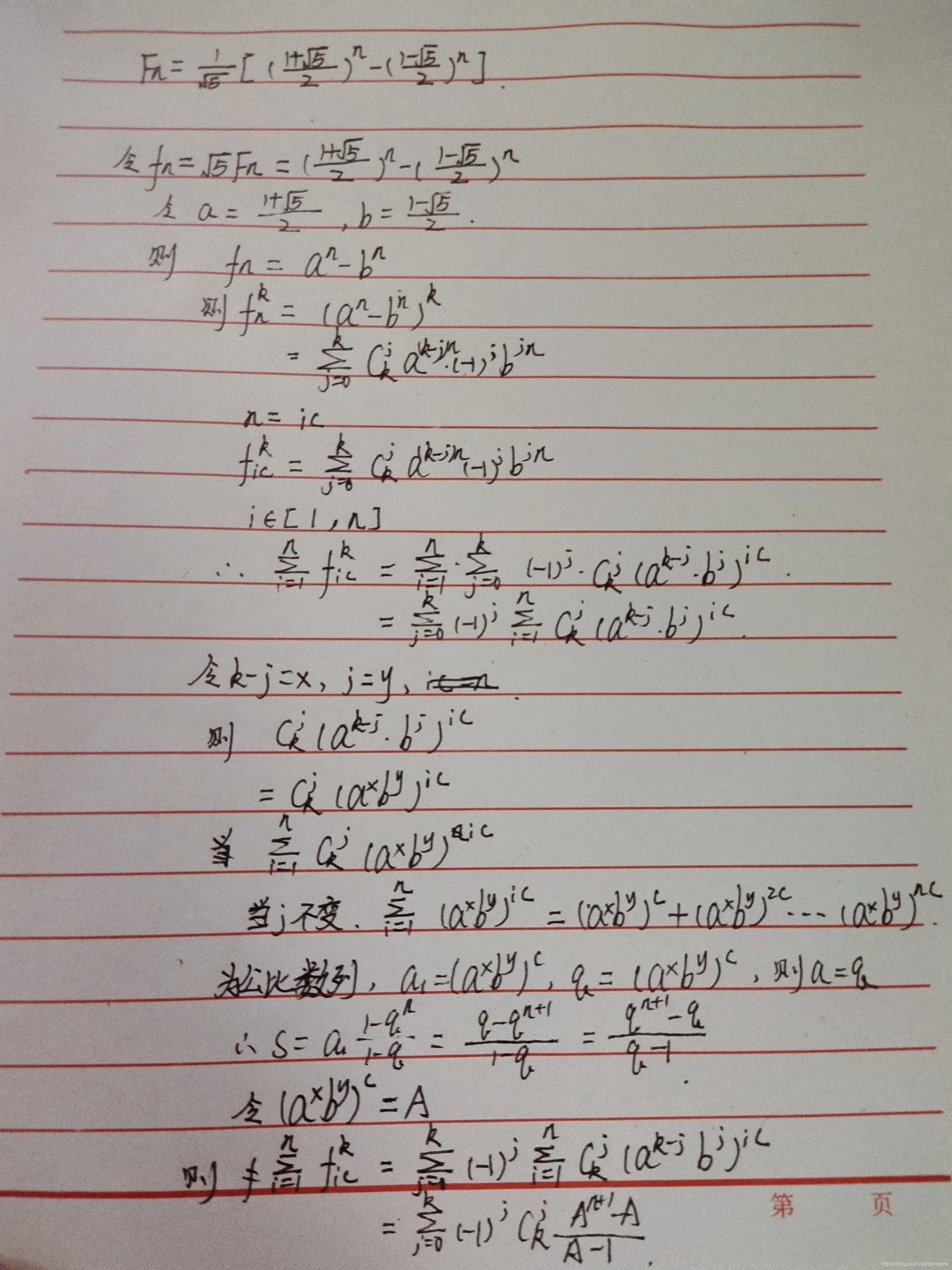
在这里插入图片描述
忘写了，上面应该还要乘以乘以5^(-k/2)
根据上面的最后推导结论来看看我们要求神马

求出5^(1/2)的逆元，设x为5^(1/2)的逆元，则有x²的逆元为5，先暴力求出，得到的结果为p = 383008016

a和b,即斐波那契通式的n次项

 A = (p + 1ll) * (mod + 1) / 2 % mod, B = (1ll + mod - p) * (mod + 1) / 2 % mod;//注意1-5^(-1/2)是小于0的

阶乘，记fc为阶乘，fcn为阶乘的逆元，则有C(k,j)=fc[k]*fcn[j]*fcn[k-j].
阶乘逆元求法:

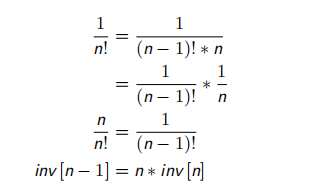
至于快速幂，我觉得就大家都会没必要贴了，就不贴了。