2025“钉耙编程”中国大学生算法设计春季联赛（5）1010-CSDN博客

比赛的时候定睛一看，哇塞树类型的题目，不用想要么链式前向星跑dfs或者数组跑dfs。

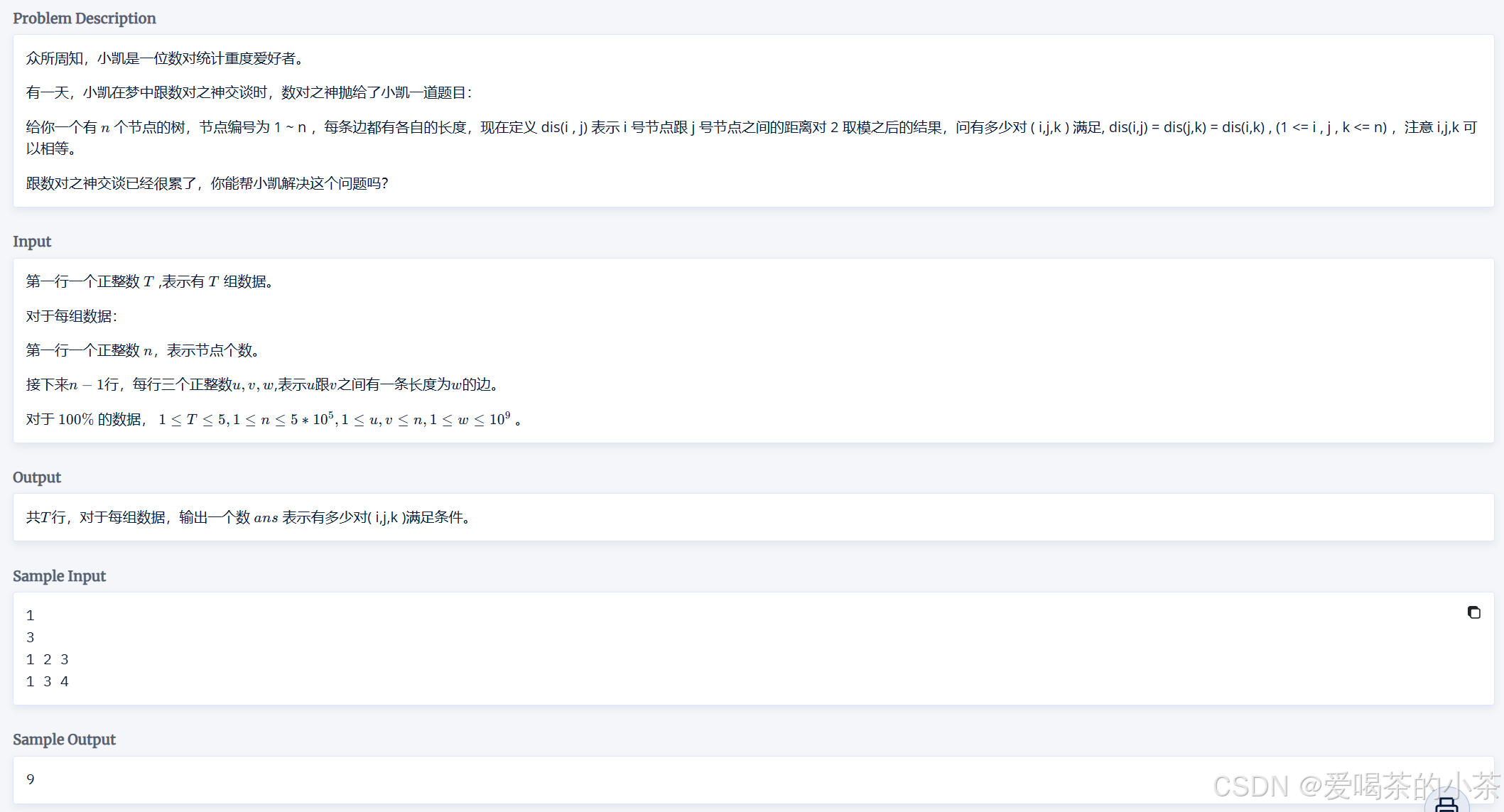
题目表达很清晰，求是否存在dis[i][j]=dis[j][k]+dis[i][k]，并统计个数。

由于dis[i][j]只有两种取法0,1，所以直接将所有两两之间距离为0的节点和距离为1的节点分别放入一个数组中，随后在集合中任意选择两个点之间的距离都为0，假定距离为0的集合大小为k那么答案的维护就是k*k*k（因为题目给定，可以重复选定同一个点），距离为1的集合答案同理。

#include <bits/stdc++.h>
using namespace std;
struct Edge {
    int to, val;
};
/*
void dfs(int u,int parent,int parity){
    cnt[parity]++;
    for(auto it:adj[u]){
        if(it!=parent){
            dfs(it.to,t,parity^(it.val%2));
        }
    }
    这里有一点不好的就是数组要开在全局中，T种数据下要不断地清空前数据
}
*/
void solve() {
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        vector<vector<Edge>> adj(n + 1);  // 邻接表，adj[1..n] 存储各节点的边
        for (int i = 1; i < n; i++) {
            int u, v, w;
            cin >> u >> v >> w;
            adj[u].push_back({v, w});
            adj[v].push_back({u, w});  // 无向图，双向加边
        }

        long long cnt[2] = {0, 0};  // cnt[0] 和 cnt[1] 分别统计两种情况的节点数

        function<void(int, int, int)> dfs = [&](int u, int parent, int parity) {
            cnt[parity]++;
            for (const Edge& e : adj[u]) {
                if (e.to != parent) {
                    //子节点不等于父亲节点直接往下递归
                    dfs(e.to, u, parity ^ (e.val % 2));  // 递归计算子节点
                }
            }
        };

        dfs(1, -1, 0);  // 从根节点 1 开始 DFS，初始 parity=0，一开始1的父亲节点是-1，更合理

        long long ans = cnt[0] * cnt[0] * cnt[0] + cnt[1] * cnt[1] * cnt[1];
        cout << ans << "\n";
    }
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    solve();
    return 0;
}

下面给一个链式前向星的代码，其实上下两个代码差不多，下面代码打起来会快一点点（应该是吧.....）

#include <bits/stdc++.h>
#define int long long
using namespace std;
struct Edge {
    int to, val;
};
int T, s[2], n, x, y, z;
vector<vector<Edge>> adj;
void dfs(int t, int fa, int opt) {
    ++s[opt];
    for (const auto& edge : adj[t]) {
        if (edge.to != fa) {
            dfs(edge.to, t, opt ^ (edge.val % 2));
        }
    }
}
signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> T;
    while (T--) {
        s[0] = s[1] = 0;
        cin >> n;
        adj.assign(n + 1, vector<Edge>());
        for (int i = 1; i < n; i++) {
            cin >> x >> y >> z;
            adj[x].push_back({y, z});
            adj[y].push_back({x, z});
        }
        dfs(1, 0, 0);
        cout << s[0] * s[0] * s[0] + s[1] * s[1] * s[1] << '\n';
    }
}