理解FEC（Reed-Solomon）编码

https://zhuanlan.zhihu.com/p/103888948 

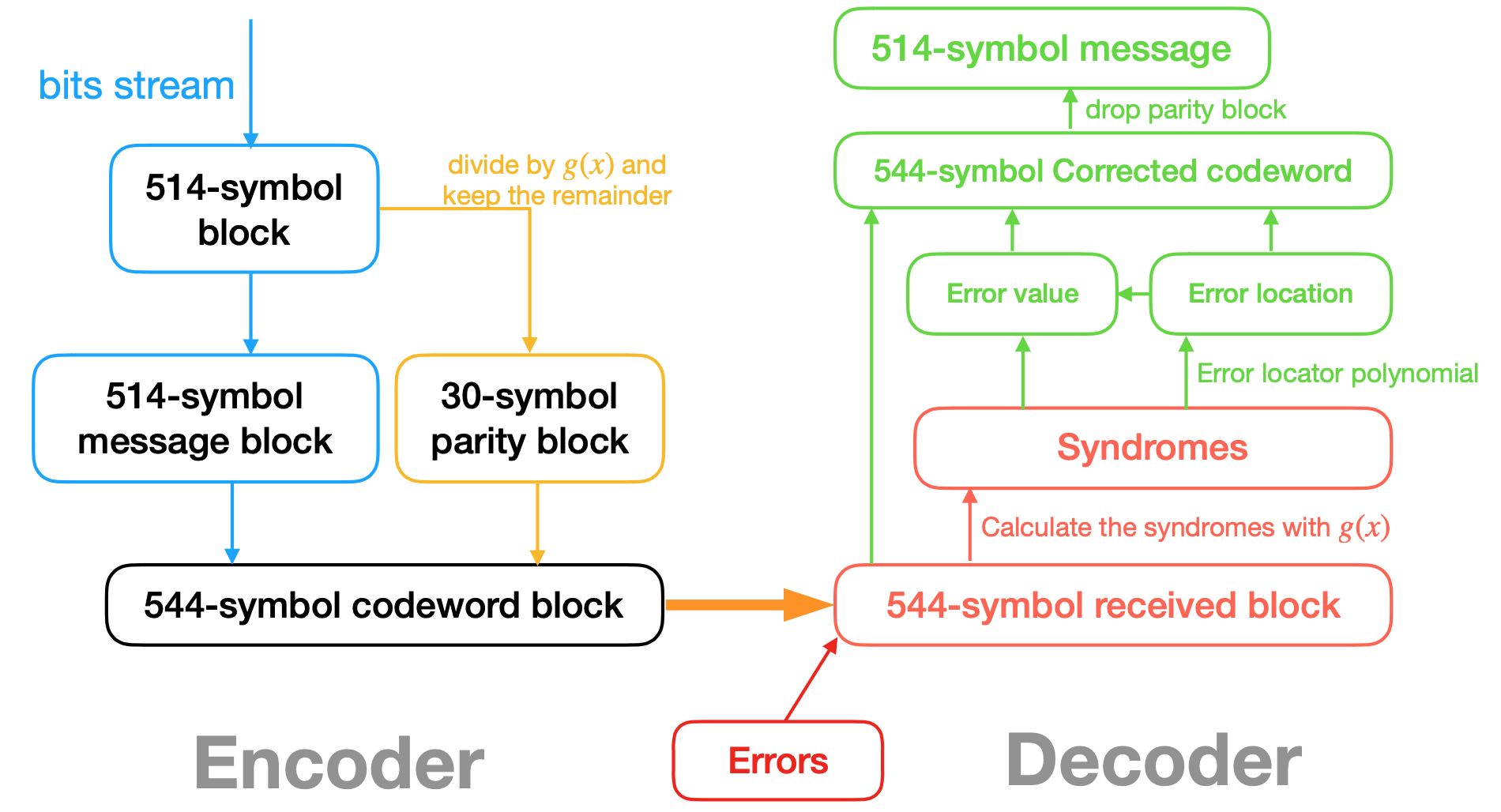
理解FEC（Reed-Solomon）编码

 

本文以IEEE 802.3 200/400GBASE-R使用的FEC RS(544,514)编码为载体，理解Reed-Solomon编码的数学过程。

有限域

Reed-Solomon编码的数学是定义在有限域（Finite Field）之上的，有限域的运算是可以硬件实现的，而且成本不很高。为保持文章篇幅，关于有限域的话题在文章（待补充）中单独讨论。

RS编码

RS编码会将需要编码的流数据重新排列为以「符号(symbol)」为单位的数据块，如下图：

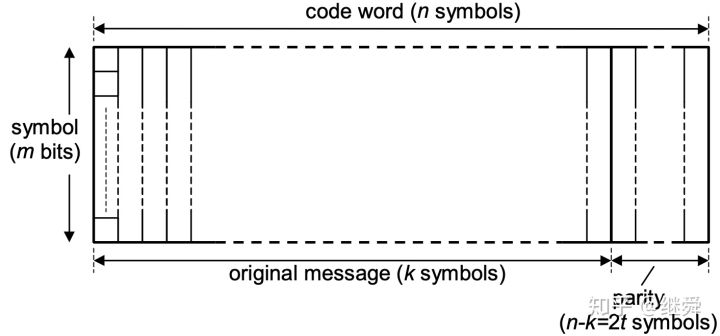
以200/400GBASE-R使用的RS(544,514)(注释：前面一个数字为生成编码长度，后面一个数字为原始信息数据长度)编码为例：

1. 每个Symbol数据10bits，(m=10)
2. 原始需要加密的数据是514个symbols，(k=514)
3. 校验数据为30个symbols，(2t=30)
4. 最终完成的编码为544个symbols，(n=544)

IEEE 802.3 119.2.4.6中定义了编码的算法：

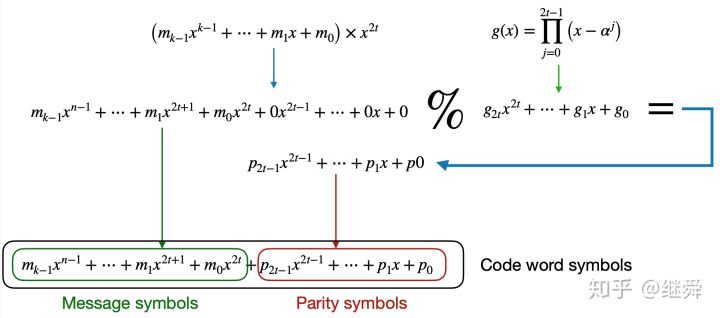
编码的数学过程并不复杂

1. 将原始需要编码的数据后面补30个0（上图「取余」运算符左侧部分，补0意思是为校验码占位）
2. 除以生成多项式  取余下的多项式为校验多项式 
3. 将校验多项式加到刚才补过0的编码数据多项式中，就是最终生成的编码

以一个简单点的例子来理解一下上面的计算过程：

1. 该编码为RS(15,11)
2. 原始数据为  （每个元素为一个symbol）
3. 后面补0后  并以多项式形式表示
4. 除以 
5. 取最终余数  加到补过0的原始数据中
6. 生成最终编码 
7. 注意以上运算均为有限域中的运算，primitive polynomial为 

以上就是Reed-Solomon编码的大致过程，相应的每种编码会有几种不同的硬件实现方案，这个以后再研究。

编码过程的本质是将k维的信息数据映射到了n维空间中，n维空间中的k维数据子空间与2t维校验空间是正交的。

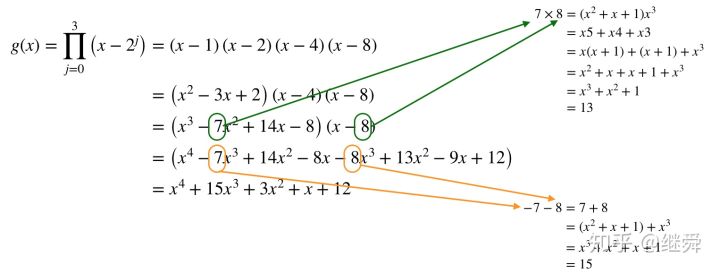
补充一点内容是关于生成多项式  的计算

 

以上面的简单例子中的生成多项式为例，计算过程如下：

IEEE标准中给出了RS(544,514)的运算参数，和运算完成后的多项式系数

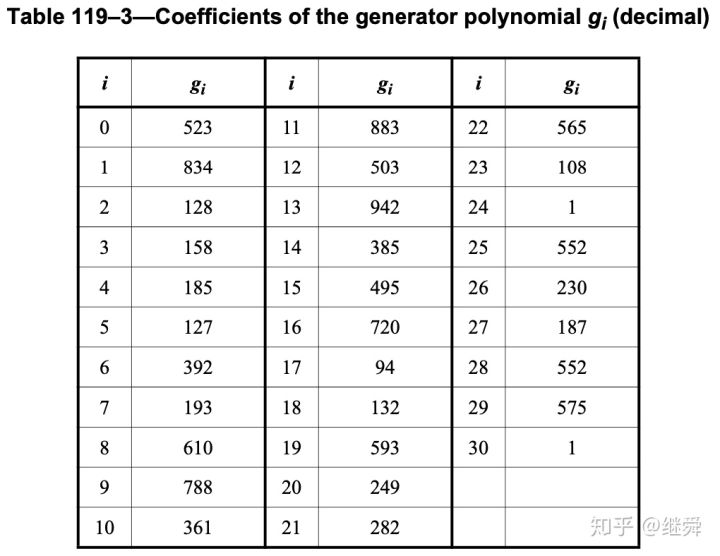
RS解码

由编码的生成过程可以知道，如果传输过程没有任何错误，那么接收到的编码数据块去除生成多项式  是可以整除、没有余数的。而再根据生成多项式的定义，就代表  是编码数据多项式的根，即 

如果传输过程中有错误，接收数据就是原始编码数据叠加上错误数据，这时再将  代入，结果将不是0，结果被称作「Syndrome」，而这个结果，只与引入的错误有关：

 

如果我们能获取错误出现的位置和值，就可以纠正错误。

假设有  个错误(  )，Syndrome就可以重写为：

 

我们先定位错误出现的位置，定义一个多项式(Error locator)

 

根据定义  是上面多项式的根，所以：

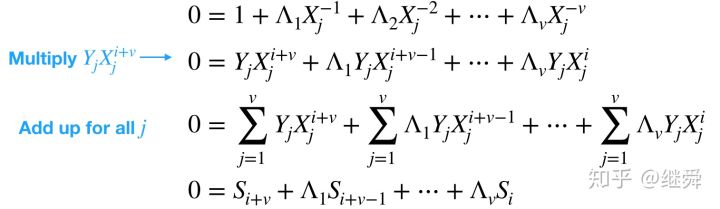
然后将根据接收数据计算出的Syndrome值，求解出系数  ，进而根据Error locator多项式定义（下式）求解出  ，从而获取到错误位置。

 

求出  后，再根据「Syndrome」公式求出  ，也就是错误的值

 

知道了错误的位置与值之后，就可以从接收数据中去掉错误，以恢复发送的编码数据了。

 

恢复编码数据之后，直接将校验数据丢掉，剩下的就是原始发送的信息数据。

我们仍然以前面的简单例子来看一下解码的计算过程（计算中使用的parity check matrix，用除  的方法是一样的效果）（接收数据注入了两个错误）

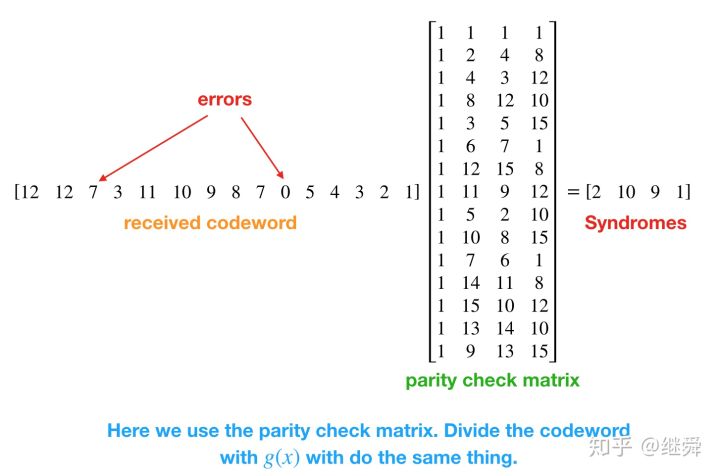
首先计算「Syndromes」值，结果为 

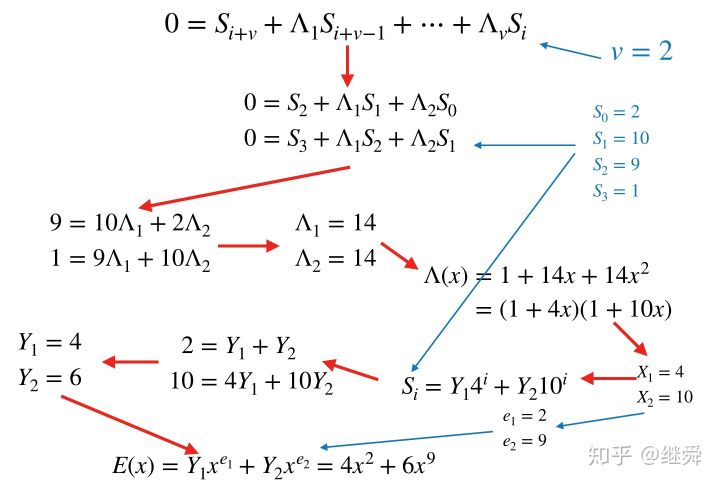
错误位置的定位为位置2和位置9，错误值为4和6（红色箭头为运算主线）

上图为最终纠错过程，可以看到错误被纠正。

对于RS(544,514)来说，运算过程会复杂的多，也有一些高效算法和硬件实现，不在本文的讨论范围。

总结

总结Reed-Solomon编解码的过程如下图

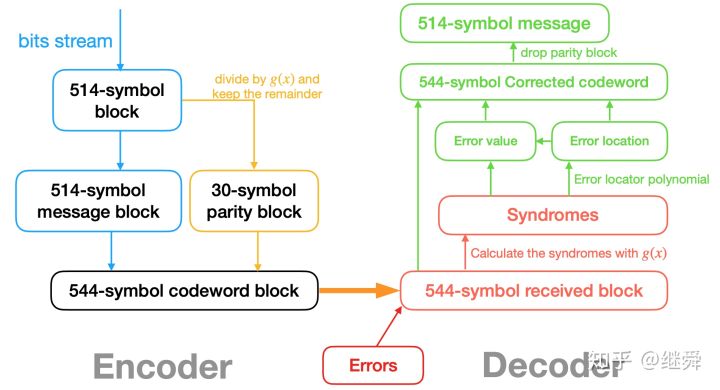
本文英文版slides文件见https://www.slideshare.net/ssuserc3f3de/understanding-reedsolomon-code

部分代码

有限域的模拟计算可以使用python的pyfinite库，但对于RS(544,514)来说需要修改一下默认的primitive polynomial系数

gPrimitivePolysCondensed = {
    1  : (1,0),
    2  : (2,1,0),
    3  : (3,1,0),
    4  : (4,1,0),
    5  : (5,2,0),
    6  : (6,4,3,1,0),
    7  : (7,1,0),
    8  : (8,4,3,2,0),
    9  : (9,4,0),
    #10 : (10,6,5,3,2,1,0),     #默认
    10 : (10,3,0),              #IEEE 802.3 RS(544,514)标准
……

以下代码为计算IEEE 802.3 RS(544,514)的生成多项式  系数的代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Tue Dec 31 03:03:25 2019

@author: wangjishun
calculate the coefficients of generating polynomial for RS(544,514) encoder
"""

from pyfinite import ffield1

# define parameters
m = 10
t2 = 30

F = ffield1.FField(m)
aj = []
atmp = 1
for j in range(t2):
    if j == 0:
        aj.append(atmp)
    else:
        atmp = F.Multiply(2,atmp)
        aj.append(atmp)

print('aj, (a0 first, a29 last)')
print(aj)
print('')
        
# calculate the coefficients
# g(x) = (x-1)(x-2)(x-2^2).....(x-2^29)
c = []
for aIdx, a in enumerate(aj):
    b = [1, a]
    if aIdx == 0:
        c = b
        continue
    coefs = []
    #print(b)
    #print(c)
    for i in range(len(b)+len(c)-1):
        bb = b[0:i+1]
        bc = bb[::-1]
        
        btmp = [0]*len(c)
        if i < len(b):
            for j in range(len(bc)):
                btmp[j] = bc[j]
        else:
            for j in range(len(bc)):
                btmp[j] = bc[j]
            s = i+1-len(bc)
            btmp = [0]*s + btmp[:-s]
        d = []
        for idx, e in enumerate(c):
            #dtmp = e*btmp[idx]
            dtmp = F.Multiply(e,btmp[idx])
            d.append(dtmp)
        dsum = 0
        for e in d:
            #dsum += e
            dsum = F.Add(dsum, e)
        #print(dsum)
        coefs.append(dsum)
    #print(coefs)
    c = coefs
#print(c)
print('g(x) coefficients gi, (g0 first, g30 last)')
print(c[::-1])

备注：

Parity check matrix的理解

参考资料：

• IEEE 802.3 119.2.4.6
• http://downloads.bbc.co.uk/rd/pubs/whp/whp-pdf-files/WHP031.pdf