卡罗需-库恩-塔克条件
在数学中,卡罗需-库恩-塔克条件(英文原名: Karush-Kuhn-Tucker Conditions常见别名: Kuhn-Tucker,KKT条件,Karush-Kuhn-Tucker最优化条件, Karush-Kuhn-Tucker条件,Kuhn-Tucker最优化条件,Kuhn-Tucker条件)是在满 足一些有规则的条件下,一个非线性规划(Nonlinear Programming)问题能有最优化解法的一个必要和充分条件。这是一个广义化拉格朗日乘数的成果。
考虑以下非线式最优化问题:
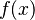 是需要最小化的函数,
是需要最小化的函数, 是不等式约束,
是不等式约束, 乃等式约束,
乃等式约束,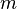 和
和 分别为不等式约束和等式约束的数量。
分别为不等式约束和等式约束的数量。
不等式约束问题的必要和充分条件初见于卡罗需(William Karush)的博士论文[1],之后在一份由W.卡(Harold W. Kuhn)及塔克(Albert W. Tucker)撰写的研讨生论文[2] 出现后受到重视。
目录[隐藏] |
[编辑]必要条件
假设有目标函数,即是要被最小化的函数 ,约束函数
,约束函数 及
及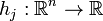 。再者,假设他们都是于
。再者,假设他们都是于 这点是连续可微的,如果
这点是连续可微的,如果 是一局部极小值,那么将会存在一组所谓乘子的常数
是一局部极小值,那么将会存在一组所谓乘子的常数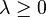 ,
,  及
及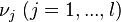 令到
令到
-
 。
。
[编辑]正则性条件或约束规范
于上述必要和充分条件中,dual multiplier 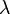 可能是零。当
可能是零。当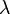 是零时,这个情况就是退化的或反常的。因此必要和充分条件会将约束的几何特性而不是将函数自身的特点纳入计算。
是零时,这个情况就是退化的或反常的。因此必要和充分条件会将约束的几何特性而不是将函数自身的特点纳入计算。
有一定数量的正则性条件能保证解法不是退化的(即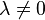 ),它们包括:
),它们包括:
- 线性独立约束规范(Linear independence constraint qualification)(LICQ):有效不等式约束的梯度(和等式约束的梯度于
 线性独立。
线性独立。
- Mangasarian-Fromowitz约束规范(Mangasarian-Fromowitz constraint qualification)(MFCQ):有效不等式约束的梯度和等式约束的梯度于
 正线性独立。
正线性独立。
- 常秩约束规范 (Constant rank constraint qualification) (CRCQ) :考虑每个有效不等式约束的梯度子集和等式约束的梯度,于
 的邻近区域的秩(rank)不变。
的邻近区域的秩(rank)不变。
- 常正线性依赖约束规范(Constant positive linear dependence constraint qualification)(CPLD):考虑每个有效不等式约束的梯度子集和等式约束的梯度,如果它们于
 是正线性依赖,那么它们于
是正线性依赖,那么它们于 的邻近区域也是正线性依赖。(如果存在
的邻近区域也是正线性依赖。(如果存在 not all zero令到
not all zero令到 ,那么
,那么 是正线性依赖)
是正线性依赖)
- 斯莱特条件(Slater condition):如果问题只包含不等式约束,那么有一点
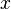 令到
令到 for all
for all 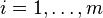
虽然MFCQ不等同于CRCQ,但可证出LICQ=>MFCQ=>CPLD,LICQ=>CRCQ=>CPLD。于实际情况下,较弱的约束规范会被倾向使用,这是因为较弱的约束规范能提供较强的最优化条件。
[编辑]充分条件
假设目标函数 及约束函数
及约束函数 皆为 凸函数,而
皆为 凸函数,而 是一仿射函数,假设有一可行点
是一仿射函数,假设有一可行点 ,如果有常数
,如果有常数 及
及 令到
令到
那么 这点是一全局极小值.
这点是一全局极小值.
[编辑]注释
- ^ W. Karush. Minima of Functions of Several Variables with Inequalities as Side Constraints, M.Sc. Dissertation. Dept. of Mathematics, Univ. of Chicago, Chicago, Illinois. 1939..此论文可于以下网址得到:http://wwwlib.umi.com/dxweb/details?doc_no=7371591 (需付费)
- ^ Kuhn, H. W.; Tucker, A. W.. Nonlinear programming. Proceedings of 2nd Berkeley Symposium. Berkeley: University of California Press. 1951: pp. 481-492.
[编辑]参考文献
- Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 0-486-43227-0.
- R. Andreani, J. M. Martínez, M. L. Schuverdt, On the relation between constant positive linear dependence condition and quasinormality constraint qualification. Journal of optimization theory and applications, vol. 125, no2, pp. 473-485 (2005).






























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








