三角剖分技术在图形领域,尤其是在三维重建领域是非常非常重要的技术,就拿我现在正在从事的3D打印行业来说吧,如果复杂曲面的三角剖分能够得以解决,那么我们这个行当绝大部分看似复杂的软件问题,都能轻易解决,因为对于提取点云,不管是硬件还是软件,成本是低廉的。要说三角剖分,首先要从Delaunay说起,它是目前三角剖分理论的基础,很多三维的剖分优化准则实际上是对它的扩展。
Delaunay三角网法则
Delaunay三角网为相互邻接而互不重叠的三角形的集合,每一个三角形的外接圆内不包含其他点,三角形的最小角最大。
按最小内角最大化原则形成的剖分也就是著名的Delaunay三角剖分(DT,DelaunayTriangulation),DT是许多领域实际应用中最受关注的一类,应用十分广泛,该剖分可追溯到G.Voronoi图,是于1907年提出的,后来Delaunay在1932年提出了解决该剖分完整而实用的方法,近几十年来该算法不断得到改进,以适应不同的应用.DT也就是最近点意义下的Voronoi(Dirichlet或Thiessen)图的直线对偶图,Voronoi图由许多胞元组成,每一个胞元包含点集中的一个点(每两点的垂直平分线将平面分成两部分,与某点对应的胞元实际是该点与点集中每个点垂直平分线在平面内所形成的交集),连接相邻胞元中两个点(直线段)便形成点集的DT.DT具有很多性质,剖分中常用的性质有最小内角最大和最大空圆原则.最小内角最大原则:对于一个凸四边形的两种剖分,DT获得的两个三角形中的最小内角最大.最大空圆原则:剖分中任一三角形的外接圆(三维为外接球面,高维为超球面)内不含有点集中的任何其他点.最小内角最大原则又称为局部最优准则,这样获得的剖分称为局部最优(或局部等角).关于DT的算法实现有很多,大致分为以下两大类,一类是增量算法,该法从点集的某一点开始,逐步进行,每一步增加一点,直至点集为空,常用的有Green—Sibson算法、Bowyer算法、Lawson算法、Cline—Renka算法等.另外,还有L—S算法、Watson算法、以及F—P算法等;另一类为分治算法,该法基于分而治之的思想,每次将点集分为规模相当的两个子集,分别进行递归实现,最后拼合,目前较好的有DeWall算法.二维三角剖分可以严格按照Delaunay三角网法则,目前这方面的理论已经非常成熟。
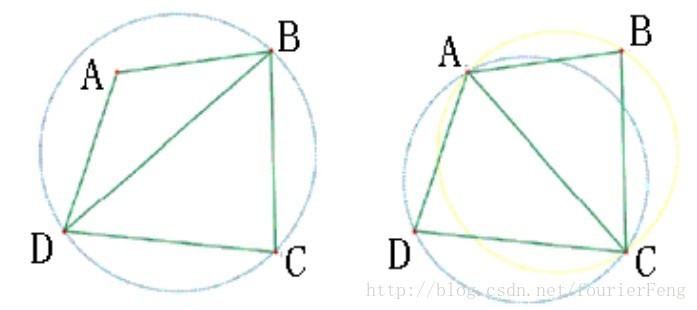
为了构造Delaunay三角网,Lawson提出的局部优化过程LOP(Local Optimization Procedure),一般三角网经过LOP处理,即可确保成为Delaunay三角网,其基本做法如下所示:
1.将两个具有共同边的三角形合成一个多边形。
2.以最大空圆准则作检查,看其第四个顶点是否在三角形的外接圆之内。
3.如果在,修正对角线即将对角线对调,即完成局部优化过程的处理。
LOP处理过程如下图所示:
一,L-S算 法
Lawson算法,即从任意的一个剖分开始,对出现的凸四边形施加最小内角最大原则进行对角线交换,直至完成.Lawson算法虽然能完全、正确地进行剖分,但计算量大,真正实现较为困难.Lee和Schachter继承了Lawson算法的边交换方法,具体实现作了改进,这种算法与Nelson算法相似,主要步骤如下:
(1)确定一个矩形区域,使所有的点位于该矩形内;
(2)将矩形分成大约n^1/2个箱(更小的矩形域);
(3)从一个箱开始记录点序,即对点重排序;
(4)置第一点于矩形中并连接此点与矩形的顶点,形成初始DT;
(5)加一新点于已有的DT中,必有一个三角形包围该点,连接新点与该三角形的顶点;
(6)若上一步形成凸四边形(最多4个),则依最小内角最大原则进行优化;
(7)每个点都被用过则转第8步,否则转第4步;
(8)最后删去所有与初始矩形顶点有一个公共顶点的三角形,余下的即为点集的三角剖分.与Lawson算法不同的是由于有前3步的预处理,搜索包围新点的三角形时的时间复杂度由原来的O(n)减少为O(n^1/2),总体复杂度大约为O(n)
这一算法的关键的第2步图示如下:
二,分而治之算法(由Shmaos和Hoey提出)
其基本思路是使问题简化,把点集划分到足够小,使其易于生成三角网,然后把子集中的三角网合并生成最终的三角网,用局部优化(LOP,即Local Optimiza—tion Procedure)算法保证其成为Delaunay三角网,它的优点是时间效率高,但需要大量递归运算,因此占用内存空间较多,如果计算机没有足够的内存,这一方法就无法使用;
三,三角网生长算法。
这类方法通常首先从点云数据中选定一个初始三角片(Seed Triangle),并作为网格曲面的种子面加入三角曲面集,三条边分别加入边界集。然后按照一定的规则从边界处向三角
曲面集中添加新的三角片元素,并实时刷新边界集,通过曲面网格由局部到整体的动态增长最终生成一张完整的三角网格曲面。
二维三角剖分技术已经非常成熟,而且网上现成的实现代码也很多;先说到这里,下面说一下三维曲面的三角剖分:
曲面剖分通常有两种方法,其一是将点投影到某一平面,运用平面的三角剖分算法完成剖分,而三维点问连接关系不变,这种方法将三维问题转化为平面问题,可称为平面投影法;其二是直接由三维点来构造剖分,称为直接剖分法.三角剖分通常有两种类型,第一类是三角剖分的顶点就是所给点集P,不改变原点集的拓扑结构,实质是对P的线性插
值;另外一类是在一定的误差范围内用剖分来逼近曲面,这时的顶点在数量和位置上均不同于原点集。
1,平面投影法
平面投影法就是将三维点投影到某平面,如x—y平面,然后对投影点集作平面域的三角剖分,最终形成的曲面三角剖分的点间连接关系与相应的投影点间的连接关系相同,这种方法的实质是平面域的三角剖分.近几年来在剖分研究方向、具体算法等方面有了很大的进展.当平面4点形成凸四边形时将有两种剖分,对采用哪一种三角剖分可以提出不同的选择原则,最常用的有最小内角最大化、边的总长度最小化即最小权等.
2,直接剖分算法
与平面投影法不同,直接剖分算法是直接根据三维散乱点构造三角剖分.实用的直接剖分算法很少,1988年Choi提出的一种增量算法[3是较好的一种方法,得到广泛的应用.Choi算法有下述几个重要概念:
(1)顶点、边、三角形、法矢散乱点集中的每一点在剖分中为三角形的顶点;3个顶点V1、V2、V3,如果满足det(V1、V2、V3)≠0 则这3点形成一个三角形;从原点看去,按逆 时针方向依次连接三角形顶点,相邻两点形成的有向边称为剖分的边;由上述有向边按右手准则来确定三角形的单位法矢.
(2)可见边
对于边AB,任一顶点P与它的关系有如下3种:
如果det(A,B,P)<0,则P.Right.AB;
如果det(A,B,P)=0,则P.On.AB;
如果det(A,B,P)>0,则P.Left.AB
若顶点(P.Right.AB),则称边AB相对点P可见,顶点A、B称为P的可见点.
(3)凸顶点、凸多边形
若一系列三维点形成的边封闭,三角形不相交,则这些点形成一个多边形.P、Q、R是按逆时针方向依次连接的3个点,若det(Q,R,P)>=0,则称Q是一个凸点;若det(Q,R,P)>0,则称Q为严格凸点.若多边形所有点都是严格凸点,则该多边形为严格凸多边形.
(4)轨迹生成
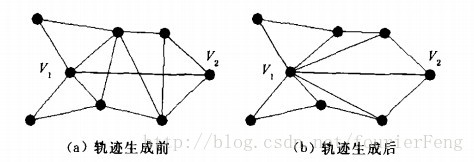
在工程应用中,曲面内部某些散乱点可能属于特定的轨迹线,如截面线、特征线等,为了准确地反映曲面形状,剖分中必须将这些点相互连接,以得到相应的轨迹线.
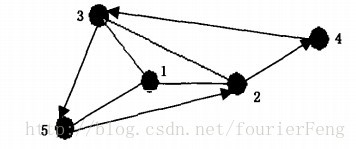
如下图所示,V1、V2为轨迹线上的点,按照轨迹生成算法,V1、V2必须连接,同时去掉与其相交的边.方法是首先判断、是否已经相连,若已相连则停止,否则搜索与相交的边e,对包含e的四边形交换对角线即去掉了边e.
(5)边界剪裁
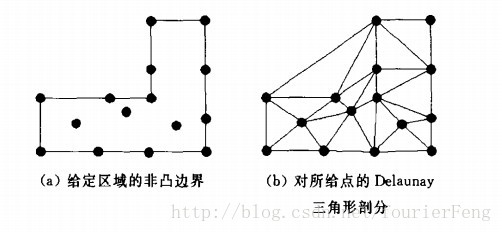
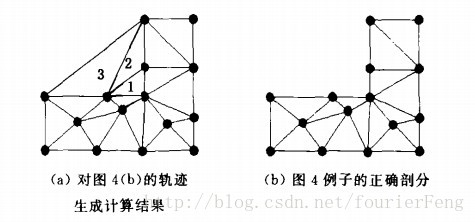
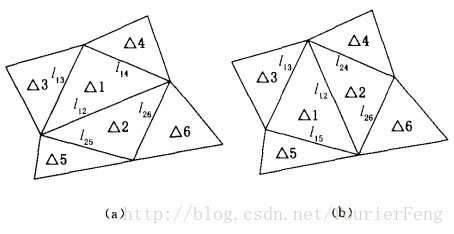
边界剪裁就是要从剖分中删去外边界环之外和内边界环之内“不合法”的三角形,对下图中的例子,
首先用轨迹生成算法获得满足要求的剖分,如下图中(a)所示,然后进行边界剪裁,去掉下图(a)中标号为1、2、3的3个三角形,最终获得正确的剖分如下图(b)所示.
Choi算法的简要步骤如下:
第1步预处理
①找到一个点Pc,使得从Pc点能够看到所有的散乱点,并作一过Pc的轴U;
②对所有的点做变换Pi—>Vi,Vi=Pi-Pc;
③按Vi与U的夹角大小,将Vi升序排列.
第2步三角剖分
①初始三角剖分
最初的剖分是从V1、V2开始,首先得到边V1V2,接着从V3开始逐点搜索,若共面则继续搜索,直至一不与前面点共面的顶点,连接此点与前面所有点从而构成初始剖分.如下图所示:
②剖分主过程
(a)下一个新N插入时,搜索N的所有可见点,并确定最左可见点LVN(V3)和最右可见点RVN(V4);
(b)构造一个三角形,它的顶点是N、LVN和LVN的下一点;
(c)若此时边界非凸,则继续从此非凸点开始与其下一点N构造三角形,并从TBL中删去该非凸点,直至边界为凸;
(d)处理完一个点,则将此点从点集中删除,若点集为空,则停止,否则转步骤(a).
第3步 轨迹生成.
第4步 边界剪裁.
Choi算法实际上仅仅是二维三角剖分的一种扩展,它要求以点云中的一点为原点的极坐标系,所有点对角度变量为一一映射,这样就极大的限制了它的使用范围。
曲面剖分优化准则
优化准则的选取直接影响到剖分结果.当剖分的两个三角形形成一个凸四边形时,存在两种剖分形式,这时须依据一定的准则来确定.曲面剖分常用的优化准则有外接曲面拟圆准则、标量积最大、空间形状优化准则以及光顺准则等,其中外接曲面拟圆准则是单侧性准则和模拟圆准则的广义形式,它和标量积最大准则只单纯考虑形成凸四边形的两个三角形之间的关系,而空间形状优化准则以及光顺准则则考虑两个三角形周围的4个三角形对剖分的影响.
1,外接曲面拟圆准则
外接曲面拟圆准则是二维剖分中的外接圆准则(Delaunay)和三维的外接球准则在曲面剖分中的推广形式,也是单侧性准则和模拟圆准则的广义形式.
单侧性准则称:曲面剖分的三角形的一侧不含有点集中的任一点,则称该三角形为局部最优;
模拟圆准则称:若三角形的一侧没有满足如下条件的点:在点集中且向三角形平面的投影落在该三角形的外接圆内,则称该三角形为局部最优.
由于这两个准则与外接圆准则(Delaunay)和三维的外接球准则不能统一描述,且在避免病态三角形方面尚有不足,因此资料1提出了外接曲面拟圆准则.
外接曲面拟圆:给定曲面 E上不共线的3 点P1、P2 、P3 , 它们确定的平面的单位法矢为n,以三角形△P1P2P3的外接圆圆心为起点沿n方向可以确定一射线,该射线与E的交点为C ( 若有多个交点则取最远处的点) ,以C 为中心,以C P1为半径的球与E的交称为△P1P2P3关于 E的外接曲面拟圆.
外接曲面拟圆准则:曲面上3 点组成三角形,若外接曲面拟圆区域内没有内环且不含有点集中任意点,则称该三角形局部最优 .
资料1同时还证明了以下两个结论:
( 1 ) 满足外接曲面拟圆准则必满足模拟圆准则;
( 2 ) 外接曲面拟圆准则等价于单侧性准则.
2,标量积最大准则
标量积最大准则是指对剖分形成的凸四边形,存在的两种剖分,计算每一剖分两个三角形单位法矢的标量积,取最大的一个剖分.标量积最大也就是形成剖分的两个三角形平面夹角最大,更趋于平坦.
3,空间形状优化准则
空间形状优化准则是指剖分形成的两个三角形有5条棱边,根据周围4个相邻的三角形判断各棱边的凹凸性,凸者边值为1,凹者边值为一1,共面时边值为0,计算两种情形下的5条边边值之和的绝对值K,取K值大的一种为最优剖分.具体下图所示,图中lij表示三角形i与三角形j的公共棱边的凹凸,公共棱边为凸时,其边值为1;公共棱边为凹时,其值为一1;两个三角形共面时,其值为0.接着分别计算K
Ka=abs(zl2+z25+z26+z14+z13)
Kb=abs(zl2+z25+z26+zl4+zl3)
比较它们的大小,取K 值较大的那种剖分
线性插值的保凸性和光顺性会直接影响插值曲面保凸和光顺的程度,空间形状优化准则的出发点就是由剖分生成各类连续曲面时,生成的曲面比较光顺.
4,光顺准则
光顺准则是Choi算法中采用的剖分准则,剖分中两个三角形形成的凸四边形的每条边为两个三角形所共有,分别计算这两个三角形单位法矢标量积,这样对应每一种剖分就有4个标量积值,计算4个标量积的最小值,取最小值最大的一种剖分作为最优剖分.
另外,三维剖分的难点还有对边界的处理,包括边界闭合的情况。
目前有几篇论文是针对这类课题的,主要描述如下:
先需要几个基本概念:
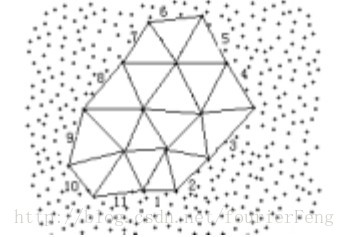
定义1. 边界边.在三角划分过程中,位于已划分区域和未划分区域之间的三角形边称为边界边(如下图所示,边1~11为边界边).
定义2. 边界环.在三角划分过程中,由边界边按逆时针或顺时针方向依次首尾相连构成的环称为边界环(如下图所示,边1~11按逆时针方向构成边界环).
定义3. 最优顶点.设点P为未划分区域离散点集中的任意一点,若点P与某边界边AB构成的三角形最接
近正三角形,则称点P为边界边AB的最优顶点.
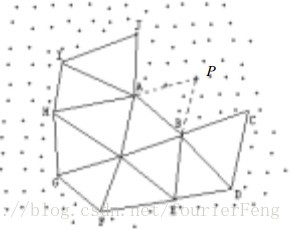
定义4. 可见顶点.设点P为未划分区域对应测量点集中的任意一点,且点P为某边界边AB的最优顶点.若点P与另一边界边BC构成的三角形不与已划分区域折叠,并且最大内角不超过θ,则称点P为边界边BC的可见顶点.如下图所示,点P为边AJ和边BC的可见顶点,而不是边CD,DE,EF等的可见顶点.
下面则是针对边界问题的重点:
边界环的裂变与融合
在3D 空间对离散数据进行三角划分的基本思想是:由初始三角形开始,从已划分区域边界向未划分区域逐步扩展形成新的三角形,直至三角网格覆盖整张曲面.三角网格在3D 空间随着离散数据点的分布而扩展,不需要将数据点向二维平面投影,复杂曲面也不需要分片投影.在算法实现的过程中,发现三角网格并不是简单地扩展,还会出现已划分区域隔离和相遇的情况.因此,在基本算法的基础上,又提出了边界环裂变和边界环融合的新概念,以使算法能够适应各种形态的曲面.下面我们通过对非封闭曲面、封闭曲面和多连通封闭曲面划分情况的分析来引出这两个概念
1,非封闭曲面
从非封闭曲面的离散点集中取出3个点,构成初始三角形,此时的边界边为初始三角形的三条边.由初始三角形开始,为每一条边界边寻找最优顶点,向未划分区域扩展生成新的三角形,直到已划分区域覆盖整张曲面.由于曲面是非封闭的,在三角网格向未划分区域扩展的过程中,一个已划分区域与另一个已划分区域不会相遇.
2,简单封闭曲面
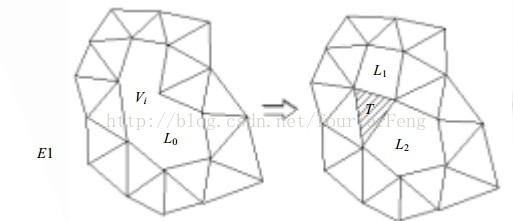
封闭曲面由于没有边界,在三角网格向未划分区域扩展的过程中,会出现已划分区域相遇的情形,需要将相遇的已划分区域缝合起来,使得三角网格也是封闭的.如下图所示,三角划分最终形成边界环L0.
(1) 若 L0 的边界边数( 记为bedge_num)>4,则为边界环L0 中的每一条边界边寻找最优顶点.当为边界环L0 中的一条边界边E1寻找最优顶点时,首先遍历L0中的每一个结点V1…Vn,发现有结点Vi 与边界边E1能构成较优三角形,则连接Vi与E1的两端点,构成三角形T.此时三角形T将边界环L0分裂成两个边界环L1和L2,再对边界环L1和L2分别处理.若L0中未发现有任何结点能与边界边E1构成较优三角形,则在未划分区域的离散数据点中为边界边E1寻找最优顶点.这种因为三角网格缝合而产生的一个边界环分裂成两个边界环的过程就称为边界环的裂变;
(2) 若L0的bedge_num=4(如图3中的边界环L1),则连接四边形的对角线生成两个三角形,边界环封闭;
(3) 若L0的bedge_num=3,就由此3条边界边构成一个三角形,边界环封闭.所有的边界环最终都会收缩为bedge_num=4或bedge_num=3的情形.当所有的边界环处理完毕时,封闭曲面的三角划分结束,从而得到一张封闭的三角网格.
3,多连通封闭曲面
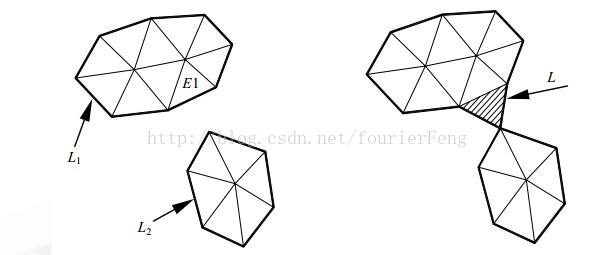
与简单封闭的曲面三角化过程一样,在三角网格向未划分区域扩展的过程中,多连通封闭曲面(如图6中的零件表面)的边界环也会发生裂变,且由于多连通封闭曲面的法矢变化复杂,在三角划分过程中还会发生两个边界环融合形成一个边界环的情况,如图4所示.在三角划分过程中,有两个边界环L1,L2.当为边界环L1中的某一条边界边E1寻找最优顶点时,遍历L2中的每一个结点V1…Vn,发现有结点Vi 与边界边E1能构成较优三角形,则连接Vi 与E1的两端点,构成三角形T.此时三角形T将边界环L1,L2连接成一个边界环L,再对边界环L进行处理,继续向未划分区域扩展.这种因为三角网格缝合而产生的两个边界环合并成一个边界环的过程称为边界环的融合.
以上蓝字部分皆引用自参考资料2,文中的算法或许仅仅对边界有用,对稍微复杂点的曲面以及不太均匀的点云分布则是无能为力的!
绿字皆引用自参考资料3,资料3分析现有的研究成果非常细腻,是很好的参考文献。
但是目前为止,复杂的三维三角剖分还是一个未解决的问题,也就是说,目前的已有算法只能针对相对规则的图形(接近严格凸集),以及点云均匀分布的情况。
我尝试用函数拟合去处理点云分布不太均匀的情况,剖分出来的模型可以在形状上趋近于真实图形,可是会发生大量的三角面片相交的情况。见下图(远处的为点云,近处的是用线性函数拟合剖分的结果):
主要是因为严格的三角抛分是需要回溯的(类似于动态规划),也就是经常需要对已经抛分的面片重新调整 ,针对三维的这个回溯过程我暂时还没有实现,希望能有老师为我指点迷津。
已经有不少文献提出将点云进行分层,然后再三维重建来间接的进行三角剖分。 针对这样的思路我将做一些工作,希望能有比较好的结果吧。
参考资料:
1,孔德慧,陈其明,汪叔淳.一种新的曲面剖分优化准则 [ J ] .工程图学学报,1995 ,16 (1):28 ~34 .
2,肖双九,邱泽阳,张树生,杨海成.多连通曲面离散点集的3D三角划分算法研究 .软件学报,2002,13(4).
3,张永春 ,达飞鹏, 宋文忠.三维散乱点集的曲面三角剖分.中国图象图形学报,2013年12月






















 1780
1780











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








