圆心坐标的提取

用OpenCV的话，这样的活儿也就那么两三行代码，而且灵活可靠。但是，玩图像处理只懂玩成这样就悲哀了，就如同游戏引擎之于计算机图形学，太依赖图像库是不利于自己的成长和知识的提升的。

       圆心提取的本质是从一张含有圆形/椭圆标志物的图片（见下图1，现实图片经各种处理到达这种圆与背景分明的样态）中，选择一定坐标系，提取出各个标志圆的圆心在这个坐标系中的坐标。

       因此这个坐标系的选择将是影响最终结果的形式的关键。一般来说选择图像坐标系，以像素为单位。本实验图片的格式是BMP，因此可以按照BMP自身的坐标特点，以图片左下角为坐标原点，向右为X轴，向上为Y轴。当然若想与WINDOWS窗口坐标系一致（以左上角为原点），直接用图片高度减上坐标系的结果就行了。

       关于结果的精度是很值得考究的事情。事实上，若考虑到素材图片是相机所拍成像的，某个圆的圆心与坐标原点的距离应该是一个含一定精度的浮点实数。但是计算机图像的结构限定了坐标系只能以像素为单位，因此其可能达到的最高精度只有0. 5像素。在此以上的精度在本素材图像中是没有意义的。因为相机会自动对物理场景（连续）的采样点（离散采样）进行向输出图像的一一映射，形成像素（一个像素只包含一款颜色）。相邻像素的值是非连续（离散）的，注定图像坐标系中每个“值”（坐标）都只能与像素相容。这样，圆心位置也就只能存在于某个像素上或某2个或4个像素之间，因此实际中最高只有0.5的精度。

 

 
（图1  圆心提取素材图片）

图2 数字图像本质——被离散化采样，导致精度最高仅0.5）

但是，如果圆心不是通过直接寻找的，而是采用数值计算得到（譬如本实验中用到的径向误差判断结合法），那么计算结果就会存在比较高的精度的可能性。这是理论可得结果与实际可得结果的差别。但就“计算机图像”这层意义来说，高于0.5的精度意义不大。

算法的设计：

在分析之后对算法的设计和选择就清晰了——立足于图像的本质上的话，只需要把圆心所在的像素位置找到，或者把包围圆心位置的几个像素找到即可。

参见图2，可知，图像中的参照物为一个圆或椭圆。在把它看作理想的圆/椭圆的话，可以认为圆点必然是在X方向横跨最多像素点的那一行中。因此算法设计上，针对每个圆，首先找出满足这个条件的一行（或几行，取中间行或中间两行），然后在Y方向上找到该像素行的中间位置，即为圆心——综合来说，圆心位置可能是落在某一个像素上，或X方向两个像素之间，或Y方向两个像素之间，或XY方向的4个像素之间。算法必须考虑这几种情况，算出精度为0.5的圆心位置。

算法的实现重点在于怎样分离出一个一个的圆，我采用的是逐像素法，先处理完最开头的一个圆（底部坐标靠近左下角原点），然后把这个圆从图像中去除（对二值化图像，就是把该圆的白色像素变黑），之后再处理下一个圆（寻得条件同样是，底部坐标靠近左下角原点）……直到处理完。怎么判断处理完呢？具体就是当该图像完全黑化的时候停止继续寻觅圆。

圆心坐标用一个容器链表保存起来，作为输出——输出到文件或作为一个/几个白像素涂入被完全黑化的图像上。

该算法为自主设计，自称为逐像素处理。应用条件是：
（1） 图片为二值化黑白图片，8BIT。（可以通过简单的预处理达到）
（2） 图片中仅含圆形。（本实验素材满足，若不满足可进行一定的预处理，如形态学处理，空间模板处理）

上方法另外作出的一个假设：该圆为理想的圆/椭圆。但是从图2这个放大图来说，事实上并不理想——虽然也可满足以上算法能找到圆心。把该圆规范化成一个标准的圆，这样可使找出的圆心具有更高的可信度。

按照某文献资料(图像处理中圆心算法研究 - 雷家勇,达飞鹏,孟广猛，东南大学自动化研究所)中所叙述的方法，可采用“径向误差预处理的最小二乘”进行拟合计算。

算法可分为三部分：
1. 找出初始圆心（此圆心作为径向误差判断的基准，在本实验中可直接取用逐像素处理法所得的结果）。
2. 找出拟合用的像素坐标。首先这些像素必须是圆形的边缘单像素（即八邻域内最多3个像素）；然后进行筛选，这主要通过径向误差范围判断，去除无效的边界点和误差大的边界点。
3. 根据上述处理后的边界点，用最小二乘法拟合圆心。

因为经历了数值计算，因此结果将具有高精度，但不一定有意义（见4.1）。本方法结合了“逐像素法找初始圆心”——“径向误差筛选出拟合数据”——“最小二乘法拟合、修正圆心”，得到可信度更高的圆心方位。

该算法（径向误差最小二乘法）的适用条件为：
（1） 处理的图像元素必须是严格的圆或近似圆。如果是椭圆且偏心太厉害的话，全部基于圆的拟合算法会不适用，径向误差方法也变得无效。
（2） 因为采用了逐像素处理，因此也必须满足之前所述该算法的条件。

有此设计的处理结果是:

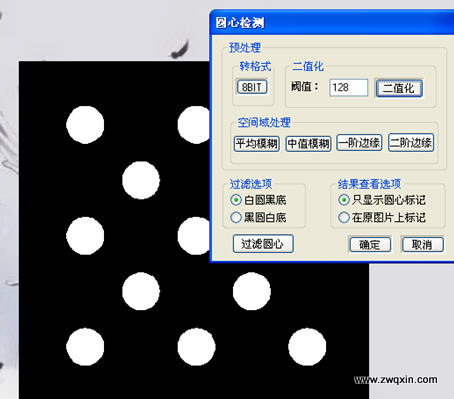
（图3  程序界面，圆心提取对话框）

（图4  结果）

(图5  直观一点)

（图6  另一张测试图片）

（图7  处理结果）

最后这里只是说明对于这种杂乱排布的圆也能检测出而已。不过扫描算法里的递归终结条件就得好好掂量了~

程序内嵌进LVideoCapture .ver 1.5里了。（1.0版的功能见[VFW视频捕获之尝试] ）在后面的1.8版本，涉及了摄象机标定的功能。