【深度优先搜索DFS】

【DFS】

推荐视频链接
推荐好文

核心思想：一条路走到黑，不撞南墙不回头

运用手段：栈

简述：(推荐好文中有详述)

简单的说，就是对于一个点，我先确定四个方向，当他每次朝我规定的方向走到一个能走的点时，我便先仅仅关注走完后的这个点，再继续走，继续换关注对象。当我关注的这个点走到不能再走的时候，就要返回到上一个点。继续走下一个方向，以此类推，直到找到答案

例题：

1.遍历

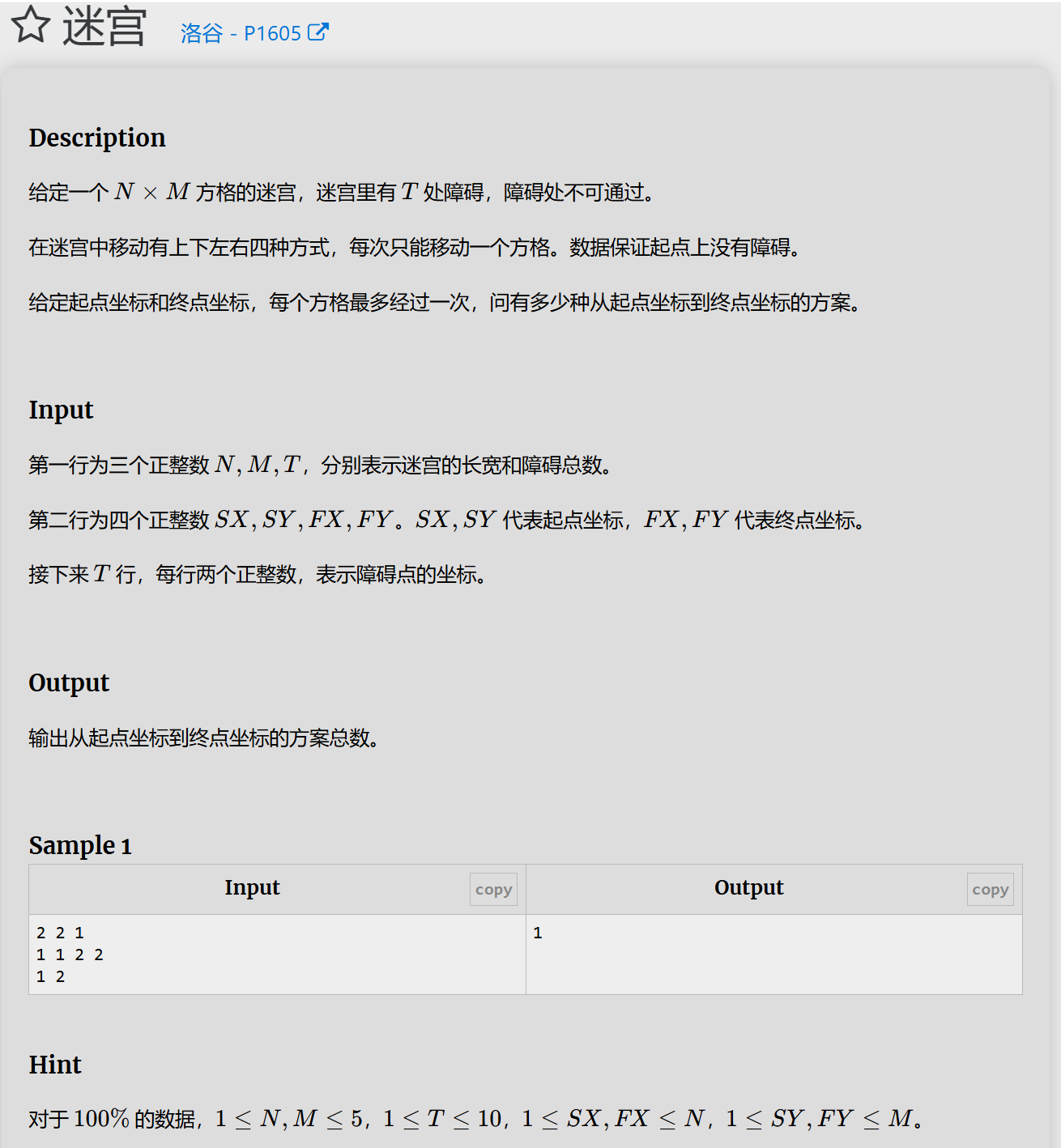
代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;

bool G[10][10],s[10][10];//G表地图，s表判定数组(判定是否已经走过了) 
int d[]={-1,0,1,0,-1};//方向数组 
int sx,sy,fx,fy;//起点/终点 
int cns;//答案 
int n,m,t;

void dfs(int x,int y)
{
	if(x==fx && y==fy)//当到了终点时，答案加一，退回去继续找 
	{
		cns++;
		return;
	}
	
	for(int i=1;i<=4;i++)//四个方向 
	{
		int l=x+d[i],r=y+d[i-1];//方向 
		if(l>=1&&r>=1&&l<=n&&r<=m&&!G[l][r]&&!s[l][r])//不能到地图外去,不能是障碍,不能重复走 
		{
			s[l][r]=1;//先标记，跟特设起点一个意思 
			dfs(l,r);//关注下一个点 
			s[l][r]=0;//我已经走完了，回去再走的时候就不能说我走过这了 
		}
	}
}


signed main()
{
	
	cin>>n>>m>>t;
	cin>>sx>>sy>>fx>>fy;
	G[sx][sy]=1;//特设起点为障碍，因为每个点只能走一次，如果无特设可能会先上走又下走回到起点再继续往终点走，错误
	while(t--)
	{
		int ax,ay;
		cin>>ax>>ay;
		G[ax][ay]=1; 
	}
	dfs(sx,sy);
	cout<<cns;
	
	return 0;
 } 

2.连通块

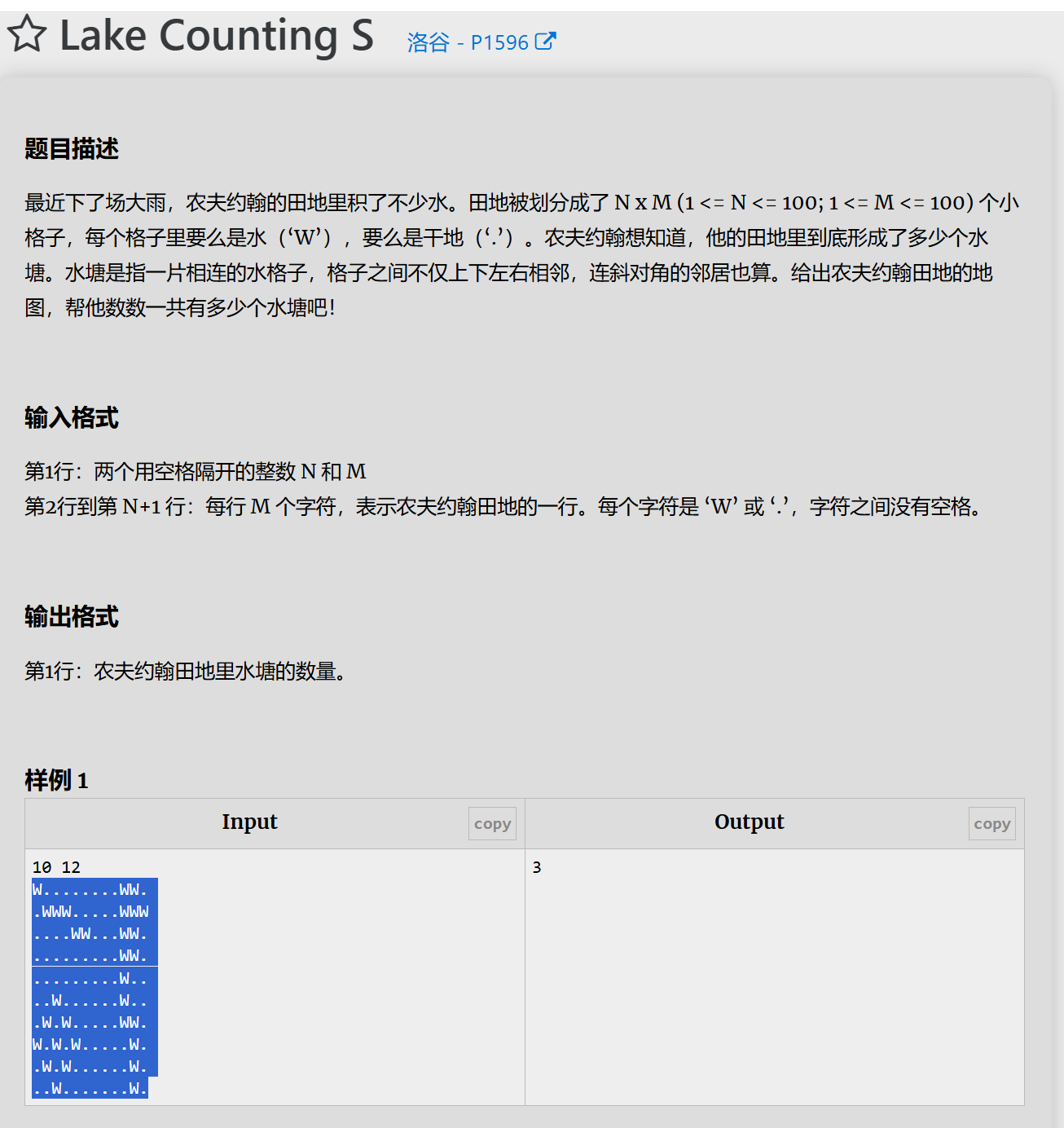
#include <bits/stdc++.h>
#define int long long
using namespace std;

char g[110][110];//地图 
bool s[110][110];//判断数组 
int n,m;
int cns;//答案 
int dx[]={1,1,1,-1,-1,-1,0,0};//方向数组 
int dy[]={1,0,-1,1,0,-1,1,-1};


void dfs(int x,int y)
{
	for(int i=0;i<=7;i++)//8个方向 
	{
		int sx=x+dx[i],sy=y+dy[i];
		if(sx>=1&&sx<=n&&sy>=1&&sy<=m&&g[sx][sy]=='W'&&!s[sx][sy])//不能走出地图外,需要是连着的W,并且还不能被标记过 
		{
			s[sx][sy]=1;//没被标记过,现在标记 
			dfs(sx,sy);//继续找下一个 
		}
	}
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			cin>>g[i][j];
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(g[i][j]=='W' && !s[i][j])//如果他是W,并且没有被标记,就说明找到了新的池塘 
			{
				cns++;//找到了新的池塘 
				s[i][j]=1;//标记他，说明找过了 
				dfs(i,j);
			}
		}
	}
	cout<<cns<<endl;
	
	return 0;
}