分支限界求解TSP问题

TSP问题中,任意一条完整路径上的每个城市都有两条边,一条进入城市,一条离开城市.

所以对于任意一个路径的费用矩阵而言,每一行(列)中的最小值(不包括由A到A的点对角线上的).

是必须要用到的费用.

 

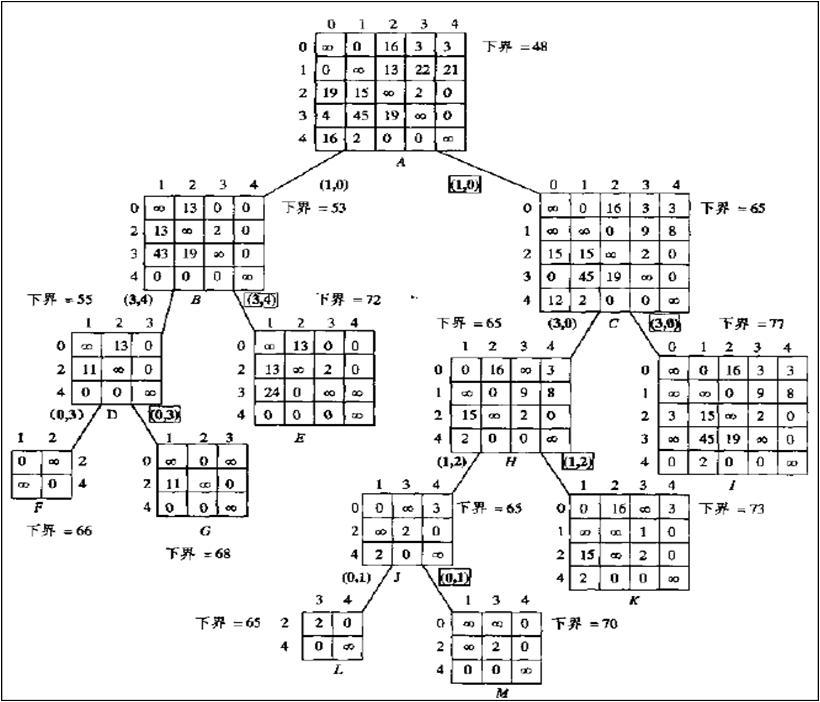
左支的生成可直接去掉所展开的0元素所在的行和列(依据引理选取要展开的结点:

选取要展开的矩阵.矩阵的选取是选取当前下界值最小的矩阵.
展开结点的选取.每个归约后的矩阵将会有至少n(n为该节点的矩阵维数)个0元素.选取哪个来展开?
  由于任何一个结点的展开都是分为两支,左支为选择了当前元素(城市),右支则是在当前位置不选该元素.
  对于待选择的0元素而言,如果将其展开,其右支的归约值较大,则说明选择该点为最优路径的可能性较高.因为最优路径的值是固定的,如果选取的展开元素比其它的0元素的右支的值更大,则其左支就相对更小的概率就会更大.

注:当然这个只是有更大的概率而并不是说肯定是最优路径上的点.

 

左支的生成可直接去掉所展开的0元素所在的行和列(依据引理1并对已生成路径(一条/多条)进行避免回路操作,防止再次选中该城市,这里采用将回路元素设置为+∞将来实现.右支则直接将该元素设置为+∞,防止发生二次展开.
对生成的两个结点进行归约操作,并更新归约值h,将结点放入结点表中,选择当前归约值最小的矩阵作为要展开的结点,再选择0元素,然后继续生成左支和右支.
当所选矩阵为二维矩阵的时候,直接连接两个0元素所在城市即可获得最优的路径.