由遍历序列还原二叉树结构

当给出一棵二叉树，我们可以知道它的先序、中序和后序遍历。那么我们是否能够根据先序、中序或者后序的遍历序列来还原出这棵二叉树呢？

首先通过二叉树的一种遍历序列是无法还原二叉树的。如果在二叉树的三种遍历序列中给出其中的两种，是否可以唯一确定一棵二叉树呢？

• 由二叉树的先序和中序遍历序列可以唯一确定一棵二叉树。因为，二叉树的先序遍历必先访问根结点D，其次遍历左子树L，然后遍历右子树R。即在先序遍历序列中，第一个结点必为根结点；而在中序遍历中，先遍历左子树L，然后访问根结点D，最后遍历右子树R，因此中序遍历序列被根分为两部分：根结点之前的部分为左子树结点中序序列，根结点之后的为右子树结点中序序列。通过这两部分再到先序序列中找到左右子树的根结点，以此类推，便可唯一得到一颗二叉树。

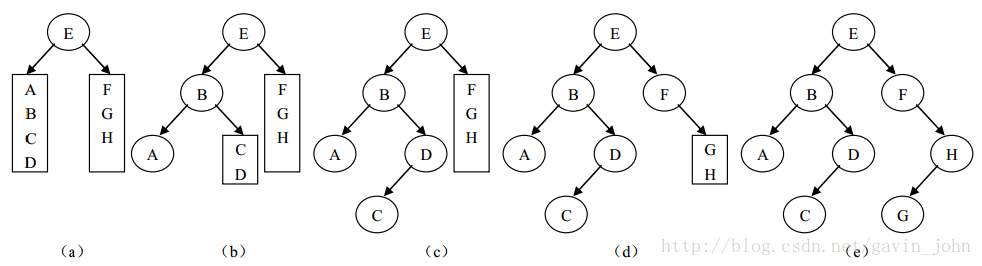
例如：已知一颗二叉树的先序序列为EBADCFHG，其中序序列为ABCDEFGH。下图说明了还原二叉树的过程：

首先由先序序列知道二叉树的根结点为E，则其左子树的中序序列为ABCD，右子树的中序序列为FGH。反过来知道二叉树的先序序列为BADC，右子树先序序列为FHG。然后二叉树的左右子树分别用先序和中序序列分析其根结点及其左右子树，知道得到整个二叉树结构。

• 同样的，由二叉树的后序和中序遍历序列也可以唯一确定一棵二叉树。还原的方法与上述类似，只不过此时根结点是出现在后序序列的最后面。

• 由先序和后序序列不能唯一确定一棵二叉树。例如，先序序列为AB，后序序列为BA，此时就无法确定二叉树的结构，因为B既可以是A的左子树，也可以是根A的右子树。