《编译原理》实验二-递归下降语法分析器的构建-实验报告

一、实验要求

  运用递归下降法，针对给定的上下文无关文法，给出实验方案。预估实验中可能出现的问题。

二、实验方案

1、构造LL(1)分析表
  分析给定文法，消除左递归及提取左因子，以使文法符合LL(1)文法。计算First集合、Follow集合，并根据First集合和Follow集合构造LL(1)分析表。
2. 输入输出设计
  严格来说，输入的字符串首先通过词法分析得到Token序列，再经过本算法得到分析树。但是本次实验的输入较为简单，且侧重点在于后者，故仅对输入串进行简单的判断，生成Token序列。输入字符串中的单个字符表示一个Token。一个字母即是一个identifier，一个数字即为一个number。
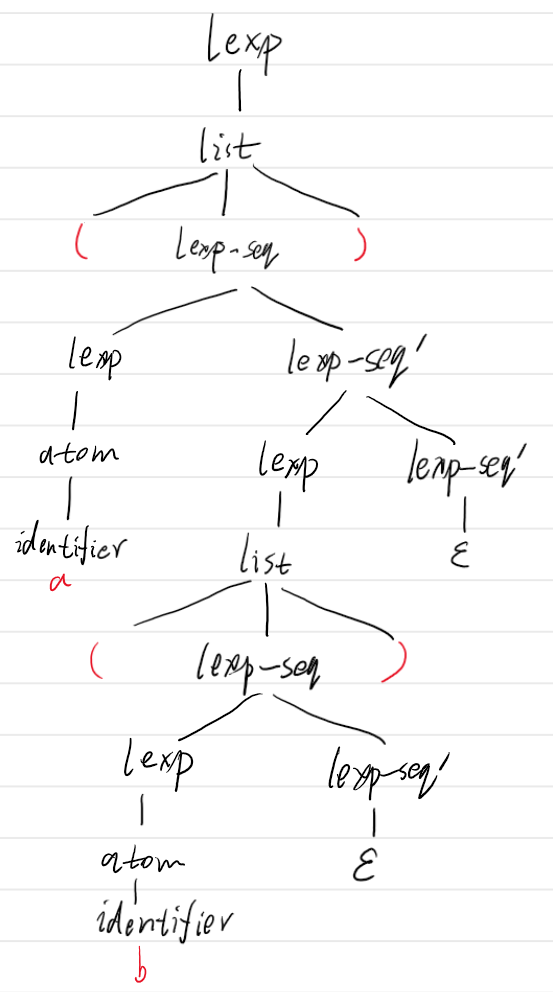
  输出形式为解析得到的语法分析树。以缩进形式表示树的父子关系。例如，对于下左图所示的分析树，输出形式为下右图所示。

  若解析失败，输出失败提示，并将分析树输出，以显示发生错误的结点位置，如下图：

3. 数据结构设计
  程序使用树来存储得到的分析树，由于该分析树是一般的树状结构，采取树的孩子兄弟表示法。从而用二叉树的存储结构来表示树的逻辑结构。结点设计如下：

struct TreeNode
{
   
	string flag = "";
	Token* token = NULL;
	TreeNode* firstChild = NULL;
	TreeNode* nextSibling = NULL;
};

  其中Token为算法输入的数据结构，设计如下：

struct Token
{
   
	MyTokenType tokenType;
	string value;
};

三、预估问题

1、预估问题

给定文法可能不是LL(1)文法，或无法构造出LL(1)分析表。

2、理论基础

• First集合的定义
    令X为一个文法符号或ε，则集合First(X)的定义如下：
    1.若X是终结符或ε，则First(X) = {X}。
    2.若X是非终结符，则对于每个产生式 X→X₁X₂…X_n，First(X)都包含了First(X₁) - {ε}。若对于某个i<n，所有的集合First(X₁), …, First(X_i)都包括了ε, 则First(X)也包括了First(X_i+1) - {ε}。若所有集合First(X₁), …, First(X_n)包括了ε，则First(X)也包括ε。
• Follow集合的定义
    集合Follow(A)的定义如下：
    1.若A是开始符号，则$就在Follow(A)中。
    2.若存在产生式B→αAγ，则First(γ) - {ε}在Follow(A)中。
    3.若存在产生式B→αAγ，且ε在First(γ)中，则Follow(A)包括Follow(B)。
• LL(1)文法的定义
    定义：如果文法G相关的LL(1)分析表的每个项目中至多只有一个产生式，则该文法就LL(1)文法。
    定理：若满足以下条件，则BNF中的文法就是LL(1)文法：
    1.在每个产生式A→α₁|α₂|…|α_n中，对于所有的i和j：1≤i，j≤n，i≠j，First(α_i)∩First(α_j)为空。
    2.对于每个非终结符A,若First(A)包含了ε，那么First(A)∩Follow(A)为空。
• LL(1)分析表的构造方法
    LL(1)分析表M[N, T]的构造：为每个非终结符A和产生式A→α重复以下两个步骤：
    1.对于First(α)中的每个记号a，都将A→α添加到项目M[A, a]中。
    2.若ε在First(α)中，则对于Follow(A)的每个元素a（记号或是$），都将A→α添加到M[A, a]中。

四、内容和步骤

1、针对4.8习题输入和输出的设计及代码

• 习题4.8文法：

    lexp→atom|list
    atom →number|identifier
    list→(lexp-seq)
    lexp-seq→lexp-seq lexp|lexp
  

• 消除左递归

    lexp→atom|list
    atom →number|identifier
    list→(lexp-seq)
    lexp-seq→lexp lexp-seq’
    lexp-seq’→lexp lexp-seq’|ε
  

• 计算First集合

    First(lexp) = { number, identifier, ( }
    First(atom) = { number, identifier }
    First(list) = { ( }
    First(lexp-seq) = { number, identifier, ( }
    First(lexp-seq’) = { number, identifier, ( ,ε}
  

• 计算Follow集合

    Follow(lexp) = { $, number, identifier, (, ) }
    Follow(atom) = { $, number, identifier, (, ) }
    Follow(list) = { $, number, identifier, (, ) }
    Follow(lexp-seq) = { ) }
    Follow(lexp-seq’) = { ) }
  

• 构造LL(1)分析表

M[N,T]	number	identifier	(	)	$
lexp	lexp→atom	lexp→atom	lexp→list
atom	atom→number	atom→identifier
list			list→(lexp-seq)
lexp-seq	lexp-seq→lexp lexp-seq’	lexp-seq→lexp lexp-seq’	lexp-seq→lexp lexp-seq’
lexp-seq’	lexp-seq’→lexp lexp-seq’	lexp-seq’→lexp lexp-seq’	lexp-seq’→lexp lexp-seq’	lexp-seq’→ε

• 输入(a(b(2))(c))，得到分析树
  

2、针对现场给定语法的设计和处理

• 给定文法：

    E→E+T|T
    E→T*F|F
    F→(E)|id
  

• 提取左因子

    E→TE’
    E’→+TE’|ε
    T→FT’
    T’→*FT’|ε
    F→(E)|id
  

• 计算First集合

    First(E) = { (, id }
    First(E’) = { +,ε}
    First(T’) = { (, id }
    First(T’) = { *,ε}
    First(F) = { (, id }
  

• 计算Follow集合

    Follow(E) = { $, ) }
    Follow(E’) = { $, ) }
    Follow(T) = { +, $, ) }
    Follow(T’) = { +, $, ) }
    Follow(F) = { *, +, $, ) }
  

• 构造LL(1)分析表

M[N,T]	id	(	)	+	*	$
E	E→TE’	E→TE’
E’			E’→ε	E’→+TE’		E’→ε
T	T→FT’	T→FT’
T’			T’→ε	T’→ε	T’→*FT’	T’→ε
F	F→id	F→(E)

• 输入(a+b)*c，得到分析树
  

3、实验具体步骤

①分析文法，消除左递归并提取左因子，使文法符合LL(1)文法
②计算First集合及Follow集合
③构造LL(1)分析表
④根据LL(1)分析表设计代码
⑤运行与调试

五、实验结果

1、代码

• 针对习题4.8代码

#include <iostream>
#include <iomanip>
#include <string>
#include <windows.h>

using namespace std;

string typeName[6] = {
    "undefine","number","identifier","leftBracket","rightBracket","endInput" };
enum MyTokenType
{
   
	undefine, number, identifier, leftBracket, rightBracket, endInput
};

struct Token
{
   
	MyTokenType tokenType;
	string value;
};

//采用孩子兄弟表示法的树节点
struct TreeNode
{
   
	string flag = "";
	Token* token = NULL;
	TreeNode* firstChild = NULL;
	TreeNode* nextSibling = NULL;
};

void input();
TreeNode* lexp();
TreeNode* atom();
TreeNode* list();
TreeNode* lexp_seq();
TreeNode* lexp_seq1();

TreeNode* match();
TreeNode* errorNode();

void printTree(TreeNode* head, int depth = 0, bool isFirst = false);

Token inputToken[1024];
int tokenNumber = 0;
int curPos = 0;
bool error = false;

int main() {
   
	input();
	curPos = 0;
	while (inputToken[curPos].tokenType != endInput && !error)
	{
   
		TreeNode* head = lexp();
		if(error)
			cout << "解析token失败，发生错误的结点如下所示：" << endl;
		printTree(head);
	}
	
	return 0;
}

//可将输入按实验一识别为Token字符串，但这里仅做简单判断(一个字符为一个Token)
void input() {
   
	cout << "请输入：";
	char ch;
	while ((ch = getchar()) != '\n') {
   
		inputToken[tokenNumber].value = ch;
		if (ch == '(')
			inputToken[tokenNumber].tokenType = leftBracket;