7个案例讲透时间复杂度：从O(N²)到O(logN)的算法效率跃迁指南-CSDN博客

7个案例讲透时间复杂度：从O(N²)到O(logN)的算法效率跃迁指南

【免费下载链接】LeetCode-Book 《剑指 Offer》 Python, Java, C++ 解题代码，LeetBook《图解算法数据结构》配套代码仓项目地址: https://gitcode.com/GitHub_Trending/le/LeetCode-Book

你是否曾遇到这样的困境：明明正确的代码却在大数据测试时超时？LeetCode提交时因"时间限制 exceeded"反复碰壁？本文将通过7个实战案例，从理论到实践帮你彻底掌握时间复杂度分析，让你的算法效率实现质的飞跃。读完本文你将获得：识别低效算法的火眼金睛、复杂度优化的实用技巧、10+高频题目的复杂度分析模板。

一、时间复杂度基础：算法效率的度量衡

时间复杂度（Time Complexity）是衡量算法执行时间随输入数据量增长的变化趋势，它反映了算法的计算操作数量与输入规模N的关系。与实际运行时间不同，时间复杂度忽略了编程语言、硬件性能等环境因素，只关注核心的增长规律。

1.1 为什么要关注时间复杂度？

当N=1000时，O(N²)算法需要执行10⁶次操作，而O(N log N)仅需约10⁴次（相差100倍）。在LeetCode的大数据测试用例中，这种差距直接决定了代码能否通过。以LCR 170. 交易逆序对的总数为例，暴力解法（O(N²)）在N=50000时需要2.5×10⁹次操作，而归并排序优化后（O(N log N)）仅需50000×16≈8×10⁵次，差距达3000倍。

1.2 常见复杂度等级与增长曲线

从优到劣排序，常见时间复杂度包括：

O(1) < O(log N) < O(N) < O(N log N) < O(N²) < O(2ⁿ) < O(N!)

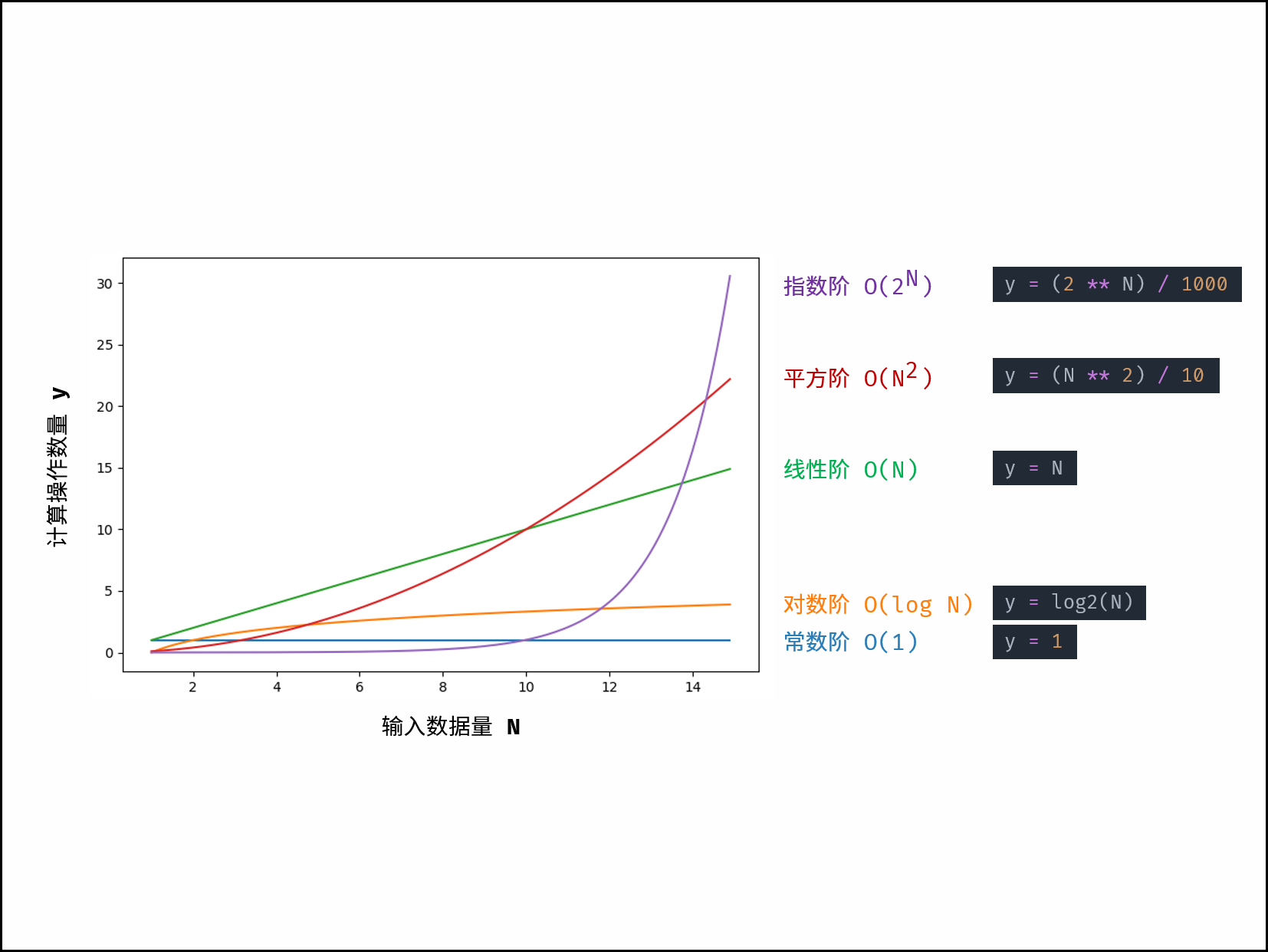
时间复杂度增长曲线

其中：

常数阶O(1)：操作次数固定，如LCR 133. 位 1 的个数的位运算解法
对数阶O(log N)：每次操作将问题规模减半，如二分查找
线性阶O(N)：操作次数与N成正比，如LCR 126. 斐波那契数的迭代解法
线性对数阶O(N log N)：主流高效排序算法的复杂度，如归并排序、快速排序
平方阶O(N²)：双层嵌套循环的典型复杂度，如冒泡排序

详细理论可参考官方文档：# 1.3 时间复杂度.md

二、实战分析：从代码识别时间复杂度

2.1 O(1)常数阶：与输入规模无关的操作

特征：无循环或递归，操作次数固定。

def count_one_bits(n):
    count = 0
    while n:
        n &= n - 1  # 清除最低位的1
        count += 1
    return count  # 无论n多大，循环次数不超过32（整数位数）

典型应用：剑指 Offer 15. 二进制中 1 的个数，无论输入n多大，循环次数最多为整数的位数（如32位/64位），因此复杂度为O(1)。

2.2 O(log N)对数阶：二分思想的高效体现

特征：问题规模按固定比例（通常是1/2）减少。

def my_pow(x, n):
    if n < 0:
        x = 1 / x
        n = -n
    res = 1
    while n > 0:
        if n % 2 == 1:
            res *= x
        x *= x  # 底数平方
        n = n // 2  # 指数减半
    return res

这是LCR 134. Pow(x, n).md)的快速幂解法，每次循环将n减半，因此循环次数为log₂n，时间复杂度O(log N)。当n=10²⁴时，仅需约80次循环（2⁸⁰≈10²⁴）。

2.3 O(N)线性阶：一次遍历解决问题

特征：单层循环或递归，操作次数与N成正比。

def training_plan(courses):
    slow = fast = 0
    while fast < len(courses):
        if courses[fast] != 0:
            courses[slow] = courses[fast]
            slow += 1
        fast += 1
    return courses[:slow]

这是LCR 141. 训练计划 III的双指针解法，每个元素仅被访问一次，时间复杂度O(N)。线性阶是算法设计的基础目标，大多数数组、链表的遍历操作都应控制在O(N)级别。

三、复杂度优化实战：从O(N²)到O(N log N)的蜕变

3.1 案例1：逆序对统计的暴力与优化

问题：统计数组中的逆序对数量（剑指 Offer 51. 数组中的逆序对）

暴力解法（O(N²)）：

def reverse_pairs(nums):
    count = 0
    for i in range(len(nums)):
        for j in range(i+1, len(nums)):
            if nums[i] > nums[j]:
                count += 1
    return count  # N=50000时超时

归并排序优化（O(N log N)）：在归并排序的合并阶段，当右子数组元素小于左子数组元素时，左子数组剩余元素均与当前右元素构成逆序对。

def reverse_pairs(nums):
    def merge_sort(l, r):
        if l >= r: return 0
        m = (l + r) // 2
        res = merge_sort(l, m) + merge_sort(m+1, r)
        i, j = l, m+1
        tmp[l:r+1] = nums[l:r+1]
        for k in range(l, r+1):
            if i == m+1:
                nums[k] = tmp[j]
                j += 1
            elif j == r+1 or tmp[i] <= tmp[j]:
                nums[k] = tmp[i]
                i += 1
            else:
                nums[k] = tmp[j]
                j += 1
                res += m - i + 1  # 统计逆序对
        return res
    
    tmp = [0] * len(nums)
    return merge_sort(0, len(nums)-1)

归并排序将问题分解为两个子问题（各O(N log N/2)），合并阶段O(N)，总复杂度T(N) = 2T(N/2) + O(N) = O(N log N)。

3.2 案例2：滑动窗口最大值的优化之路

问题：239. 滑动窗口最大值，在O(N)时间内解决

暴力解法（O(Nk)，k为窗口大小）：

def max_sliding_window(nums, k):
    return [max(nums[i:i+k]) for i in range(len(nums)-k+1)]

单调队列优化（O(N)）：维护一个存储索引的单调队列，保证队首始终是窗口最大值。

from collections import deque

def max_sliding_window(nums, k):
    q = deque()  # 存储索引，对应元素单调递减
    res = []
    for i, num in enumerate(nums):
        # 移除窗口外的元素
        while q and q[0] <= i - k:
            q.popleft()
        # 维护队列单调性
        while q and nums[q[-1]] < num:
            q.pop()
        q.append(i)
        # 窗口形成后开始记录结果
        if i >= k - 1:
            res.append(nums[q[0]])
    return res

每个元素仅入队出队一次，总操作次数O(N)，实现了线性时间复杂度。

四、复杂度陷阱：那些容易被忽略的细节

4.1 隐藏的O(N²)：循环条件的迷惑性

def trap(height):
    res = 0
    for i in range(len(height)):
        left_max = max(height[:i+1])  # O(i)操作
        right_max = max(height[i:])   # O(N-i)操作
        res += min(left_max, right_max) - height[i]
    return res

这是接雨水问题的暴力解法，表面看是单层循环，但每次循环中的max操作实际是O(N)，因此总复杂度O(N²)。正确优化应使用双指针将其降至O(N)。

4.2 递归的复杂度计算：树的深度决定一切

斐波那契数列的递归实现：

def fib(n):
    if n <= 1: return n
    return fib(n-1) + fib(n-2)

递归树呈指数增长，时间复杂度O(2ⁿ)。优化方案包括：

迭代法（O(N)时间，O(1)空间）
矩阵快速幂（O(log N)时间）
公式法（O(1)时间）

五、实战总结：复杂度优化工具箱

5.1 常用优化策略

复杂度类型	优化方向	典型算法	应用场景
O(N²) → O(N log N)	分治法	归并排序、快速排序	逆序对统计
O(N²) → O(N)	双指针	两数之和、三数之和	LCR 179. 查找总价格为目标值的两个商品
O(Nk) → O(N)	单调队列/栈	滑动窗口、柱状图面积	239. 滑动窗口最大值
O(2ⁿ) → O(N)	动态规划	斐波那契数列、背包问题	LCR 126. 斐波那契数
O(N) → O(log N)	二分查找	搜索旋转数组、平方根计算	LCR 172. 统计目标成绩的出现次数

5.2 复杂度分析三步法

拆解操作：将算法分解为基本操作（循环、递归、函数调用）
确定规模：找到影响复杂度的输入规模N（数组长度、树节点数等）
计算次数：分析基本操作的执行次数与N的数学关系

六、进阶资源与实战练习

6.1 推荐学习资料

官方复杂度教程：# 1.2 算法复杂度.md
排序算法复杂度对比：# 7.1 排序算法简介.md
动态规划复杂度分析：# 11.1 动态规划解题框架.md

6.2 复杂度优化训练清单

LCR 128. 库存管理 I：O(N²)→O(N)
剑指 Offer 49. 丑数：O(N log N)→O(N)
LCR 161. 连续天数的最高销售额：O(N²)→O(N)
剑指 Offer 53 - I. 在排序数组中查找数字 I：O(N)→O(log N)

掌握时间复杂度分析不是一蹴而就的，需要在实际解题中不断练习。建议每次写完代码后，主动分析其时间复杂度，并思考是否有优化空间。当你能一眼看出O(N²)算法的优化点时，就真正入门了算法设计的精髓。收藏本文，下次遇到超时问题时回来对照，相信你的算法效率会有显著提升！

创作声明：本文部分内容由AI辅助生成（AIGC），仅供参考