简单易学的机器学习算法——Latent Dirichlet Allocation（理论篇）

最新推荐文章于 2024-04-15 14:28:09 发布

zhiyong_will

最新推荐文章于 2024-04-15 14:28:09 发布

阅读量2.2w

点赞数 12

分类专栏：机器学习，数据挖掘算法深度学习Deep Learning 文章标签： LDA 概率主题模型机器学习

本文链接：https://blog.csdn.net/google19890102/article/details/50504870

版权

深度学习Deep Learning 同时被 2 个专栏收录

79 篇文章 114 订阅

订阅专栏

机器学习，数据挖掘算法

60 篇文章 493 订阅

订阅专栏

引言

LDA(Latent Dirichlet Allocation)称为潜在狄利克雷分布，是文本语义分析中比较重要的一个模型，同时，LDA模型中使用到了贝叶斯思维的一些知识，这些知识是统计机器学习的基础。为了能够对LDA原理有清晰的认识，也为了能够对贝叶斯思维有全面的了解，在这里对基本知识以及LDA的相关知识进行阐述，本系列包括两个部分：

Latent Dirichlet Allocation——理论篇
Latent Dirichlet Allocation——实践篇

在理论篇中将重点阐述贝叶斯相关的知识和LDA的基本思想，基本的知识点包括Gamma函数和分布，Beta函数和分布，Dirichlet函数和分布，贝叶斯定理，Gibbs采样等等。在接下来的文章，我们通过以下几个方面具体介绍LDA的核心思想：

基础知识：二项分布，多项式分布，Gamma分布，Beta分布，Dirichlet分布，贝叶斯定理，共轭分布
文本建模：Unigram Model，概率主题模型，Gibbs采样以及贝叶斯推理

一、基础知识

在贝叶斯思维以及LDA中需要使用到一些概率的知识，下面我们罗列下会使用到的一些基本知识。

1、二项分布

二项分布是概率分布里面最简单也是最基本的分布，要理解二项分布，我们首先得定义 $n$ 次独立重复试验的概念： $n$ 次独立重复试验是指在相同的条件下，重复做的 $n$ 次试验称为 $n$ 次独立重复试验。

假设对于一个事件 $A$ ，在一次试验中，其发生的概率为 $p$ ，那么其不发生的概率为 $1-p$ ，那么在 $n$ 次独立重复试验中事件 $A$ 恰好发生 $k$ 次的概率为：

P n (k) = C k n p k (1 - p) n - k

$P_n\left ( k \right )=C_n^kp^{k}\left ( 1-p \right )^{n-k}$

在这里，参数 $k$ 是一个随机变量，便称这样的随机变量 $k$ 服从二项分布，记为： $k\sim B\left ( n,p \right )$ 。

可以验证下式成立：

\sum k = 0 n P n (k) = \sum k = 0 n C k n p k (1 - p) n - k = 1

$\sum _{k=0}^{n}P_n\left ( k \right )=\sum _{k=0}^{n}C_n^kp^{k}\left ( 1-p \right )^{n-k}=1$

2、多项式分布

多项式分布是二项分布的一个推广形式，在二项分布中，事件 $A$ 的取值可能只能是发生或者是没有发生，而在多项式分布中事件 $A$ 的取值可能有 $k$ 种，取每一种可能的概率为 $p_i$ ，其中 $p_i$ 满足：

\sum i = 1 k p i = 1

$\sum _{i=1}^{k}p_i=1$

多项式分布的概率形式为：

P (x 1, x 2, \dots, x k; n; p 1, p 2, \dots, p k) = n ! x 1 ! x 2 ! \dots x k ! p x 1 1 p x 2 2 \dots p x k k

$P\left ( x_1,x_2,\cdots ,x_k\; ;n\; ;p_1,p_2,\cdots ,p_k \right )=\frac{n!}{x_1!x_2!\cdots x_k!}p_1^{x_1}p_2^{x_2}\cdots p_k^{x_k}$

3、Gamma分布

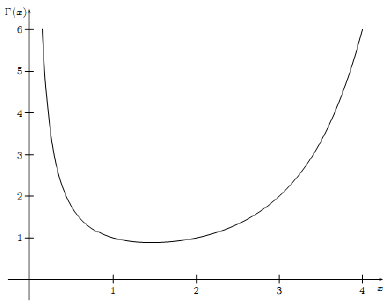
Gamma函数的具体形式如下：

Γ (x) = \int \infty 0 e - u u x - 1 d u

$\Gamma \left ( x \right )=\int_{0}^{\infty }e^{-u}u^{x-1}du$

其中， $x> 0$ 。Gamma函数的图像如下所示：

这里写图片描述

Gamma函数 $\Gamma \left ( x \right )$ 具有如下的一些性质：

性质1：

Γ (x + 1) = x Γ (x)

$\Gamma \left ( x+1 \right )=x\Gamma \left ( x \right )$

这个性质可以通过分部积分的方法得到证明，证明如下：

Γ (x + 1) = \int \infty 0 e - u u x d u = \int \infty 0 - u x d e - u = - u x e - u ∣ \infty 0 - \int \infty 0 - e u x u x - 1 d u = x \int \infty 0 e - u u x - 1 d u = x Γ (x)

$\begin{matrix} \Gamma \left ( x+1 \right )=\int_{0}^{\infty }e^{-u}u^{x}du\\ =\int_{0}^{\infty }-u^{x}de^{-u}=-u^xe^{-u}\mid _0^{\infty }-\int_{0}^{\infty }-e^{u}xu^{x-1}du\\ =x\int_{0}^{\infty }e^{-u}u^{x-1}du=x\Gamma \left ( x \right ) \end{matrix}$

性质2：

Γ (1) = 1, Γ (1 2) = π \sqrt

$\Gamma \left ( 1 \right )=1,\; \Gamma \left ( \frac{1}{2} \right )=\sqrt{\pi }$

性质3：

Γ (n + 1) = n!

$\Gamma \left ( n+1 \right )=n!$

4、Beta分布

Beta函数的具体形式如下：

B e t a (a, b) = \int 10 x a - 1 (1 - x) b - 1 d x

$Beta\left ( a,b \right )=\int_{0}^{1}x^{a-1}\left ( 1-x \right )^{b-1}dx$

其中， $a> 0,\; b>0$ 。Beta函数有如下的一个性质：

B e t a (a, b) = Γ ( a ) Γ ( b ) Γ ( a + b )

$Beta\left ( a,b \right )=\frac{\Gamma \left ( a \right )\Gamma \left ( b \right )}{\Gamma \left ( a+b \right )}$

上述的关于Beta函数的性质将Beta函数与Gamma函数联系起来，对于该性质的证明如下所示：

Γ (a) Γ (b) = \int \infty 0 e - u u a - 1 d u \cdot \int \infty 0 e - v v b - 1 d v = \int \infty 0 \int \infty 0 e - (u + v) u a - 1 v b - 1 d u d v

$\begin{matrix} \Gamma \left ( a \right )\Gamma \left ( b \right )=\int_{0}^{\infty }e^{-u}u^{a-1}du\cdot \int_{0}^{\infty }e^{-v}v^{b-1}dv\\ =\int_{0}^{\infty }\int_{0}^{\infty }e^{-\left ( u+v \right )}u^{a-1}v^{b-1}dudv\\ \end{matrix}$

此时，令 $z=u+v$ ， $t=\frac{u}{u+v}$ ，上式可转化为：

Γ (a) Γ (b) = \int \infty 0 \int 10 e - z (z t) a - 1 [z (1 - t)] b - 1 z d z d t = \int \infty 0 e - z z a - 1 z d z \cdot \int 10 t a - 1 (1 - t) b - 1 d t = Γ (a + b) \cdot \int 10 t a - 1 (1 - t) b - 1 d t = Γ (a + b) \cdot B e t a (a, b)

$\begin{matrix} \Gamma \left ( a \right )\Gamma \left ( b \right )=\int_{0}^{\infty }\int_{0}^{1}e^{-z}\left ( zt \right )^{a-1}\left [ z\left ( 1-t \right ) \right ]^{b-1}zdzdt\\ =\int_{0}^{\infty }e^{-z}z^{a-1}zdz\cdot \int_{0}^{1}t^{a-1}\left ( 1-t \right )^{b-1}dt\\ =\Gamma \left ( a+b \right )\cdot \int_{0}^{1}t^{a-1}\left ( 1-t \right )^{b-1}dt\\ =\Gamma \left ( a+b \right )\cdot Beta\left ( a,b \right ) \end{matrix}$

由此可知： $Beta\left ( a,b \right )=\frac{\Gamma \left ( a \right )\Gamma \left ( b \right )}{\Gamma \left ( a+b \right )}$ 。

5、Dirichlet分布

Dirichlet函数的基本形式为：

D (a 1, a 2, \dots, a k) = \int \dots \int x a 1 - 1 1 \dots x a k - 1 k d x 1 \dots d x k

$D\left ( a_1,a_2,\cdots ,a_k \right )=\int \cdots \int x_1^{a_1-1}\cdots x_k^{a_k-1}dx_1\cdots dx_k$

其中， $x_1\cdots x_k\geqslant 0$ ， $\sum _{i=1}^{k}x_i=1$ 。而Dirichlet分布的概率密度函数为：

p (x 1, \dots, x k) = 1 D ( a 1 , \dots , a k ) x a 1 1 \dots x a k k

$p\left ( x_1,\cdots ,x_k \right )=\frac{1}{D\left ( a_1,\cdots ,a_k \right )}x_1^{a_1}\cdots x_k^{a_k}$

其中， $0\leqslant x_1\cdots x_n\leqslant 1$ ，且 $\sum_{i=1}^{k}x_k=1$ ， $D\left ( a_1,\cdots ,a_k \right )$ 的形式为：

D (a 1, \dots, a k) = Γ ( a 1 ) \dots Γ ( a k ) Γ ( a 1 + \dots + a k )

$D\left ( a_1,\cdots ,a_k \right )=\frac{\Gamma \left ( a_1 \right )\cdots \Gamma \left ( a_k \right )}{\Gamma \left ( a_1+\cdots +a_k \right )}$

注意到Beta分布是特殊的Dirichlet分布，即 $k=2$ 时的Dirichlet分布。

6、贝叶斯定理

贝叶斯定理中牵涉到概率的一些基本知识，包括：

条件概率
联合概率
边缘概率

条件概率的表达形式为： $P\left ( A\mid B \right )$ ，其表示的含义是事件 $A$ 在事件 $B$ 发生的条件下发生的概率。

联合概率的表达形式为： $P\left ( A,\; B \right )$ ，其表示的含义是事件 $A$ 和事件 $B$ 同时发生的概率。

事件 $A$ 的边缘概率的表达形式为： $P\left ( A \right )$ ，其表示的含义是事件 $A$ 发生的概率。

有了以上的定义，贝叶斯定理可以通过如下的贝叶斯公式表示：

P (B ∣ A) = P ( A ∣ B ) P ( B ) P ( A )

$P\left ( B\mid A \right )=\frac{P\left ( A\mid B \right )P\left ( B \right )}{P\left ( A \right )}$

对于上述的贝叶斯公式， $P\left ( B \right )$ 称为先验概率，即在得到新的数据前某一假设的概率； $P\left ( B\mid A \right )$ 称为后验概率，即在得到了新的数据后，对原假设的修正； $P\left ( A \right )$ 称为标准化常量； $P\left ( A\mid B \right )$ 称为似然度。

对于两个相互独立的事件的联合概率有如下的性质：

P (A, B) = P (A) P (B)

$P\left ( A,\; B \right )=P\left ( A \right )P\left ( B \right )$

7、共轭分布

有了如上的贝叶斯定理，对于贝叶斯派而言，有如下的思考方式：

先验分布+样本信息 $\Rightarrow$ 后验分布

上述的形式定义是贝叶斯派的思维方式，人们对于事物都会存在着最初的认识（先验分布），随着收集到越来越多的样本信息，新观察到的样本信息会不断修正人们对事物的最初的认识，最终得到对事物较为正确的认识（后验分布）。若这样的后验概率 $P\left ( \theta \mid x \right )$ 和先验概率 $P\left ( x \right )$ 满足同样的分布，那么先验分布和后验分布被称为共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

有了如上的的共轭先验分布的定义，有如下的两个性质：

1、Beta分布是二项分布的共轭先验分布，即：

$B e t a (p ∣ α, β) + C o u n t (m 1, m 2) = B e t a (p ∣ α + m 1, β + m 2)$ $Beta\left ( p\mid \alpha ,\beta \right )+Count\left ( m_1,m_2 \right )=Beta\left ( p\mid \alpha +m_1 ,\beta +m_2 \right )$

对于上式，对于事件 $A$ ，假设其发生的概率为 $p$ ，不发生的概率为 $1-p$ ，发生的次数为 $m_1$ ，不发生的概率为 $m_2$ ，且有 $m_1+m_2=n$ 。则对于参数 $m_1$ ，则有：

P (m 1 ∣ p) = p m 1 (1 - p) n - m 1 = p m 1 (1 - p) m 2

$P\left ( m_1\mid p \right )=p^{m_1}\left ( 1-p \right )^{n-m_1}=p^{m_1}\left ( 1-p \right )^{m_2}$

而对于参数 $p$ ，则是服从参数为 $\alpha$ 和 $\beta$ 的Beta分布：

P (p ∣ α, β) = p a - 1 ( 1 - p ) b - 1 \int 1 0 p a - 1 ( 1 - p ) b - 1 d p

$P\left ( p\mid \alpha ,\beta \right )=\frac{p^{a-1}\left ( 1-p \right )^{b-1}}{\int_{0}^{1}p^{a-1}\left ( 1-p \right )^{b-1}dp}$

已知在贝叶斯定理中有如下的公式成立：

P (B ∣ A) = P ( A ∣ B ) P ( B ) P ( A ) \propto P (A ∣ B) P (B)

$P\left ( B\mid A \right )=\frac{P\left ( A\mid B \right )P\left ( B \right )}{P\left ( A \right )}\propto P\left ( A\mid B \right )P\left ( B \right )$

则对于上述的后验概率，即为：

P (p ∣ m 1) = P ( m 1 ∣ p ) \cdot P ( p ) P ( m 1 ) \propto P (m 1 ∣ p) \cdot P (p) = p m 1 (1 - p) m 2 \cdot p a - 1 ( 1 - p ) b - 1 \int 1 0 p a - 1 ( 1 - p ) b - 1 d p \propto p m 1 (1 - p) m 2 \cdot p a - 1 (1 - p) b - 1 = p a + m 1 - 1 (1 - p) b + m 2 - 1

$\begin{matrix} P\left ( p\mid m_1 \right )=\frac{P\left ( m_1\mid p \right )\cdot P\left ( p \right )}{P\left ( m_1 \right )}\\ \propto P\left ( m_1\mid p \right )\cdot P\left ( p \right )\\ =p^{m_1}\left ( 1-p \right )^{m_2}\cdot \frac{p^{a-1}\left ( 1-p \right )^{b-1}}{\int_{0}^{1}p^{a-1}\left ( 1-p \right )^{b-1}dp}\\ \propto p^{m_1}\left ( 1-p \right )^{m_2}\cdot p^{a-1}\left ( 1-p \right )^{b-1}\\ =p^{a+m_1-1}\left ( 1-p \right )^{b+m_2-1} \end{matrix}$

由上可知，Beta分布是二项分布的共轭先验分布。

2、Dirichlet分布是多项式分布的共轭先验分布，即：

$D i r (p ⃗ ∣ α ⃗) + M u l t C o u n t (m ⃗) = D i r (p ⃗ ∣ α ⃗ + m ⃗)$ $Dir\left ( \vec{p}\mid \vec{\alpha } \right )+MultCount\left ( \vec{m} \right )=Dir\left ( \vec{p}\mid \vec{\alpha }+\vec{m} \right )$

我们对上式采用与Beta分布同样的证明方式，对于多项式分布，有下式成立：

P (m ⃗ ∣ p ⃗) = p m 1 1 p m 2 2 \dots p m k k

$P\left ( \vec{m}\mid \vec{p} \right )=p_1^{m_1}p_2^{m_2}\cdots p_k^{m_k}$

然而概率 $\vec{p}$ 服从的参数为 $\vec{\alpha }$ 的Dirichlet分布，即：

P (p ⃗ ∣ α ⃗) = p α 1 1 p α 2 2 \dots p α k k D ( α 1 , α 2 , \dots , α k )

$P\left ( \vec{p}\mid \vec{\alpha } \right )=\frac{p_1^{\alpha _1}p_2^{\alpha _2}\cdots p_k^{\alpha _k}}{D\left ( \alpha _1,\alpha _2,\cdots ,\alpha _k \right )}$

由贝叶斯定理可知：

P (p ⃗ ∣ m ⃗) = P ( m ⃗ ∣ p ⃗ ) \cdot P ( p ⃗ ) P ( m ⃗ ) \propto P (m ⃗ ∣ p ⃗) \cdot P (p ⃗) = p m 1 1 p m 2 2 \dots p m k k \cdot p α 1 1 p α 2 2 \dots p α k k D ( α 1 , α 2 , \dots , α k ) \propto p m 1 1 p m 2 2 \dots p m k k \cdot p α 1 1 p α 2 2 \dots p α k k = p m 1 + α 1 1 p m 2 + α 2 2 \dots p m k + α k k

$\begin{matrix} P\left ( \vec{p}\mid \vec{m} \right )=\frac{P\left ( \vec{m}\mid \vec{p} \right )\cdot P\left ( \vec{p} \right )}{P\left ( \vec{m} \right )}\\ \propto P\left ( \vec{m}\mid \vec{p} \right )\cdot P\left ( \vec{p} \right )\\ =p_1^{m_1}p_2^{m_2}\cdots p_k^{m_k}\cdot \frac{p_1^{\alpha _1}p_2^{\alpha _2}\cdots p_k^{\alpha _k}}{D\left ( \alpha _1,\alpha _2,\cdots ,\alpha _k \right )}\\ \propto p_1^{m_1}p_2^{m_2}\cdots p_k^{m_k}\cdot p_1^{\alpha _1}p_2^{\alpha _2}\cdots p_k^{\alpha _k}\\ =p_1^{m_1+\alpha _1}p_2^{m_2+\alpha _2}\cdots p_k^{m_k+\alpha _k} \end{matrix}$

由此可知，Dirichlet分布是多项式分布的共轭先验分布。

二、文本建模

对于一篇文章，是文章中出现的次的过程，在文章中，我们已经知道每个词出现的概率，则在省城文章的过程中，我们在词库中根据概率取出每个词，形成一篇文章。

1、Unigram Model

1.1、频率派

上述的过程说明了最简单的文本是如何产生的，我们对上述的过程数学化，假设：

词库中(即对所有文档中的词去停用词)共有 $V$ 个词： $v_1,v_2,\cdots ,v_V$ ；
词库中每一个词出现的次数记为： $n_1,n_2,\cdots ,n_V$ ，所有词出现的总次数为 $N$ ；
每个词对用的概率记为： $\vec{p}=\left \{ p_1,p_2,\cdots ,p_V \right \}$ 。

假设有 $m$ 篇文档，记为 $W=\left ( \vec{w}_1,\vec{w}_2,\cdots ,\vec{w}_m \right )$ ，则整个文档的概率为：

P (W) = P (w ⃗ 1, w ⃗ 2, \dots, w ⃗ m)

$P\left ( W \right )=P\left ( \vec{w}_1,\vec{w}_2,\cdots ,\vec{w}_m \right )$

在这里，我们假设文档与文档之间是相互独立的，而且进一步词与词之间也是相互独立的——词袋模型(Bag-of-words)。词袋模型表名词的顺序是无关紧要。基于这样的假设后上述的概率可以表示为：

P (W) = P (w ⃗ 1) P (w ⃗ 2) \dots P (w ⃗ m)

$P\left ( W \right )=P\left ( \vec{w}_1 \right )P\left ( \vec{w}_2 \right )\cdots P\left ( \vec{w}_m \right )$

对所有的这 $m$ 篇文档中，词 $v_i$ 出现的次数为 $n_i$ ，由于文档与文档之间是相互独立的，且词与词之间也是相互独立的，则对于所有的文档集 $W$ ，我们将相同的词记在一起，即对于词 $v_i$ ，记为总共出现的次数为 $n_i$ 。从词库中选择每个词的过程满足多项式分布，总共需要从词库中抽取 $N$ 次，则全体文档的概率为：

P (W) = P (w ⃗ 1) P (w ⃗ 2) \dots P (w ⃗ m) = \prod k = 1 N \prod i = 1 V p n i i

$\begin{matrix} P\left ( W \right )=P\left ( \vec{w}_1 \right )P\left ( \vec{w}_2 \right )\cdots P\left ( \vec{w}_m \right )\\ =\prod_{k=1}^{N}\prod_{i=1}^{V}p_i^{n_i} \end{matrix}$

至此，已经计算出全部文档的联合概率，但是对于每个词被选择的概率 $p_i$ 是一个未知数，一个很重要的任务就是估计上式中的每个词被选择的概率，通常使用的方法是使用最大似然估计的方法：

取上式的log似然函数：

l o g (P (W)) = N \cdot \sum i = 1 V n i \cdot l o g (p i)

$log\; \left ( P\left ( W \right ) \right )=N\cdot \sum_{i=1}^{V}n_i\cdot log\left ( p_i \right )$

对上述似然函数取最大值，即对每个概率值 $p_i$ 求导数：

最终，可以求得参数 $p_i$ 的估计值：

p i = n i N

$p_i=\frac{n_i}{N}$

1.2、贝叶斯派

对于贝叶斯派来说，其并不认同上述的求解参数值估计的方法，贝叶斯思维认为，一切的参数都是随机变量，因此上述的选择每个词的概率不是一个确定的值，而是一个随机变量，随机变量就应该服从一个分布。因此参数 $\vec{p}$ 是由分布 $P\left ( \vec{p} \right )$ 决定的，该分布称为先验分布。则上述的过程就变成了如下的两个过程：

首先由先验分布 $P\left ( \vec{p} \right )$ 得到参数的样本 $\vec{p}$ ；
由参数 $\vec{p}$ 生成文档。

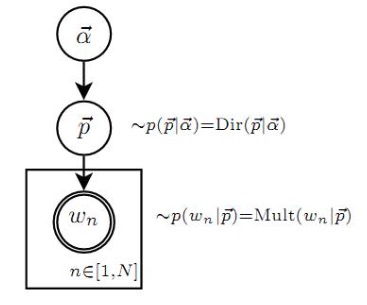
上述的过程，可以由下面的概率图模型表示：

这里写图片描述

依据上述的观点，则文档的概率可以表示为：

P (W) = \int P (W ∣ p ⃗) \cdot P (p ⃗) d p ⃗

$P\left ( W \right )=\int P\left ( W\mid \vec{p} \right )\cdot P\left ( \vec{p} \right )d\vec{p}$

此处的 $P\left ( \vec{p} \right )$ 称为先验分布，已知 $P\left ( W\mid \vec{p} \right )$ 服从多项式分布，由上述的共轭分布的知识可知：

多项式分布的共轭分布是Dirichlet分布。

因此对于先验分布 $P\left ( \vec{p} \right )$ 可以选择为Dirichlet分布：

D i r (p ⃗ ∣ α ⃗) = 1 Δ ( α ⃗ ) \prod i = 1 V p α i - 1 i

$Dir\left ( \vec{p}\mid \vec{\alpha } \right )=\frac{1}{\Delta \left ( \vec{\alpha } \right )}\prod_{i=1}^{V}p_i^{\alpha _i-1}$

其中， $\vec{\alpha }=\left ( \alpha _1,\alpha _2,\cdots ,\alpha _V \right )$ ， $\Delta \left ( \vec{\alpha } \right )$ 称为归一化因子：

Δ (α ⃗) = \int \prod i = 1 V p α i - 1 i d p ⃗

$\Delta \left ( \vec{\alpha } \right )=\int \prod_{i=1}^{V}p_i^{\alpha _i-1}d\vec{p}$

由共轭分布的知识可知：

先验分布为Dirichlet分布+多项分布的数据知识=后验分布为Dirichlet分布

$D i r (p ⃗ ∣ α ⃗) + M u l t C o u n t (n ⃗) = D i r (p ⃗ ∣ α ⃗ + n ⃗)$ $Dir \left ( \vec{p}\mid \vec{\alpha } \right )+MultCount\left ( \vec{n} \right )=Dir \left ( \vec{p}\mid \vec{\alpha }+\vec{n} \right )$

基于上述的共轭分布的性质，已知了参数 $\vec{p}$ 的先验分布为 $Dir \left ( \vec{p}\mid \vec{\alpha } \right )$ ，对于每个词出现的次数的统计服从多项式分布，则可以通过上述的性质得到后验分布：

P (p ⃗ ∣ W, α ⃗) = D i r (p ⃗ ∣ n ⃗ + a ⃗) = 1 Δ ( n ⃗ + a ⃗ ) \prod i = 1 V p n i + α i - 1 i

$P\left ( \vec{p}\mid W,\vec{\alpha } \right )=Dir\left ( \vec{p}\mid \vec{n}+\vec{a} \right )\\=\frac{1}{\Delta \left ( \vec{n}+\vec{a} \right )}\prod_{i=1}^{V}p_i^{n_i+\alpha _i-1}$

为了求得后验分布中的参数 $\vec{p}$ ，可以使用其均值来估计每一个参数，即：

E (p ⃗) = (n 1 + α 1 \sum V i = 1 ( n i + α i ), n 2 + α 2 \sum V i = 1 ( n i + α i ), \dots, n V + α V \sum V i = 1 ( n i + α i ))

$E\left ( \vec{p} \right )=\left ( \frac{n_1+\alpha _1}{\sum_{i=1}^{V}\left ( n_i+\alpha _i \right )},\frac{n_2+\alpha _2}{\sum_{i=1}^{V}\left ( n_i+\alpha _i \right )},\cdots , \frac{n_V+\alpha _V}{\sum_{i=1}^{V}\left ( n_i+\alpha _i \right )} \right )$

即：

p^i = n i + α i \sum V i = 1 ( n i + α i )

$\hat{p}_i=\frac{n_i+\alpha _i}{\sum_{i=1}^{V}\left ( n_i+\alpha _i \right )}$

对于整个文本的概率：

P (W ∣ α ⃗) = \int P (W ∣ p ⃗) \cdot P (p ⃗ ∣ α ⃗) d p ⃗

$P\left ( W\mid \vec{\alpha } \right )=\int P\left ( W\mid \vec{p} \right )\cdot P\left ( \vec{p}\mid \vec{\alpha } \right )d\vec{p}$

由于 $P\left ( W\mid \vec{p} \right )$ 服从多项式分布，而 $P\left ( \vec{p}\mid \vec{\alpha } \right )$ 服从的Dirichlet分布，则上式可以表示成：

P (W ∣ α ⃗) = \int \prod i = 1 V p n i i \cdot D i r (p ⃗ ∣ α ⃗) d p ⃗ = \int \prod i = 1 V p n i i \cdot 1 Δ ( α ⃗ ) \prod i = 1 V p α i - 1 i d p ⃗ = 1 Δ ( α ⃗ ) \int \prod i = 1 V p n i + α i - 1 i d p ⃗

$\begin{matrix} P\left ( W\mid \vec{\alpha } \right )=\int \prod_{i=1}^{V}p_i^{n_i}\cdot Dir\left ( \vec{p}\mid \vec{\alpha } \right )d\vec{p}\\ =\int \prod_{i=1}^{V}p_i^{n_i}\cdot \frac{1}{\Delta \left ( \vec{\alpha } \right )}\prod_{i=1}^{V}p_i^{\alpha _i-1}d\vec{p}\\ =\frac{1}{\Delta \left ( \vec{\alpha } \right )}\int \prod_{i=1}^{V}p_i^{n_i+\alpha _i-1}d\vec{p} \end{matrix}$

而已知： $\Delta \left ( \vec{\alpha } \right )=\int \prod_{i=1}^{V}p_i^{\alpha _i-1}d\vec{p}$ ，则上式可以表示成：

P (W ∣ α ⃗) = Δ ( n ⃗ + α ⃗ ) Δ ( α ⃗ )

$P\left ( W\mid \vec{\alpha } \right )=\frac{\Delta \left ( \vec{n}+\vec{\alpha } \right )}{\Delta \left ( \vec{\alpha } \right )}$

2、概率主题模型

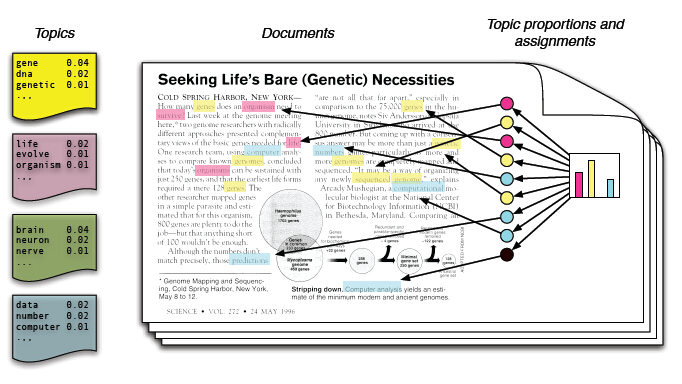
前面对文档的生成方式做了简单的介绍，其实在写文章的过程中，每一篇文章都会有一些主题，表示这篇文章主要讲的是关于哪方面的文章，如本篇文章主要是在介绍贝叶斯，LDA等等，而文章的基本组成单元式词，文章的主题则主要表现在词在不同组题的分布上，每一个词是在这些确定的主题上产生的，具体的如下图所示：

这里写图片描述

文章的主题最终体现在词在每个主题的分布上。在写文章的过程中，首先我们需要做的是确定文章的主题，在确定了文章的主题的前提下，我们产生每一个词，从而构成了整篇文章。

如果要写一篇文章，我们往往是先确定其主题，比如这篇文章是写社会的，还是写的技术类的，或者游记类的，在主题确定的条件下，如要写一篇关于机器学习方面的文章，在确定了主题的条件下，会谈及到损失函数，模型，神经网络，深度学习等等，每个词在这篇文章中的比重会有所不同。这便是文章的生成过程，即：

一篇文章，通常是由多个主题构成的，而每个主题大概可以用于该主题相关的频率最高的一些词来描述。

在上面们提及到一篇文章的生成过程，即：

对于文章选择主题
每个主题下对词汇的选择

2.1、频率派

频率派的观点是选择每个主题的概率和根据主题选择具体词的概率都是具体的值，根据上述的概率主题模型的思想，我们假设文档集中有 $M$ 篇文档，每一篇文章对应的主题的概率为： $\vec{\theta} _m, m\in \left [ 1,M \right ]$ ，在选定了文章的主题后，对于一篇文章，可能会有几个主题，此时，在主题确定的条件下，选择每个主题对应的词，对于第 $m$ 篇文章中的第 $n$ 个词，有其所属主题的编号 $z_{m,n}$ ，假设有 $K$ 个主题，在每个主题下选择词的概率为： $\vec{\varphi} _1,\vec{\varphi} _2,\cdots ,\vec{\varphi} _K$ ，在对应的第 $k$ 个主题下依据概率 $\vec{\varphi }_k$ 选择词。

注意：这里的文档与文档之间是相互独立的，同一个文档中的词与词之间也是相互独立的。

因此，上述过程中很多步骤是可以合并在一起的，同样，我们有如下的假设：

词库中(即对所有文档中的词去停用词)共有 $V$ 个词： $v_1,v_2,\cdots ,v_V$ ；
词库中每一个词出现的次数记为： $n_1,n_2,\cdots ,n_V$ ，所有词出现的总次数为 $N$ ；
第 $k$ 个主题下对应的词的概率为： $\vec{\varphi }_k=\left \{ \varphi _{k,1},\varphi _{k,2},\cdots ,\varphi _{k,V} \right \}$ ，其中 $k\in \left [ 1,K \right ]$ ；
第 $m$ 篇文档对应的主题的概率记为： $\vec{\theta }_m=\left \{ \theta _{m,1},\theta _{m,2},\cdots ,\theta _{m,K} \right \}$ ，其中 $m\in \left [ 1,M \right ]$ ；
对于每一篇文章中对应的词所属主题的编号为： $z_{m,n}$ 。

则对于第 $m$ 篇文档 $d_m$ 中的每一个词的生成概率为：

P (w ∣ d m) = \sum z = 1 K P (w ∣ z) P (z ∣ d m)

$P\left ( w\mid d_m \right )=\sum_{z=1}^{K}P\left ( w\mid z \right )P\left ( z\mid d_m \right )$

其中 $P\left ( z\mid d_m \right )$ 表示的是在每一篇文章对应的主题的编号，可以由 $\theta _{m,z}$ 表示； $P\left ( w\mid z \right )$ 表示的是在主题编号确定的条件下选择词的概率，可以由 $\varphi _{z,w}$ ，因此上式可以表示成：

P (w ∣ d m) = \sum z = 1 K φ z, w \cdot θ m, z

$P\left ( w\mid d_m \right )=\sum_{z=1}^{K}\varphi _{z,w}\cdot \theta _{m,z}$

由于在文档中词与词之间是相互独立的，因此对于一篇文档，其生成概率为：

P (w ⃗ ∣ d m) = \prod i = 1 N m \sum z = 1 K P (w i ∣ z) P (z ∣ d m) = \prod i = 1 N m \sum z = 1 K φ z, w i \cdot θ m, z

$\begin{matrix} P\left ( \vec{w}\mid d_m \right )=\prod_{i=1}^{N_m}\sum_{z=1}^{K}P\left ( w_i\mid z \right )P\left ( z\mid d_m \right )\\ =\prod_{i=1}^{N_m}\sum_{z=1}^{K}\varphi _{z,w_i}\cdot \theta _{m,z} \end{matrix}$

2.2、贝叶斯派

上面介绍的思路中，对于文档选择主题的概率以及依据主题选择每一个词的概率都是固定的数，对于贝叶斯派来说，这是无法接受的，贝叶斯派认为所有的值都是随机变量，因此，在文档对应的主题以及依据指定的主题选择每一个词的概率都服从特定的分布。因此上述的过程可以通过如下的概率图模型表示：

该图可以分解成如下的两个部分：

1、 $\vec{\alpha }\rightarrow \vec{\theta }_m\rightarrow z_{m,n}$ ，表示的是对于第 $m$ 篇文档，我们首先根据参数 $\vec{\alpha }$ 计算出其对应的主题的概率 $\vec{\theta }_m$ ，然后生成该文档中的第 $n$ 个词对应的主题的编号 $z_{m,n}$ ；
2、 $\vec{\beta }\rightarrow \vec{\varphi }_k\rightarrow w_{m,n}\mid k=z_{m,n}$ ，表示的是根据参数 $\vec{\beta }$ 计算出在主题编号确定的条件下主题对应的词的概率，依据这个概率选择出每个词。

对于上述过程中的两个阶段，其中从文档的主题的概率到词对应主题的编号服从的是多项式分布，由上述的共轭先验分布的知识可以知道：

多项式分布的共轭分布是Dirichlet分布。

可以选择 $\vec{\theta }_m$ 是服从参数为 $\vec{\alpha }$ 的Dirichlet分布，同样，我们可以选择 $\vec{\varphi }_k$ 是服从参数为 $\vec{\beta }$ 的Dirichlet分布。

对于整个文档集来说，文档与文档之间是相互独立的，单个文档中词与词之间也是相互独立的，因此上述的两个过程我们可以分解成如下的两个过程：

首先对于 $M$ 篇文档生成其对应的词对应的主题的编号
对于 $K$ 个主题，生成所有的文本

有了上述的两个过程的分解，对于整个文档集，我们可以得到下述的生成概率：

P (W, Z ∣ α ⃗, β ⃗) = P (W ∣ Z, β ⃗) \cdot P (Z ∣ α ⃗)

$P\left ( W,Z\mid \vec{\alpha },\vec{\beta } \right )=P\left ( W\mid Z,\vec{\beta } \right )\cdot P\left ( Z\mid \vec{\alpha } \right )$

其中， $P\left ( W\mid Z,\vec{\beta } \right )$ 表示的是在文章主题确定的条件下生成词的概率， $P\left ( Z\mid \vec{\alpha } \right )$ 表示的是文档对应主题的概率。

对于上述的第一个过程有：

P (z ⃗ m ∣ α ⃗) = \int P (z ⃗ m ∣ θ ⃗ m) \cdot P (θ ⃗ m ∣ α ⃗) d θ ⃗ m

$P\left ( \vec{z}_m\mid \vec{\alpha } \right )=\int P\left ( \vec{z}_m\mid \vec{\theta }_m \right )\cdot P\left ( \vec{\theta }_m\mid \vec{\alpha } \right )d\vec{\theta }_m$

已知 $P\left ( \vec{z}_m\mid \vec{\theta }_m \right )$ 服从的是多项式分布，而 $P\left ( \vec{\theta }_m\mid \vec{\alpha } \right )$ 服从的是Dirichlet分布，因此，上式可以转换成为：

P (z ⃗ m ∣ α ⃗) = \int \prod k = 1 K θ n k m, k \cdot D i r (θ ⃗ m ∣ α ⃗) d θ ⃗ m = \int \prod k = 1 K θ n k m, k \cdot 1 Δ ( α ⃗ ) \prod k = 1 K θ α k - 1 m, k d θ ⃗ m = 1 Δ ( α ⃗ ) \int \prod k = 1 K θ n k + α k - 1 m, k d θ ⃗ m = Δ ( n ⃗ m + α ⃗ ) Δ ( α ⃗ )

$\begin{matrix} P\left ( \vec{z}_m\mid \vec{\alpha } \right )=\int \prod_{k=1}^{K}\theta _{m,k}^{n_k}\cdot Dir\left ( \vec{\theta }_m\mid \vec{\alpha } \right )d\vec{\theta }_m\\ =\int \prod_{k=1}^{K}\theta _{m,k}^{n_k}\cdot \frac{1}{\Delta \left ( \vec{\alpha } \right )}\prod_{k=1}^{K}\theta _{m,k}^{\alpha _k-1}d\vec{\theta }_m\\ =\frac{1}{\Delta \left ( \vec{\alpha } \right )}\int \prod_{k=1}^{K}\theta _{m,k}^{n_k+\alpha _k-1}d\vec{\theta }_m\\ =\frac{\Delta \left ( \vec{n}_m+\vec{\alpha } \right )}{\Delta \left ( \vec{\alpha } \right )} \end{matrix}$

其中， $\vec{n}_m=\left ( n_m^{\left ( 1 \right )},n_m^{\left ( 2 \right )},\cdots ,n_m^{\left ( K \right )} \right )$ ， $n_m^{\left ( k \right )}$ 表示的是第 $m$ 篇文档中属于第 $k$ 个主题的词的个数。则对于所有的 $M$ 篇文档有：

P (Z ∣ α ⃗) = \prod m = 1 M P (z ⃗ m ∣ α ⃗) = \prod m = 1 M Δ ( n ⃗ m + α ⃗ ) Δ ( α ⃗ )

$P\left ( Z\mid \vec{\alpha } \right )=\prod_{m=1}^{M}P\left ( \vec{z}_m\mid \vec{\alpha } \right )=\prod_{m=1}^{M}\frac{\Delta \left ( \vec{n}_m+\vec{\alpha } \right )}{\Delta \left ( \vec{\alpha } \right )}$

对于第二个过程，有下式成立：

P (w ⃗ k ∣ z ⃗ k, β ⃗) = \int P (w ⃗ k ∣ φ ⃗ k) \cdot P (φ ⃗ k ∣ z ⃗ k, β ⃗) d φ ⃗ k

$P\left ( \vec{w}_{k}\mid \vec{z}_{k}, \vec{\beta } \right )=\int P\left ( \vec{w}_k\mid \vec{\varphi }_k \right )\cdot P\left ( \vec{\varphi }_k\mid \vec{z}_{k}, \vec{\beta } \right )d\vec{\varphi }_k$

其中， $P\left ( \vec{w}_k\mid \vec{\varphi }_k \right )$ 服从的是多项式分布，而 $P\left ( \vec{\varphi }_k\mid \vec{z}_{k}, \vec{\beta } \right )$ 服从的是Dirichlet分布，则上式可以转化为：

P (w ⃗ k ∣ z ⃗ k, β ⃗) = \int \prod v = 1 V φ n v k, v \cdot D i r (φ ⃗ k ∣ β ⃗) d φ ⃗ k = \int \prod v = 1 V φ n v k, v \cdot 1 Δ ( β ⃗ ) \prod v = 1 V φ β v - 1 k, v d φ ⃗ k = 1 Δ ( β ⃗ ) \int \prod v = 1 V φ n v + β v - 1 k, v d φ ⃗ k = Δ ( n ⃗ k + β ⃗ ) Δ ( β ⃗ )

$\begin{matrix} P\left ( \vec{w}_{k}\mid \vec{z}_{k}, \vec{\beta } \right )=\int \prod_{v=1}^{V}\varphi _{k,v}^{n_v}\cdot Dir\left ( \vec{\varphi }_k\mid \vec{\beta } \right )d\vec{\varphi }_k\\ =\int \prod_{v=1}^{V}\varphi _{k,v}^{n_v}\cdot \frac{1}{\Delta \left ( \vec{\beta } \right )}\prod_{v=1}^{V}\varphi _{k,v}^{\beta _v-1}d\vec{\varphi }_k\\ =\frac{1}{\Delta \left ( \vec{\beta } \right )}\int \prod_{v=1}^{V}\varphi _{k,v}^{n_v+\beta _v-1}d\vec{\varphi }_k\\ =\frac{\Delta \left ( \vec{n}_k+\vec{\beta } \right )}{\Delta \left ( \vec{\beta } \right )} \end{matrix}$

其中， $\vec{n}_k=\left ( n_k^{\left ( 1 \right )},n_k^{\left ( 2 \right )},\cdots ,n_k^{\left ( V \right )} \right )$ ， $n_k^{\left ( v \right )}$ 表示的是属于第 $k$ 个主题的词中词 $v$ 的个数，对于有所的 $V$ 个词，有下面的公式成立：

P (W ∣ Z, β ⃗) = \prod k = 1 K P (w ⃗ k ∣ z ⃗ k, β ⃗) = \prod k = 1 K Δ ( n ⃗ k + β ⃗ ) Δ ( β ⃗ )

$P\left ( W\mid Z, \vec{\beta } \right )=\prod_{k=1}^{K}P\left ( \vec{w}_{k}\mid \vec{z}_{k}, \vec{\beta } \right )=\prod_{k=1}^{K}\frac{\Delta \left ( \vec{n}_k+\vec{\beta } \right )}{\Delta \left ( \vec{\beta } \right )}$

因此，对于整个文档，有：

P (W, Z ∣ α ⃗, β ⃗) = P (W ∣ Z, β ⃗) \cdot P (Z ∣ α ⃗) = \prod k = 1 K Δ ( n ⃗ k + β ⃗ ) Δ ( β ⃗ ) \cdot \prod m = 1 M Δ ( n ⃗ m + α ⃗ ) Δ ( α ⃗ )

$P\left ( W,Z\mid \vec{\alpha },\vec{\beta } \right )=P\left ( W\mid Z, \vec{\beta } \right )\cdot P\left ( Z\mid \vec{\alpha } \right )=\prod_{k=1}^{K}\frac{\Delta \left ( \vec{n}_k+\vec{\beta } \right )}{\Delta \left ( \vec{\beta } \right )}\cdot \prod_{m=1}^{M}\frac{\Delta \left ( \vec{n}_m+\vec{\alpha } \right )}{\Delta \left ( \vec{\alpha } \right )}$

3、LDA训练——Gibbs采样

3.1、Markov Chain的相关概念

MCMC(Markov Chain Monte Carlo)和Gibbs采样算法是用来生成样本的随机模拟方法，Gibbs采样算法是LDA中参数求解的一种很有效的方法，想要理解Gibbs采样，必须了解以下的几个概念：

1、马尔可夫链

马尔可夫链的数学表示如下所示：

P (X t + 1 = x ∣ X t, X t - 1, \dots) = P (X t + 1 = x ∣ X t)

$P\left ( X_{t+1}=x\mid X_t,X_{t-1},\cdots \right )=P\left ( X_{t+1}=x\mid X_t \right )$

上述公式的含义是由状态 $X_t$ 到状态 $X_{t+1}$ 只与状态 $X_t$ 有关，而与之前的状态无关。

2、马氏链的平稳分布

如果一个非周期马氏链具有转移概率矩阵为 $P$ ，且它的任何两个状态是连通的，那么 $\lim_{n\rightarrow \infty }P_{ij}^n$ 存在且与 $i$ 无关，记 $\lim_{n\rightarrow \infty }P_{ij}^n＝\pi \left ( j \right )$ ，我们有：

lim n \to \infty P n i j = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ π (1) π (1) \dots π (1) \dots π (2) π (2) \dots π (2) \dots \dots \dots \dots \dots \dots π (j) π (j) \dots π (j) \dots \dots \dots \dots \dots \dots ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥

$\lim_{n\rightarrow \infty }P_{ij}^n=\begin{bmatrix} \pi \left ( 1 \right ) & \pi \left ( 2 \right ) & \cdots & \pi \left ( j \right ) &\cdots \\ \pi \left ( 1 \right ) & \pi \left ( 2 \right ) & \cdots & \pi \left ( j \right ) &\cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \\ \pi \left ( 1 \right ) & \pi \left ( 2 \right ) & \cdots & \pi \left ( j \right ) & \cdots \\ \cdots & \cdots & \cdots & \cdots & \cdots \end{bmatrix}$

π (j) = \sum i = 0 \infty π (i) P i j

$\pi \left ( j \right )=\sum_{i=0}^{\infty }\pi \left ( i \right )P_{ij}$

c. $\pi$ 是方程 $\pi P=\pi$ 的唯一非负解，其中：

π = [π (1), π (2), \dots, π (j), \dots]

$\pi =\left [ \pi \left ( 1 \right ),\pi \left ( 2 \right ),\cdots ,\pi \left ( j \right ),\cdots \right ]$

\sum i = \infty π i = 1

$\sum_{i=}^{\infty }\pi _i=1$

$\pi$ 称为马氏链的平稳分布。

3、细致平稳条件

如果非周期马氏链的转移矩阵 $P$ 和分布 $\pi \left ( x \right )$ 满足：

π (i) P i j = π (j) P j i, \forall i, j

$\pi \left ( i \right )P_{ij}=\pi \left ( j \right )P_{ji},\; \forall i,j$

则 $\pi \left ( x \right )$ 是马氏链的平稳分布，上式被称为细致平稳条件。

以上三条定理摘自参考文献1。

3.2、Gibbs采样

现在我们假设平面上有一些点，这些点服从概率分布 $P\left ( x,y \right )$ ，取其中两个点 $A$ 和 $B$ ，这两个点的横坐标一致，记为 $x$ ，且每个点的概率由其坐标决定，即点 $A$ 的概率为 $P\left ( x,y_A \right )$ ，同样，点 $B$ 的概率为 $P\left ( x,y_B \right )$ 。由点 $A$ 转移到点 $B$ 的概率为 $P\left ( y_B\mid x\right )$ ，同样，由点 $B$ 转移到点 $A$ 的概率为 $P\left ( y_A\mid x\right )$ ，则有如下的公式成立：

P (x, y A) \cdot P (y B ∣ x) = P (x) \cdot P (y A ∣ x) \cdot P (y B ∣ x)

$P\left ( x,y_A \right )\cdot P\left ( y_B\mid x \right )=P\left ( x \right )\cdot P\left ( y_A\mid x \right )\cdot P\left ( y_B\mid x \right )$

P (x, y B) \cdot P (y A ∣ x) = P (x) \cdot P (y B ∣ x) \cdot P (y A ∣ x)

$P\left ( x,y_B \right )\cdot P\left ( y_A\mid x \right )=P\left ( x \right )\cdot P\left ( y_B\mid x \right )\cdot P\left ( y_A\mid x \right )$

由上式可得：

P (x, y B) \cdot P (y A ∣ x) = P (x, y A) \cdot P (y B ∣ x)

$P\left ( x,y_B \right )\cdot P\left ( y_A\mid x \right )=P\left ( x,y_A \right )\cdot P\left ( y_B\mid x \right )$

由上式可以知道，如果以 $P\left ( y\mid x \right )$ 作为任意两点之间的转移概率，那么任何两点之间的转移满足细致平稳条件，前提是两点之间的转移概率的条件是相同的，即在两点之间转移，必须保证这两点的其中一个维度是相同的，如上式中的横坐标 $x$ 是相同的。

由此，我们可以得到Gibbs采样的通俗理解方式，即已知样本 $\left ( x_0,y_0 \right )$ ，我们可以利用 $P\left ( x\mid y_0 \right )$ 产生 $\left ( x_1,y_0 \right )$ ，同样，可以由 $P\left ( y\mid x_1 \right )$ 产生 $\left ( x_1,y_1 \right )$ ，依次，我们便可以得到样本序列：

$\left ( x_0,y_0 \right ),\left ( x_1,y_0 \right ),\left ( x_1,y_1 \right ),\left ( x_2,y_1 \right ),\cdots$

当马氏链收敛后，得到的样本：

(x t, y t), (x t + 1, y t), (x t + 1, y t + 1), \dots

$\left ( x_t,y_t \right ),\left ( x_{t+1},y_t \right ),\left ( x_{t+1},y_{t+1} \right ),\cdots$ 便是服从概率为

P(x,y) $P\left ( x,y \right )$ 的样本。

上述过程可由下面的形式描述：

这里写图片描述

这样的情况很容易推广到多维的情况：

这里写图片描述

上述两张图来自参考文献1。

3.3、LDA训练

对于LDA，我们希望的是能够计算在词确定的条件下计算其所属主题的概率，即如下的条件分布：

P (Z ∣ W, α ⃗, β ⃗)

$P\left ( Z\mid W, \vec{\alpha },\vec{\beta } \right )$

由于主题 $Z$ 是一个隐含的变量，我们通过如上的Gibbs采样去求解，由贝叶斯公式可知：

P (z i = k ∣ Z - i) \propto P (z i = k, w i = t ∣ Z - i, W - i)

$P\left ( z_i=k\mid Z_{-i} \right )\propto P\left ( z_i=k,w_i=t\mid Z_{-i},W_{-i} \right )$

而已知：

P (θ ⃗ m ∣ Z - i, W - i) = D i r (θ ⃗ m ∣ n ⃗ m, - i + α ⃗)

$P\left ( \vec{\theta }_m\mid Z_{-i},W_{-i} \right )=Dir\left ( \vec{\theta }_m\mid \vec{n}_{m,-i}+\vec{\alpha } \right )$

P (φ ⃗ k ∣ Z - i, W - i) = D i r (φ ⃗ k ∣ n ⃗ k, - i + β ⃗)

$P\left ( \vec{\varphi }_k\mid Z_{-i},W_{-i} \right )=Dir\left ( \vec{\varphi }_k\mid \vec{n}_{k,-i}+\vec{\beta } \right )$

则可以推出下面的式子：

P (z i = k ∣ Z - i, W) \propto P (z i = k, w i = t ∣ Z - i, W - i) = \int P (z i = k, w i = t, θ ⃗ m, φ ⃗ k ∣ Z - i, W - i) d θ ⃗ m d φ ⃗ k = \int P (z i = k, θ ⃗ m ∣ Z - i, W - i) \cdot P (w i = t, φ ⃗ k ∣ Z - i, W - i) d θ ⃗ m d φ ⃗ k = \int P (z i = k ∣ θ ⃗ m) P (θ ⃗ m ∣ Z - i, W - i) \cdot P (w i = t ∣ φ ⃗ k) P (φ ⃗ k ∣ Z - i, W - i) d θ ⃗ m d φ ⃗ k \int P (z i = k ∣ θ ⃗ m) D i r (θ ⃗ m ∣ n ⃗ m, - i + α ⃗) d θ ⃗ m \cdot \int P (w i = t ∣ φ ⃗ k) D i r (φ ⃗ k ∣ n ⃗ k, - i + β ⃗) d φ ⃗ k

$\begin{matrix} P\left ( z_i=k\mid Z_{-i},W \right )\propto P\left ( z_i=k,w_i=t\mid Z_{-i},W_{-i} \right )\\ =\int P\left ( z_i=k,w_i=t,\vec{\theta }_m,\vec{\varphi }_k\mid Z_{-i},W_{-i} \right )d\vec{\theta }_md\vec{\varphi }_k \\ =\int P\left ( z_i=k,\vec{\theta }_m\mid Z_{-i},W_{-i} \right )\cdot P\left ( w_i=t,\vec{\varphi }_k\mid Z_{-i},W_{-i} \right )d\vec{\theta }_md\vec{\varphi }_k\\ =\int P\left ( z_i=k\mid \vec{\theta }_m \right )P\left ( \vec{\theta }_m\mid Z_{-i},W_{-i} \right )\cdot P\left ( w_i=t\mid \vec{\varphi }_k \right )P\left (\vec{\varphi }_k\mid Z_{-i},W_{-i} \right )d\vec{\theta }_md\vec{\varphi }_k\\ \int P\left ( z_i=k\mid \vec{\theta }_m \right )Dir\left ( \vec{\theta }_m\mid \vec{n}_{m,-i}+\vec{\alpha } \right )d\vec{\theta }_m\cdot \int P\left ( w_i=t\mid \vec{\varphi }_k \right )Dir\left ( \vec{\varphi }_k\mid \vec{n}_{k,-i}+\vec{\beta } \right )d\vec{\varphi }_k \end{matrix}$

= \int θ m k D i r (θ ⃗ m ∣ n ⃗ m, - i + α ⃗) d θ ⃗ m \cdot \int φ k t D i r (φ ⃗ k ∣ n ⃗ k, - i + β ⃗) d φ ⃗ k = E (θ m k) \cdot E (φ k t) = θ m k^\cdot φ k t^

$\begin{matrix} =\int \theta _{mk}Dir\left ( \vec{\theta }_m\mid \vec{n}_{m,-i}+\vec{\alpha } \right )d\vec{\theta }_m\cdot \int \varphi _{kt}Dir\left ( \vec{\varphi }_k\mid \vec{n}_{k,-i}+\vec{\beta } \right )d\vec{\varphi }_k\\ =E\left ( \theta _{mk} \right )\cdot E\left ( \varphi _{kt} \right )\\ =\hat{\theta _{mk}}\cdot \hat{\varphi _{kt}} \end{matrix}$

在Dirichlet分布中，我们知道：

θ m k^＝ n ( k ) m , - i + α k \sum K k = 1 ( n ( k ) m , - i + α k )

$\hat{\theta _{mk}}＝\frac{n_{m,-i}^{\left ( k \right )}+\alpha _k}{\sum_{k=1}^{K}\left ( n_{m,-i}^{\left ( k \right )}+\alpha _k \right )}$

φ k t^＝ n ( t ) k , - i + β t \sum V t = 1 ( n ( t ) k , - i + β t )

$\hat{\varphi _{kt}}＝\frac{n_{k,-i}^{\left ( t \right )}+\beta _t}{\sum_{t=1}^{V}\left ( n_{k,-i}^{\left ( t \right )}+\beta _t \right )}$

因此有：

P (z i = k ∣ Z - i, W) \propto n ( k ) m , - i + α k \sum K k = 1 ( n ( k ) m , - i + α k ) \cdot n ( t ) k , - i + β t \sum V t = 1 ( n ( t ) k , - i + β t )

$P\left ( z_i=k\mid Z_{-i},W \right )\propto \frac{n_{m,-i}^{\left ( k \right )}+\alpha _k}{\sum_{k=1}^{K}\left ( n_{m,-i}^{\left ( k \right )}+\alpha _k \right )}\cdot \frac{n_{k,-i}^{\left ( t \right )}+\beta _t}{\sum_{t=1}^{V}\left ( n_{k,-i}^{\left ( t \right )}+\beta _t \right )}$

LDA的训练过程如下所示：

这里写图片描述

4、LDA推理

LDA推理的过程与LDA训练的过程类似，具体过程如下所示：

这里写图片描述

两张图来自参考文献1。

参考文献

1、LDA数学八卦

2、通俗理解LDA主题模型

3、零基础小白使用LDA模型

4、LDA理解以及源码分析(二)

5、Xuan-Hieu Phan and Cam-Tu Nguyen. GibbsLDA++: A C/C++ implementation of latent Dirichlet allocation (LDA), 2007

zhiyong_will

关注

12
点赞
踩
70

收藏

觉得还不错? 一键收藏
3
评论
简单易学的机器学习算法——Latent Dirichlet Allocation（理论篇）

引言LDA(Latent Dirichlet Allocation)称为潜在狄利克雷分布，是文本语义分析中比较重要的一个模型，同时，LDA模型中使用到了贝叶斯思维的一些知识，这些知识是统计机器学习的基础，这些知识点包括Gamma函数和分布，Beta函数和分布，Dirichlet函数和分布，贝叶斯定理，Gibbs采样等等。在接下来的文章，我们通过以下几个方面具体介绍LDA的核心思想：基础知
复制链接

扫一扫