从二叉查找树到平衡二叉树再到红黑树

最新推荐文章于 2024-09-21 00:07:02 发布

我的十六亩三分地

最新推荐文章于 2024-09-21 00:07:02 发布

阅读量2.8k

点赞数 1

分类专栏：数据结构/算法

本文链接：https://blog.csdn.net/workformywork/article/details/23517701

版权

数据结构/算法专栏收录该内容

7 篇文章 0 订阅

订阅专栏

本文详细介绍了二叉查找树的定义、插入与删除操作，接着探讨了平衡二叉树（AVL树）的概念及其插入节点后的平衡调整策略。进一步，文章深入讲解了红黑树的五个性质、插入节点的处理以及删除节点的调整，阐述了红黑树相较于平衡二叉树的优势。

摘要由CSDN通过智能技术生成

二叉查找树

定义：二叉查找树是一个二叉树结构，对于这个二叉树中的每一个节点X，它的左子树中的节点都小于X节点的关键字值，而右子树中的节点都大于X节点的关键字值。
二叉查找树也称作二叉排序树。

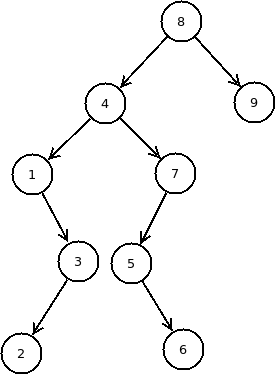
根据上面的定义，下面的一个二叉树就是一个二叉查找树：

可以看到，按照中序遍历这个二叉树可以得到一个有序递增的序列。

定义二叉查找树的结构

与二叉树类似，其定义代码如下：

typedef struct BSNode {
    char ch;
    struct BSNode *left, *right;
} BSNode, *BSTree;

插入

构建二叉查找树的过程就是一个递归(或迭代)调用插入操作的处理过程，类似于二叉树的构建，但是二叉查找树的插入则需要先找到合适的插入位置，然后再插入节点。如上图所示的二叉查找树，可以按照这个序列来插入：6、4、8、3、5、7、9，首先插入节点6，此时这个节点是根节点，然后插入节点4，从树根开始遍历找到节点6的左孩子的位置，再插入节点，依此类推。
这个插入节点的函数如下：


void insert(BSTree *T, char c) {
    if(*T == NULL) {
        *T = createBSNode(c);
    } else {
        if((*T)->ch > c) {
            insert(&((*T)->left), c);
        } else if((*T)->ch < c) {
            insert(&((*T)->right), c);
        } else {
            return;
        }
    }
}
/*创建节点函数*/
BSNode* createBSNode(char c) {
    BSNode *node = malloc(sizeof(BSNode));
    node->ch = c;
    node->left = NULL;
    node->right = NULL;
    return node;
}

在上面的代码中每次插入一个节点就先与二叉查找树的根节点比较，如果根节点为NULL，说明这个二叉查找树为空树，那么就直接插入这个一个节点，如果要插入的节点元素比根节点的元素小，那么就在根节点的左子树中找到合适的插入位置，如果插入节点的元素比根节点的元素大，则在根节点的右子树中找到合适的插入位置，否则这个带插入的节点的元素已经存在于这个二叉查找树中，那么直接返回。

删除

二叉查找树的节点删除过程较插入稍微复杂一些，因为删除一个节点时，需要考虑三种情况：

待删除的节点为叶子节点；
待删除的节点有一个子树为空；
待删除的节点的左右子树均不为空；

以下图为例：

对于情况1，只需要从二叉查找树中直接删除这个节点，调整其父节点的指针为NULL，如图中的节点2，6，9这三个节点，如果要删除节点2，直接将节点3的左孩子指针设置为NULL，然后删除节点2，对于情况2，只需要调整将待删除节点的父节点的指针，指向待删除节点的不为空的子树根节点，如图中的节点1，7， 3， 5，如果要删除节点3，直接将节点1的右孩子指针指向节点2，然后删除节点3，对于情况3，要保证删除节点之后，不改变二叉查找树的结构，所以删除节点后，树中元素的相对位置不能改变，如节点4和8，可以有以下三种方式，假设待删除节点为p：

使用p的左孩子代替p，p的右子树称为p的左子树的最右节点的右子树，如果要删除节点4，那么将节点8的左孩子指针指向节点1，然后节点7代表的子树成为节点3的右子树，这个结果所代表的树也为二叉查找树；
使用p的中序遍历的直接前驱代替p，然后删除p的直接前驱节点，如果要删除节点4，可以使用节点4的中序遍历的直接前驱节点3代替节点4，然后删除节点3；
使用p的中序遍历的直接后继代替p，然后删除p的直接后继节点，如果要删除节点4，可以使用节点4的中序遍历的直接后继节点5，代替节点4，然后删除节点5；

对于方式2和方式3，因为p的中序遍历的直接前驱或者直接后继节点至少有一个子树为空，所以使用p的中序遍历的直接前驱或者直接后继替换后，又将这个删除问题转化成上面3中情况中的情况1或者情况2。

基于上面的分析，删除节点的代码如下：

//删除节点
void deleteNode(BSNode *pre, BSNode *p) {
    if(pre->left == p) {
        pre->left = p->left != NULL ? p->left : p->right;
    } else {
        pre->right = p->left != NULL ? p->left : p->right;
    }
}

void delete(BSTree *T, char c) {
    BSNode *p, *pre, *preq, *q;
    p = *T;
    pre = p;
    while(p != NULL)  {
        if(p->ch == c) {
            if(p->left == NULL || p->right == NULL) {
                if(pre == p) {//删除根节点， 且根节点至少有一个子树为NULL
                    *T = p->left != NULL ? p->left : p->right;
                } else {//待删除节点至少有一个子树为NULL
                    deleteNode(pre, p);
                }
            } else {//待删除节点两个子树都不为NULL
                q = p->right;
                while(q->left != NULL) {//找到待删除节点按中序遍历的直接后继
                    pre = q;
                    q = q->left;
                }
                p->ch = q->ch;
                p = q;
                deleteNode(pre, p);
            }
            free(p);
            break;
        } else {
            pre = p;
            p = p->ch > c ? p->left : p->right;
        }
    }
}

有重复元素的二叉查找树

如果有重复元素插入或删除，可以为每个节点增加一个表示引用的成员ref，每次插入一个相同的节点，这个节点的ref++，每次删除一个相同的节点那么ref–，如果ref为0，那么就可以直接从二叉查找树中删除这个节点。

最大元素，最小元素

对于二叉排序树这样的特殊结构，求最小元素，可以从根节点开始，指针一路向左，知道找到整个二叉排序树的最左节点，同理最大元素就从根节点开始一路向右，知道找个最右节点。

平衡二叉树

平衡二叉树也称AVL树，得名于它的发明者G.M. Adelson-Velsky和E.M. Landis。
平衡二叉树本质上也是二叉查找树，只是它是一种特殊的二叉查找树，即树中任何节点的两个子树的高度最大差为1。下图所示的二叉查找树就是一个平衡二叉树：

这个平衡二叉树中，每个节点的左右子树高度之差都不超过1。

如果向上面的平衡二叉树中插入节点6，那么就破坏了节点8的平衡条件（节点5的平衡条件没有破坏），就需要对这个二叉树进行调整，使之重新称为一个平衡二叉树。根据二叉查找树的插入过程可知，在平衡二叉树中插入一个节点后，只有那些从插入点到根节点的路径上的节点的平衡条件可能被改变，因为只有这些节点的子树可能发生变化。所以在这条路径上找到第一个不平衡的节点，设为A节点，对这个节点进行调整即可使这个二叉树重新达到平衡，那么如何进行调整呢？平衡二叉树在插入一个节点后，变为不平衡二叉树主要分为四种情况：

左左情形，即在A的左孩子的左子树中插入一个节点；
左右情形，即在A的左孩子的右子树中插入一个节点；
右左情形，即在A的右孩子的左子树中插入一个节点；
右右情形，即在A的右孩子的右子树中插入一个节点；

对应于这四种情形，调整方式分别如下：
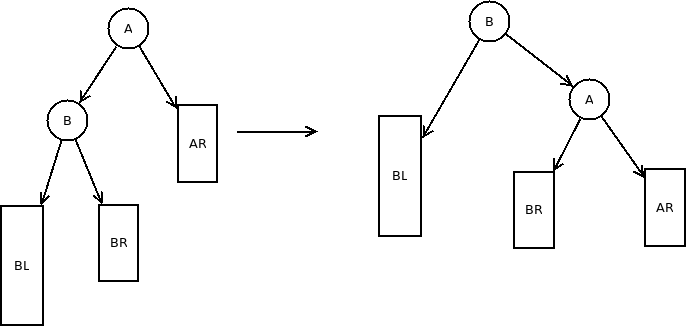
情形1，子树节点A的右子树AR高度为h-1，节点A的左子树根节点为B，节点B的左子树BL中插入一个节点后，高度变为h，节点B的右子树BR高度为h-1，这样节点A的左子树高度就为h+1，右子树的高度就为h-1，所以A节点就是第一个不平衡的节点，那么就要对A节点进行调整

调整的方式就是将A向右旋转，使得B节点成为根节点，A节点成为B节点的右子树根节点，B节点的右子树成为A的左子树，由于B < BR < A，所以这样旋转没有破坏二叉查找树的结构，由上面的旋转过程可以看出，在插入节点前，以A为根节点的树高度为h+1，插入节点后旋转之前，以A为根节点的树高度为h+2，旋转以后，以B为根节点的树高度为h+1，所以这个过程即将旋转以前B节点的左子树上移一层，A的右子树下移一层，这样整个子树的新高度恰恰与插入前的原树的高度相同。

情形2，子树节点A的右子树AR高度为h-1，节点A的左子树根节点为B，节点B的左子树BL高度为h-1，B的右子树根节点为节点C，C的左子树CL高度为h-2，右子树CR高度为h-1，这种情况下，节点A就是一个不平衡的节点，那么就需要对A进行调整，如下图：

调整的方式就是先将B节点向左旋转，使B节点成为C节点的左子树根节点，C节点成为A的左子树根节点，然后再将A节点向右旋转使A节点成为C节点的右子树根节点，在旋转完成后，C的左子树成为B的右子树，C的右子树成为A的左子树，这并没有破坏原二叉查找树的性质，在插入节点前，以A的根节点的子树高度为h+1，插入节点后旋转之前以A为根节点的子树高度为h+2，旋转之后，以C为根节点的子树高度为h+1，可见插入节点后进行旋转，没有改变子树的高度，其实整个旋转的过程是将C的高度为h-1的子树向上移了一层，而A的高度为h-1的子树向下移了一层，这样相对于插入节点之前，子树的高度并没有改变，所以对A节点进行旋转后，整个二叉树右达到平衡状态。

情形3，子树A的右孩子的左子树中插入一个节点，这与情形2是对称的，类似情形2旋转即可；

情形4，子树A的右孩子的右子树中插入一个节点，这与情形1是对称的，类似情形1旋转即可。

从上面的四种情形以看到，旋转后，相对于插入节点之前整个子树的高度不变，即把子树的高度恢复到插入前的水平。因此当平衡的二叉排序树因插入节点而失去平衡时，仅需对最小不平衡子树进行平衡旋转处理即可，因为经过旋转处理之后的子树深度和插入之前相同，因而不影响插入路径上所有祖先节点的平衡度。

根据上面的分析，实现平衡二叉树的相关算法，首先要对二叉查找树的结构进行改造，每个节点都加入一个平衡因子，所以平衡二叉树结构体的定义如下：

typedef struct BBSNode {
    char ch;
    short bf;//节点的平衡因子
    struct BBSNode *left, *right;
} BBSNode, *BBSTree;

平衡二叉树的插入算法如下：

/**
 * 向平衡二叉树T中插入元素为c的节点，如果插入节点则，返回1，否则返回0, 变量taller表示树是否长高了
 */
void insert(BBSTree *T, char c, int *taller) {
    if(*T == NULL) {
        *T = createBBSNode(c);
        *taller = 1;
    } else {
        if((*T)->ch > c) {
            insert(&((*T)->left), c, taller);
            if(*taller) {
                switch((*T)->bf) {
                    case 1: //左子树的比右子树高1，并且又插入一个节点，那么左子树比右子树高2
                        leftBanlace(T);
                        *taller = 0;
                        break;
                    case 0:
                        (*T)->bf = 1;
                        *taller = 1;
                        break;
                    case -1:
                        (*T)->bf = 0;
                        *taller = 0;
                        break;

                }
            }
        } else if((*T)->ch < c) {
            insert(&((*T)->right), c, taller);
            if(*taller) {
                switch((*T)->bf) {
                    case 1:
                        (*T)->bf = 0;
                        *taller = 0;
                        break;
                    case 0:
                        (*T)->bf = -1;
                        *taller = 1;
                        break;
                    case -1:
                        rightBalance(T);
                        *taller = 0;
                        break;
                }
            }
        } else {
            return;
        }
    } 
}

在上面的插入算法中，使用了leftBalance()函数和rightBalance()函数来对树进行平衡处理，插入节点后如果节点A的左子树比右子树高度高2，那么就对A进行左平衡处理，插入节点后，如果节点A的右子树比左子树高度高2，那么就对A进行右平衡处理，leftBanalce()和rightBalance()函数的实现代码如下：


void leftBanlace(BBSTree *T) {
    BBSNode *lc = (*T)->left;//使lc指向T的左孩子
    BBSNode *lcrc;
    switch(lc->bf) {
        case 1:
            //情形1，lc就成为这个子树的根节点，T成为lc的右孩子
            (*T)->bf = 0;
            lc->bf = 0;
            rightRotate(T);//将T节点向右旋转
            break;
        case -1:
            //情形2
            lcrc = lc->right;//lcrc指向lc的右孩子，用于设置旋转完成后各个节点的平衡因子
            switch(lcrc->bf) {
                case 1://lcrc的左子树高度为h-1，右子树高度为h-2
                    (*T)->bf = -1;
                    lc->bf = 0;
                    break;
                case 0:
                    (*T)->bf = 0;
                    lc->bf = 0;
                    break;
                case -1:
                    (*T)->bf = 0;
                    lc->bf = 1;
                    break;
            }
            lcrc->bf = 0;
            //leftRotate(&lc);
            leftRotate(&(*T)->left);
            rightRotate(T);
            break;
    }
}

void rightBalance(BBSTree *T) {
    BBSNode *rc = (*T)->right;
    BBSNode *rclc;
    switch(rc->bf) {
        case 1://情形4
            rclc = rc->left;
            switch(rclc->bf) {
                case 1:
                    (*T)->bf = 0;
                    rc->bf = -1;
                    break;
                case 0:
                    (*T)->bf = 0;
                    rc->bf = 0;
                    break;
                case -1:
                    (*T)->bf = 1;
                    rc->bf = 0;
                    break;
            }
            rclc->bf = 0;
            //rightRotate(&rc);
            rightRotate(&(*T)->right);
            leftRotate(T);
            break;
        case -1://情形3
            (*T)->bf = 0;
            rc->bf = 0;
            leftRotate(T);
            break;
    }
}

leftBalance()函数与rightBanalce()是对应的，leftBalance函数处理上面提到的情形1和情形2，rightBanalce函数处理情形3和情形4。对于leftBalance函数，以T为根节点的子树处于不平衡状态，其中T的左子树的高度比T的右子树的高度大2，所以首先使用指针lc指向T的左子树，然后利用lc.bf判断左子树与右子树的高度，如果lc.bf等于1，这就对应情形1，即T到lc的左子树这条路径的高度比T的右子树的高度大2，所以此时向右旋转T使用lc替代T节点成为整个子树的根节点，由于lc的右子树变为T的左子树，T变为lc的右子树，所以旋转的同时改变lc节点和T节点的平衡因子，同理可分析情形2，如果lc的右子树高度比lc的左子树高度大1，那么从T到lc再到lc的右子树这条路径的高度比T的右子树的高度大2，所以就要先向左旋转节点lc，然后旋转节点T，这样就使子树重新达到平衡状态。

红黑树

红黑树也是一种二叉查找树，但是在每个节点上都增加了一个颜色属性，颜色可以是红的(RED)，可以是黑的(BLACK)。
红黑树的五个性质：
1. 每个节点要么是红的要么是黑的
2. 根节点是黑的
3. 所有的叶子节点是黑的
4. 红节点的子节点一定是黑节点
5. 从任意一个节点到叶子节点所有路径上的黑节点数目相同。

通过这5条性质，对红黑树的每个节点的着色方式进行了限制，这样红黑树没有一条路径会比其他路径长处两倍，因此红黑树是接近平衡的。

插入一个节点，会破坏性质2或性质4，如果插入的节点是根节点，即原树是空树，那么会破坏性质2，如果插入的节点的父节点是红色节点，那么会破坏性质4，插入一个节点后，性质2和性质4之多有一个性质可能会被破坏。

红黑树的定义

由于每个节点需要保存一个颜色变量，而整个红黑树只有两种颜色，所以定义一个枚举类型NodeColor来代表红色和黑色，同时在红黑树中插入和删除节点时，可能会破坏红黑树的性质，从而需要对部分节点进行调整，为了方便的找到某个节点的父节点，所以在节点类型中定义一个指向父节点的指针parent，红黑树的节点定义如下：

typedef enum NodeColor {RED, BLACK} NodeColor;

typedef struct RBNode {
    char ch;
    struct RBNode *left,*right, *parent;
    NodeColor color;
} RBNode, *RBTree;

红黑树的节点插入

对于一棵红黑树，为了便于处理红黑树中的边界条件，定义一个哨兵节点NIL，这个节点定义为黑色的，其他四个值parent，left，right和ch设置为任意允许的值，红黑树中的每个节点如果其为新插入的节点，那么它的左右子树均指向这个哨兵节点NIL，此外红黑树的根节点的父节点也为哨兵节点NIL，如下图：

上图中最下面的节点就是哨兵节点，所有不指向孩子节点的指针都指向这个哨兵节点，并且根节点的parent指针也指向这个哨兵节点，这样红黑树中的所有节点都可以当作普通节点来看待。一般画红黑树都省掉这个哨兵节点，但是都默认会有这个节点，这样的红黑树就如下图所示：

插入节点时，新插入的节点的颜色规定为红色，这样插入新的节点后可能会破坏红黑树的性质。对于性质1，新插入的节点都是红色，所以不会破坏性质1，对于性质3，由于所有的也节点为哨兵节点NIL，所以性质3也不会破坏，对于性质5，由于新插入的节点为红色，不会改变任何路径上黑节点的个数，所以性质5也不会破坏。

当原红黑树的根节点为空，即为空树时，新插入节点会破坏性质2，当插入的节点的父节点为红色时，会破坏性质4。

在一棵红黑树中插入节点时，如果破坏了性质2和性质4，那么就需要对红黑树进行调整，与平衡二叉树类似，在调整的过程中需要也可能对节点进行旋转，但是考虑到红黑树的节点的颜色，也可能仅仅通过对节点颜色的调整就能将新的树调整为一棵红黑树。

如果破坏了性质2，则仅需对调整新插入的节点(根节点)为黑色即可；

如果破坏了性质4，则需要分6中情况对节点进行调整，但是其中有三种和另外三种情况是对称的，假设新插入的节点为z，其父节点为p，z的祖父节点为q，p的兄弟节点，即z的叔叔节点为y，下面分别就这6中情况进行讨论：

p为q的左孩子，且p的兄弟节点y为红节点；
p为q的左孩子，p的兄弟节点为黑节点，且y为p的右孩子；
p为q的左孩子，p的兄弟节点为黑节点，且y为p的左孩子；
p为q的右孩子，且p的兄弟节点y为红色节点；
p为q的右孩子，p的兄弟节点y为黑色，且y为p的左孩子；
p为q的右孩子，p的兄弟节点y为黑色，且y为p的右孩子

可以看到情况1，情况2，情况3分别与情况4，情况5，情况6对称。

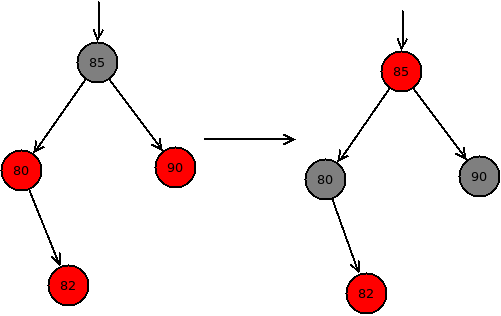
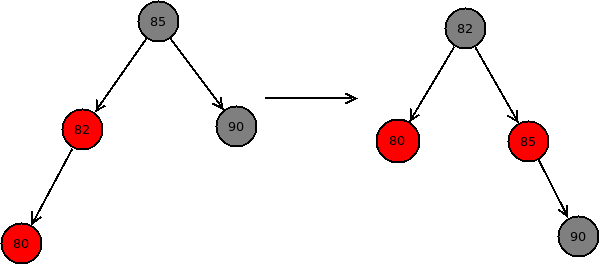
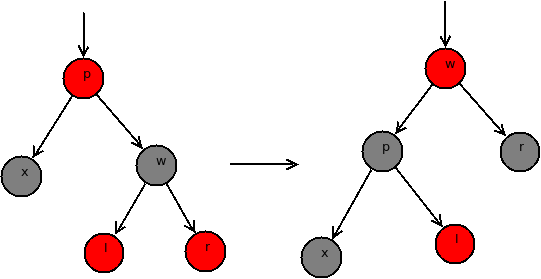
对于情况1，可以直接设置p节点和y节点为黑色，然后设置q为红色，这样以q为根节点的子树中到叶子节点的路径上的黑色节点的数目没有变化，因为q的两个子节点由红色变为黑色，而q节点由黑色变为红色，并且q节点的两棵子树的到叶子节点的路径上的黑色节点数目都增加1，如下图所示：

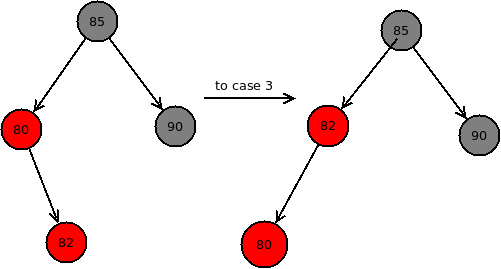
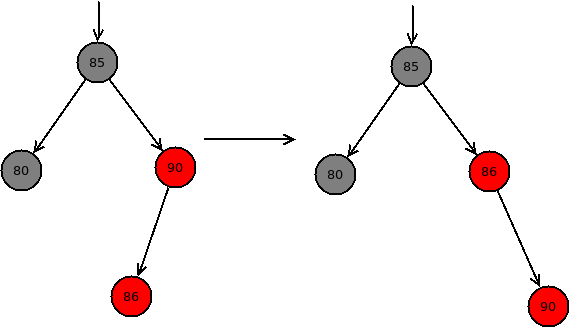
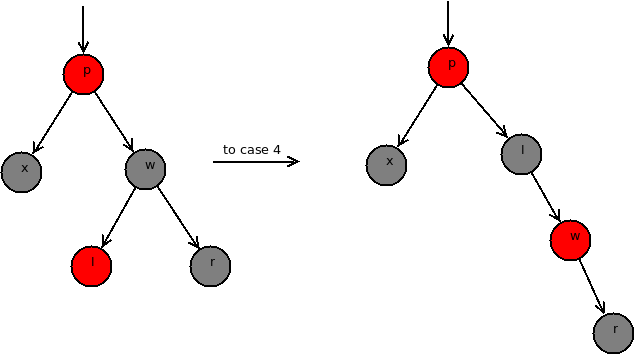
对于情况2，可以先将p节点向左旋转，然后就变为了与情况3一样，如下图所示：

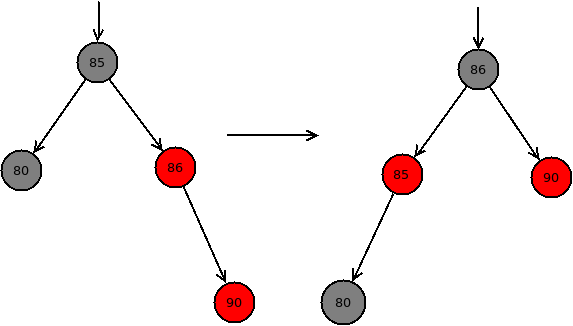
对于情况3，先将节点p设置为黑色，节点q设置为红色，再将节点q向右旋转，这样，p就称为子树的根节点，改变颜色之前，由于p节点为红色，所以q节点一定为黑色，否则原树就不是一棵红黑树，那么将p的颜色改为黑色，q的颜色改为红色，再对q节点进行右旋转，那么p节点就取代了q节点称为子树的根节点，可以看到以p为根节点的子树的黑节点数目没有改变，如下图所示：

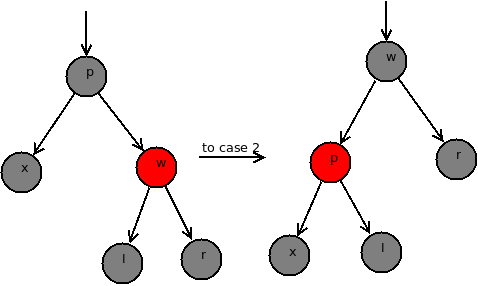
对于情况4，与情况1对称，将z节点的父节点p和叔叔节点y置为黑色，z的祖父间诶点置为红色，如下图所示：

对于情况5，与情况2对称，先将p节点向右旋转，然后就变为与情况6一样，如下图所示：

对于情况6，与情况3对称，先将p节点置为黑色，节点q置为红色，再将q向左旋转，这样p就称为子树的根节点，q称为p的左孩子，如下图所示：

根据上面的分析，红黑树插入代码实现：

红黑树的节点删除

当从红黑树中删除一个节点时，首先按照二叉查找树的删除节点规则进行删除，与二叉查找树不同的是，红黑树中删除一个节点还要改变其子节点的双亲指针。如果删除的是一个红色节点，那么什么都不用做，因为删除红色节点不会破坏红黑树的任何性质，但是如果删除的是一个黑色节点，那么就一定破坏了性质5，也可能破坏性质2和性质4，如果删除的是根节点T，而T的一个红色的孩子称为了新的根节点，那么就会破坏性质2，同理，如果删除的节点y的子节点为红色节点，y的父节点为红色节点，那么会破坏性质4(注意此时删除的节点是指最终从红黑树中移除的节点，这个节点最多只能有一个孩子节点，要么是左孩子，要么是右孩子)。所以在删除节点后还要对这个红黑树进行调整，使这棵树重新满足红黑树的性质。

如果在删除的过程中，红黑树的性质被破坏，可以分为下面的情况来进行调整，假设删除的节点为y，其父节点为p，其兄弟节点为w，删除节点y后，p节点指向y的指针指向x节点：
1. w节点为红色
2. w节点为黑色，w的两个孩子节点都为黑色
3. w节点为黑色，w的右孩子节点为黑色，左孩子节点为红色
4. w节点为黑色，w的右孩子为红色

对于这些情况，又可以分为x为p的左孩子和x为p的右孩子这两种，所以总共有8中情况，下面以x为p的左孩子为例来进行分析，当y节点删除以后，p的左子树上就少了一个黑节点，那么黑节点数目就比p的右子树少1，所以就需要在保持性质2和性质4的基础上对这棵树进行调整，使之满足性质5。

对于情况1，w为红色，那么w的左孩子和右孩子都为黑色节点，w的左子树与右子树根节点到叶节点的路径上的黑节点数目就比x子树上多1，那么将w着色为黑色，将p节点着色为红色，然后将p节点向左旋转处理，w的左孩子l称为p的右孩子，这样l子树路径上的黑色节点个数就比x子树上多1，r子树路径上的黑色节点个数与l子树相同，如下图所示。那么再如何处理呢？其实这样已经转化为了情况2，如情况2的处理，如果l节点的两个孩子都为黑色节点，那么将l节点置为红色，这样l子树路径上就减少一个黑色节点，满足红黑树性质5，但是此时p节点与其右孩子l都为红色节点，破坏性质4，所以此时再将指向x的指针指向p，那么color[x]=RED，那么此时相当于处理的被删除的y节点的孩子节点x为红色节点，可以直接将x节点置为黑色，这样w子树路径上的黑色节点数量增加1，与w右子树路径上的黑色节点数目相同，所以处理完成。

对于情况2，此时将w节点的颜色置为红色，如下图所示。那么p的左右子树上的黑节点数目就相等了，再将p当作x进行重复操作，即将p赋值给x，再进行循环操作，此时x所指向的节点颜色为红色，相当于被删除节点y的子节点为红色，所以直接将当前节点置为黑色即可处理。

对于情况3，将w置为红色，w的左孩子置为黑色，然后对w进行右旋转，就转换成了情况4

对于情况4，由于w为黑色，那么w就为这个多出来的黑节点，那么将p节点置为黑色，将w节点置为红色，然后对p节点进行做旋转，这样，w节点就称为了子树的根节点，并且这棵子树相对于旋转以前多了一个黑节点，右子树相对于旋转以前少了一个黑节点，这样左右子树的黑节点数目相等，如下图所示：

可以看到，在上面四种情况旋转前，相关节点的颜色进行了处理，使之满足性质4，而且这些旋转本质上还是要维持性质5。

如果删除的是根节点，为了满足性质2，在旋转处理的最后设置根节点为黑色。

红黑树与平衡二叉树的区别

红黑树与平衡二叉树都是二叉查找树（二叉排序树）的特殊情况，其实他们都是一种平衡树，相对于二叉查找树，这两种树都不会遇到两个子树中，一个路径较长，而一个路径较短的情况，平衡二叉树相对于红黑树来说更加严格一些，对于查找相较与插入操作较多的情况，平衡二叉树更优一些，因为它是严格平衡的，任何一个节点的左子树与右子树的高度不超过1，如果插入操作较多，那么选择红黑树则更优一些，因为它不会像平衡二叉树旋转的那么频繁。