一、概述
PLONK是最近兴起的零知识证明的一种,在原先零知识证明的基础上进行了优化。我读了网上对于PLONK的解读后,在此进行些许总结。
首先,PLONK的改进主要可分为三个方面:
1、整个方案只设置一个单独的可信设置;
2、多方可参与的可信设置;
3、用多项式承诺代替原先的零知识验证步骤。
二、工作方法
形式是“给我一个值x,我给你一个特定的程序p,这样当x作为输入进行计算时,给出一些具体的结果Y”,类似于zk-snark中的QAP。
首先需要将待求的式子变为电路;
电路上包括两种约束:门约束和复制约束,所谓门约束就是连接到一个门上的线之间的约束,例如输入线为x1,x2,进入乘法门,输出y,则门约束就是x1*x2=y;
复制约束是电路中任何位置的不同线相等的声明。
三、具体内容
1、将线性系统表示为多项式:(门约束)
L(x)*x1+M(x)*x2+R(x)*x3-O(x)=Z(x)H(x)
因为上述式子中的x1,x2,x3是变量,在每个方程中不同,为乐实现统一化,需要将变量本身成为多项式而不是常数来处理这个问题。
2、复制约束
复制约束的实现依赖了一个名为“坐标对累加器的方法”
举例:
一个多项式p(x) 的工作原理如下:首先,让X(x)和Y(x)两个多项式表示一组点的x和y坐标(例如表示集合((0, -2), (1, 1), (2, 0), (3, 1)), 你可设置X(x) = x以及Y(x) = x^3 - 5x^2 + 7x - 2)。我们的目标是让p(x) 代表所有点,直到(但不包括)给定的位置,所以 p(0)从1开始,p(1)只代表第一个点,p(2)是第一个点和第二个点,诸如此类。我们将通过“随机”选择两个常数v1和v2,并使用约束p(0) = 1以及p(x+1) = p(x) * (v1 + X(x) + v2 * Y(x)) 构造p(x),至少在域(0,1,2,3)内。例如,让v1=3和v2=2,我们得到:

我们关心的结果是p(4) = -240 。现在,考虑这样的情况,我们设置X(x) = 2⁄3 x^3 - 4x^2 + 19⁄3 x(即,在坐标(0,1,2,3)处定值为(0,3,2,1)的多项式) ,而不是X(x) = x。
如果你运行同样的过程,你会发现你也会得到p(4) = -240。
这不是巧合(事实上,如果你随机从一个足够大的域中选择v1和v2,则几乎永远不会巧合地发生)。相反,这是因为 Y(1) = Y(3),所以如果你“交换”点 (1, 1) 和(3,1)的X坐标,你就不会改变点的集合,并且因为累加器对集合进行编码(因为乘法不关心顺序),所以最后的值将是相同的。
小结:简单来说当y的值相同时,任意改变x的值,最后的结果不变。当需要证明a,b,c之间的约束时,则不像之前检查一次中的相等性(即检查p(4) = p’(4)),而是检查每侧三次不同运行的乘积:

阶段综述:
第一步首先检查门约束:
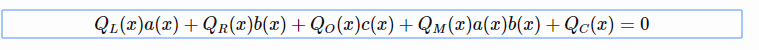
第二步检查复制约束:
然后多项式累加器开始和结束约束:
所以现在我们已经把程序满足问题,变成了用多项式满足几个方程的简单问题,PLONK中有一些优化,其可以允许我们去掉上面方程中的很多多项式,为了简单考虑,我将不再讨论这些。但是多项式本身(无论是程序特定的参数还是用户输入),都是很大的。
所以下一个问题是,我们如何绕过这个问题,才能让证明变简短?
3、多项式承诺
commitment一般分为commit和reveal两个阶段,commit整个过程可形象描述为a committer P将某个信息m放进了一个密码箱中,箱子上锁后归a verifier V所有,锁钥匙归P所有;reveal过程为P将钥匙给V,V打开箱子可查看里面的信息m。commitment具有如下特性:
hiding特性:即V拥有了上锁的箱子,由于没有钥匙无法获取里面的信息m。
binding特性:即尽管P拥有了钥匙,但是箱子归V所有,P无法在上锁后再次开锁修改其中的信息为m’。即某个值commit后,将不可修改。
多项式承诺(polynomial commitment)是一个短对象,其“代表”一个多项式,并允许你验证该多项式的计算,而不需要实际包含多项式中的所有数据。也就是说,如果有人给你一个代表P(x)的承诺c,他们可以给你一个证明,然后说服你对于某个特定的z,P(z) 值是多少。还有一个进一步的数学结果表明,在一个足够大的域上,如果关于在随机z上定值的多项式的某些类型的方程(在z已知之前选择)是真的,那么这些相同的方程对整个多项式也是真的。例如,如果P(z) * Q(z) + R(z) = S(z) + 5,那么我们知道P(x) * Q(x) + R(x) = S(x) + 5通常是极有可能的。使用这样的多项式承诺,我们可以很容易地检查上面所有的多项式方程。作出承诺,使用它们作为输入生成z,证明在z上每个多项式的定值是什么,然后用这些定值来运行方程,而不是原来的多项式。(将多项式转化为了定值,从而更简单)
另请注意一个一般优化:为了同时证明多个多项式的多个opening,在提交输出后,对多项式和输出的随机线性组合执行减除技巧。
那么,承诺本身是如何运作的呢?幸运的是,Kate 承诺要比FRI简单得多。可信设置过程生成一组椭圆曲线点G, G * s, G * s^2 …. G * s^n,以及G2 * s,其中G 和G2是两个椭圆曲线组的生成器,而s则是一个一旦程序完成就会被遗忘的秘密(注意,这个设置有多个版本,它是安全的,只要至少有一个参与者忘记了他们分享的秘密)。这些点会被公布,并被认为是方案的“证明关键”,任何需要作出多项式承诺的人都需要使用这些点。通过将证明密钥中的前d+1个点中的每一点乘以多项式中的相应系数,并将结果相加,对d次多项式作出承诺。
注意,这提供了在s处的多项式的“定值”,而不知道s。例如,x^3 + 2x^2+5 将由(G * s^3) + 2 * (G * s^2) + 5 * G表示。我们可以用符号[P]来表示用这种方式(即G * P(s))编码的P。在做减除技巧时,可以使用椭圆曲线对来证明这两个多项式实际上满足关系:检查e([P] - G * a, G2) = e([Q], [x] - G2 * z)是否作为检查P(x) - a = Q(x) * (x - z)的代理。
四、总结
最后,我们再讨论一下这个方案,给定一个程序P,将其转换为一个电路,并生成一组如下所示的方程:
然后将这组方程转换为一个多项式方程:
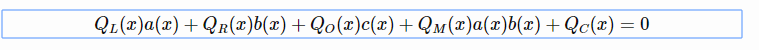
你还可以从回路中生成复制约束的列表。从这些复制约束生成表示排列线指数的三个多项式:σa(x), σb(x), σc(x)。要生成证明,需要计算所有线的值,并将其转换为三个多项式:a(x), b(x), c(x)。作为置换检查参数的一部分,你还可以计算六个“坐标对累加器”多项式。最后计算辅因子Hi(x)。
多项式之间有一组方程需要检查,你可以通过对多项式作出承诺,在某些随机z处打开它们(同时证明这些opening是正确的),并在这些求值结果上运行方程,而不是在原始多项式上运行方程来完成这项工作。证明本身只是一些承诺和opening,可以用几个方程式来检查。








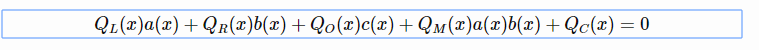
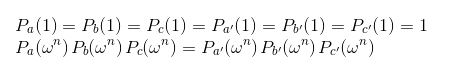
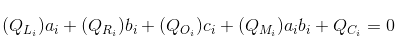













 1629
1629











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








