文章源码在Github:https://github.com/jinchenghao/TSP
本介绍用python解决TSP问题的第二个方法——动态规划法
算法介绍
动态规划算法根据的原理是,可以将原问题细分为规模更小的子问题,并且原问题的最优解中包含了子问题的最优解。也就是说,动态规划是一种将问题实例分解为更小的、相似的子问题,并存储子问题的解而避免计算重复的子问题,以解决最优化问题的算法策略。
我使用DP求解TSP问题的主要分为三个主要部分:
1) 假定我们从城市0出发,经过了所有城市,并返回到城市0。那么我们需要记录的信息有:当前所在城市location,当前未遍历的城市集合s。
2) 状态转移方程,状态转移方程是DP算法的核心部分,它代表了子问题和原问题的关系,通过状态转移方程可以将原问题不断细分为各个子问题。我们状态转移方程的定义如下所示:
T(s,init)代表的意思是从init点出发经过s中全部的点回到init的距离。
3) 构建T表记录T的值,如果不去记录每次递归的T值,那么以后每次搜索都要重新计算,就成了暴力搜索。所以我们构建一个T表dp[s][init],记录每次求出来的T函数值,即将T(s,init)的值记录在dp[s][init]位置。
程序
输入:
1 2066 2333
2 935 1304
3 1270 200
4 1389 700
5 984 2810
6 2253 478
7 949 3025
8 87 2483
9 3094 1883
10 2706 3130代码:
"""
动态规划法
name:xxx
date:6.8
"""
import pandas as pd
import numpy as np
import math
import time
dataframe = pd.read_csv("./data/TSP10cities.tsp",sep=" ",header=None)
v = dataframe.iloc[:,1:3]
train_v= np.array(v)
train_d=train_v
dist = np.zeros((train_v.shape[0],train_d.shape[0]))
#计算距离矩阵
for i in range(train_v.shape[0]):
for j in range(train_d.shape[0]):
dist[i,j] = math.sqrt(np.sum((train_v[i,:]-train_d[j,:])**2))
"""
N:城市数
s:二进制表示,遍历过得城市对应位为1,未遍历为0
dp:动态规划的距离数组
dist:城市间距离矩阵
sumpath:目前的最小路径总长度
Dtemp:当前最小距离
path:记录下一个应该到达的城市
"""
N=train_v.shape[0]
path = np.ones((2**(N+1),N))
dp = np.ones((2**(train_v.shape[0]+1),train_d.shape[0]))*-1
def TSP(s,init,num):
if dp[s][init] !=-1 :
return dp[s][init]
if s==(1<<(N)):
return dist[0][init]
sumpath=1000000000
for i in range(N):
if s&(1<<i):
m=TSP(s&(~(1<<i)),i,num+1)+dist[i][init]
if m<sumpath:
sumpath=m
path[s][init]=i
dp[s][init]=sumpath
return dp[s][init]
if __name__ == "__main__":
init_point=0
s=0
for i in range(1,N+1):
s=s|(1<<i)
start = time.clock()
distance=TSP(s,init_point,0)
end = time.clock()
s=0b11111111110
init=0
num=0
print(distance)
while True:
print(path[s][init])
init=int(path[s][init])
s=s&(~(1<<init))
num+=1
if num>9:
break
print("程序的运行时间是:%s"%(end-start))
结果:








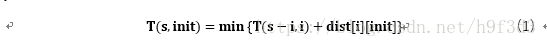














 5281
5281











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








