时间复杂度和空间复杂度

时间复杂度和空间复杂度是衡量一个算法复杂度的重要依据，所以它对我们分析算法和写代码很重要

时间复杂度：语句总的执行次数与问题规模n的函数表达式

一般算法时间复杂度的计算方法：

• 用常数1取代运行时间中所有的加法常数
• 在修改后的运行次数函数中，只保留最高阶
• 如果最高阶项系数存在而且不是1，则去除与这个项相乘的常数，把它变为1

空间复杂度：函数中创建对象的个数关于问题的规模函数表达式

一般算法时间复杂度的计算方法：创建变量的个数

区别：时间是累积的，但是空间不是累积的，可重复使用。

分治算法的时间复杂度

最常见的是折半查找，既二分查找的时间复杂度。如果有N个数，把这个序列转换为一颗二叉搜索树，既这棵树有N个结点，它查找一个结点需要比较那个结点所在的深度次。最大比较次数为树的深度，既㏒₂N，所以它的时间复杂度为O（㏒₂N），我们经常把它简写成O（㏒N）。

递归算法的时间复杂度和空间复杂度

• 时间复杂度=递归的总次数*每次递归函数里边执行的系数
• 空间复杂度：递归的深度*每次栈帧的个数

分析斐波那契数列的时间复杂度和空间复杂度

• 递归

int fib(size_t n)
{
    return n < 2 ? n : fib(n - 1) + fib(n - 2);
}

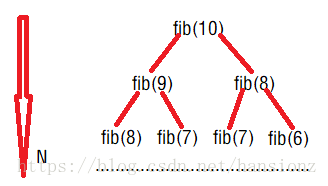
分析：从上图可以看出斐波那契数列递归做法是一个二叉树，递归的总次数为二叉树的结点个数2^n-1个。则时间复杂度为O(2^n)。空间复杂度为递归的深度*每次递归的栈帧数，既为O(n)

• 非递归：从上图可以看出对于斐波那契数列递归的做法效率实在太低了，因为重复计算的值非常的多，所以我们可以考虑非递归算法

long long fib(size_t n)
{
    int n1 = 0, n2 = 1, n3 = n;
    int i = 2;
    //这里一定是<=否则会少计算一个
    for (; i <= n; i++)
    {
        n3 = n2 + n1;
        n1 = n2;
        n2 = n3;
    }
    return n3;
}

很容易计算出非递归算法的时间复杂度为O(n)，空间复杂度为O(1)。