1 树的基本概念
- 节点、根节点、父节点、子节点、兄弟节点
- 空树:一棵树可以没有任何节点
- 一棵树可以只有 1 个节点,这个节点其实就是根节点
- 子树、左子树、右子树
- 节点的度:子树的个数
- 树的度:所有节点度中的最大值
- 叶子节点:度为 0 的节点
- 非叶子节点:度不为 0 的节点
- 层数(level):根节点在第 1 层,根节点的子节点在第 2 层,以此类推(有些教程也从第 0 层开始计算)
- 节点的深度(depth):从根节点到当前节点的唯一路径上的节点总数,即从上往下数
- 节点的高度(height):从当前节点到最远叶子节点的路径上的节点总数,即从下往上数
- 树的深度:所有节点深度中的最大值
- 树的高度:所有节点高度中的最大值
- 树的深度=树的高度
- 有序树:树中任意节点的子节点之间有顺序关系
- 无序树、自由树:树中任意节点的子节点之间没有顺序关系
- 森林:由m(m ≥ 0)棵互不相交的树组成的集合
2 二叉树(Binary Tree)
- 每个节点的度最大为2(最多拥有 2 棵子树)
- 左子树和右子树是有顺序的
- 即使某节点只有一棵子树,也要区分左右子树
2.1 二叉树性质
- 非空二叉树的第 i 层,最多有2^(i − 1)个节点( i ≥ 1 )
- 在高度为 h 的二叉树上最多有 2^h − 1 个结点(h ≥ 1 )
- 对于任何一棵非空二叉树,如果叶子节点个数为 n0,度为 2 的节点个数为 n2,则有: n0 = n2 + 1
- 二叉树节点总数n = n0+n1+n2
- 度为1的节点有两条边,而度为2的节点有一条边,所以总边数 = n1+2*n2
- 除了根节点外,每个节点头上,都有一个边,所以总边数 = n-1
- 综上推断出n0 = n2+1
2.2 真二叉树(Proper Binary Tree)
所有节点的度都要么为 0,要么为 2
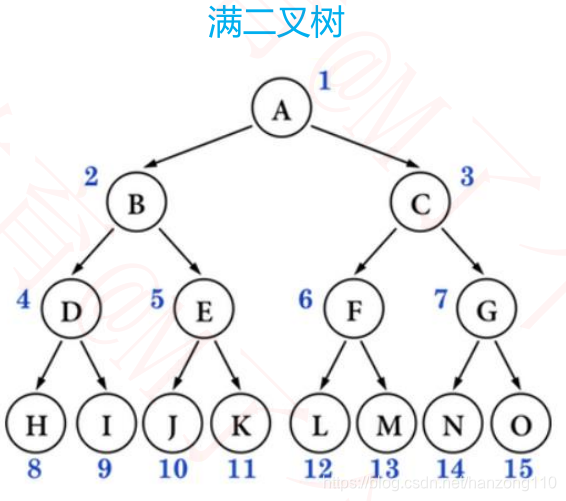
2.3 满二叉树(Full Binary Tree)
- 最后一层节点的度都为 0,其他节点的度都为 2
- 高度h = log2(n + 1)
- 总节点数n = 2^h − 1 = 2 ^ 0 + 2 ^1 + 2 ^2 + ⋯+ 2 ^(h−1)
2.4 完全二叉树(Complete Binary Tree)
- 对节点从上至下、左至右开始编号,其所有编号都能与相同高度的满二叉树中的编号对应
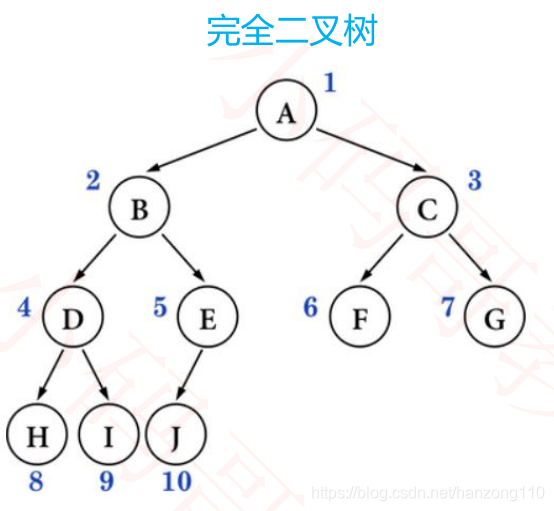
- 假设完全二叉树的高度为 h( h ≥ 1 ),那么
- 至少2^(h − 1) 个节点 ( 2 ^0 + 2 ^1 + 2 ^2 + ⋯+ 2 ^h)
- 最多有2^h-1个节点
- 因此高度h = floor(log2(n))+1,floor为向下取整、ceiling为向上取整
- 从上到下、从左到右对节点从 0 开始进行编号,对任意第 i 个节点
- 如果 i = 0 ,它是根节点
- 如果 i > 0 ,它的父节点编号为 floor( (i-1) / 2 )
- 如果 2i+1 ≤ n-1 ,它的左子节点编号为 2i+1,如果 2i+1 > n-1 ,它无左子节点
- 如果 2i + 2 ≤ n -1,它的右子节点编号为 2i + 2,如果 2i + 2 > n-1 ,它无右子节点
- 度为1的节点要么是1个,要么是0个
- 叶子节点个数n0 = floor((n+1)/2)
- 非叶子节点个数n1+n2 = floor(n/2)
2.5 二叉树的遍历
- 前序遍历(Preorder Traversal):根节点、前序遍历左子树、前序遍历右子树,适用于树状结构展示(注意左右子树的顺序)
- 通过观察,访问过程中,可以先拿到5,再拿到3的,但真正访问,确实先访问3再访问5,所以考虑使用栈来实现
- 使用栈实现
- 先访问根节点
- 将当前访问的节点的右节点入栈
- 继续访问左节点,如果左节点为null,说明左子树访问完毕,应开始访问右子树,因此出栈一个节点,作为新的节点
- 循环执行直到左节点为null,并且栈中也没有元素时结束
- 使用递归实现
//使用栈实现
public void preorder2(Visitor<E> visitor) {
if (visitor == null || root == null) return;
Node<E> node = root;
Stack<Node<E>> stack = new Stack<>();
while (true) {
if (node != null) {
// 访问node节点
if (visitor.visit(node.element)) return;
// 将右子节点入栈
if (node.right != null) {
stack.push(node.right);
}
// 向左走
node = node.left;
} else if (stack.isEmpty()) {
return;
} else {
// 处理右边
node = stack.pop();
}
}
}
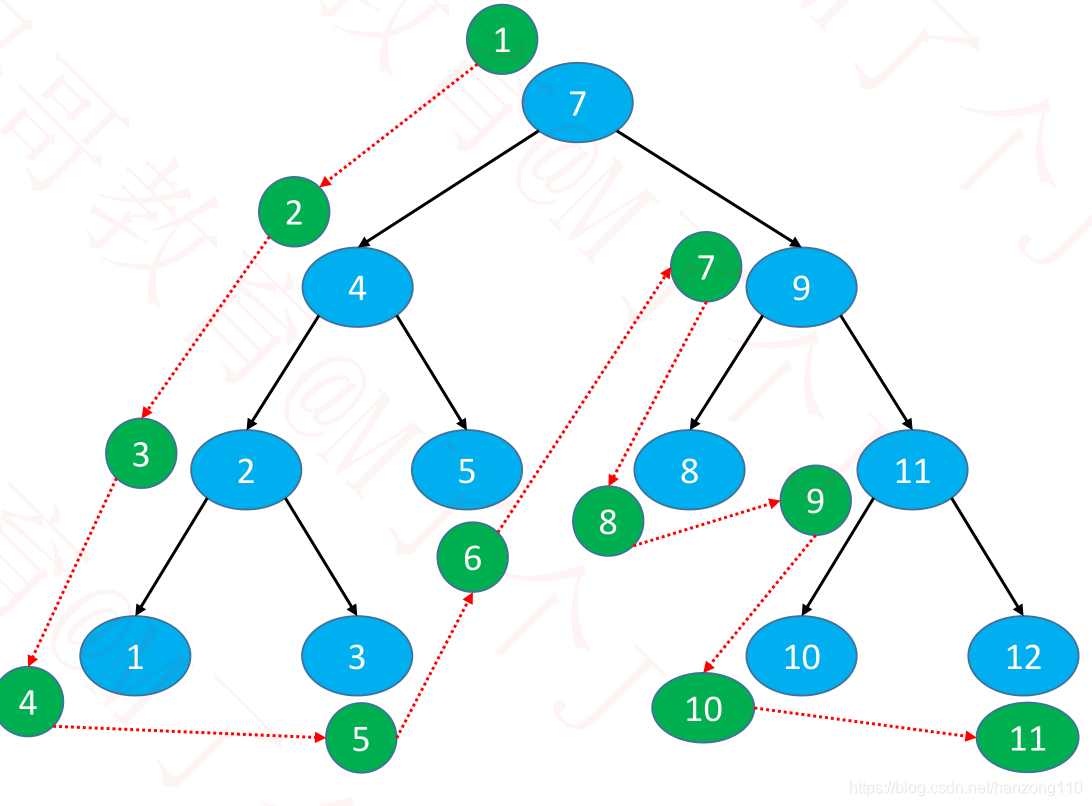
- 中序遍历(Inorder Traversal):中序遍历左子树、根节点、中序遍历右子树,适用于二叉搜索树的中序遍历按升序或者降序处理节点
- 通过观察,访问过程中,可以先拿到4,再拿到2的,但真正访问,确实先访问2再访问4,所以考虑使用栈来实现
- 使用栈实现
- 先入栈,再向左走
- 直到左边没有节点,出栈,访问,如果有节点存在,对其中序遍历,如果不存在继续出栈,直到栈中元素为空
//使用栈实现
public void inorder(Visitor<E> visitor) {
if (visitor == null || root == null) return;
Node<E> node = root;
Stack<Node<E>> stack = new Stack<>();
while (true) {
if (node != null) {
stack.push(node);
// 向左走
node = node.left;
} else if (stack.isEmpty()) {
return;
} else {
node = stack.pop();
// 访问node节点
if (visitor.visit(node.element)) return;
// 让右节点进行中序遍历
node = node.right;
}
}
}
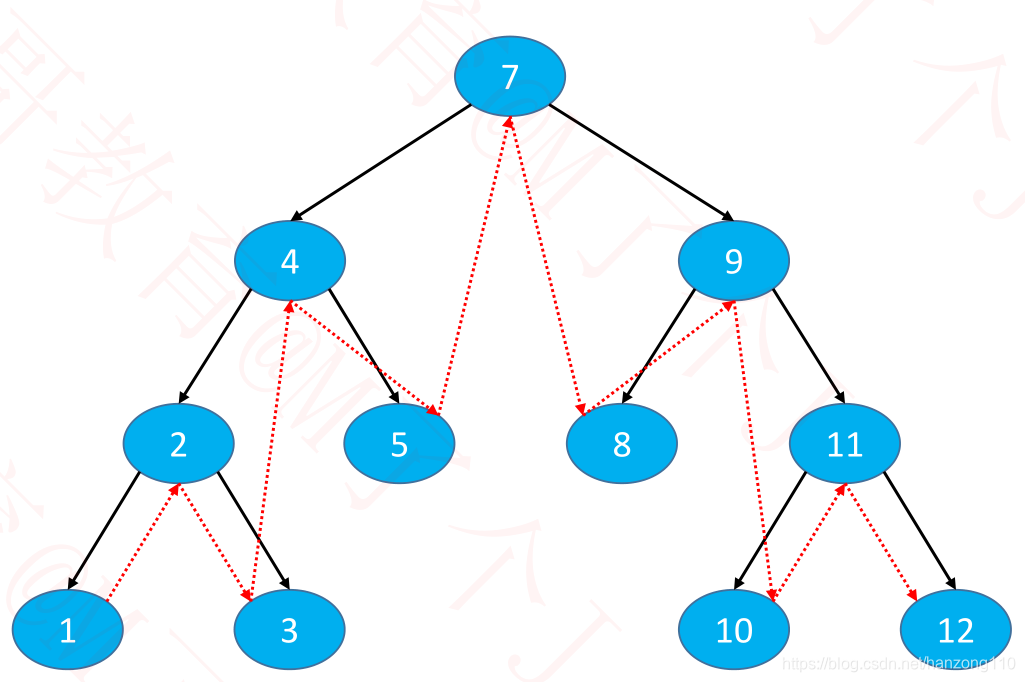
4. 后序遍历(Postorder Traversal):后序遍历左子树、后序遍历右子树、根节点,适用于一些先子后父的操作
1. 使用栈实现:
1. 将根节点入栈
2. 循环执行以下操作,直到栈为空
1. 如果栈顶节点为叶子节点(1),或者上一次访问的节点是栈顶节点的子节点(先访问了3后访问2)
2. 弹出栈顶节点,进行访问
3. 否则 将栈顶节点的right、left按顺序入栈
public void postorder(Visitor<E> visitor) {
if (visitor == null || root == null) return;
// 记录上一次弹出访问的节点
Node<E> prev = null;
Stack<Node<E>> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node<E> top = stack.peek();
if (top.isLeaf() || (prev != null && prev.parent == top)) {
prev = stack.pop();
// 访问节点
if (visitor.visit(prev.element)) return;
} else {
if (top.right != null) {
stack.push(top.right);
}
if (top.left != null) {
stack.push(top.left);
}
}
}
}
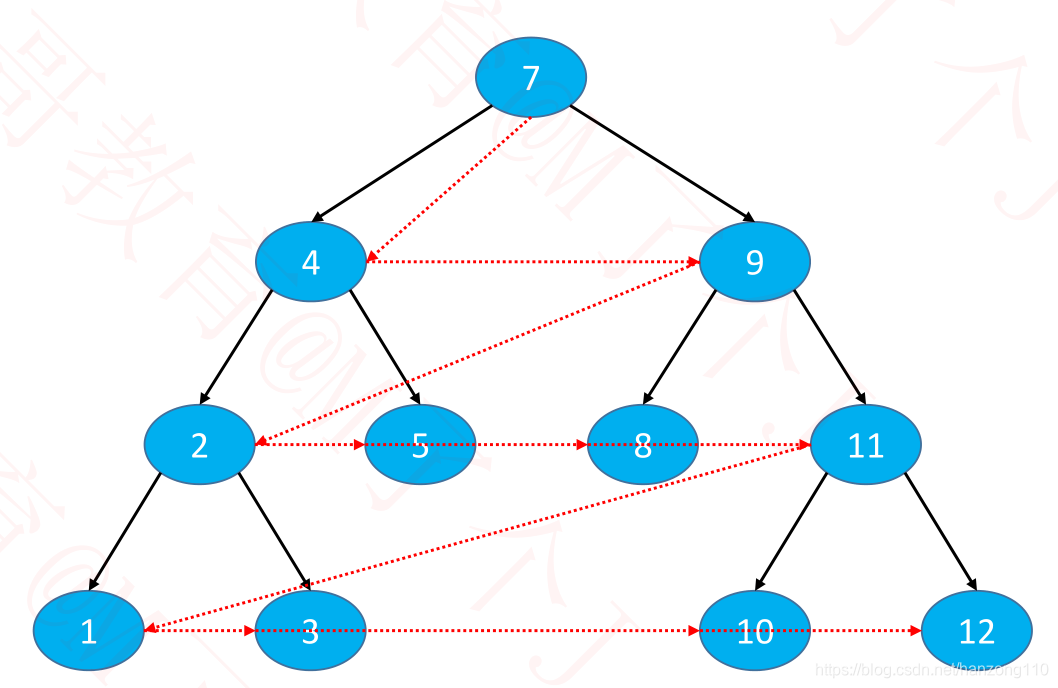
5. 层序遍历(Level Order Traversal):从上到下、从左到右依次访问每一个节点
1. 使用队列
1. 根节点入队
2. 根节点出队、左子节点入队、右子节点入队
3. 左子节点X出队,X的左子节点入队、右子节点入队
2. 适用于
1. 计算二叉树的高度
2. 判断一棵树是否为完全二叉树
3 前驱节点与后继节点
3.1 前驱节点
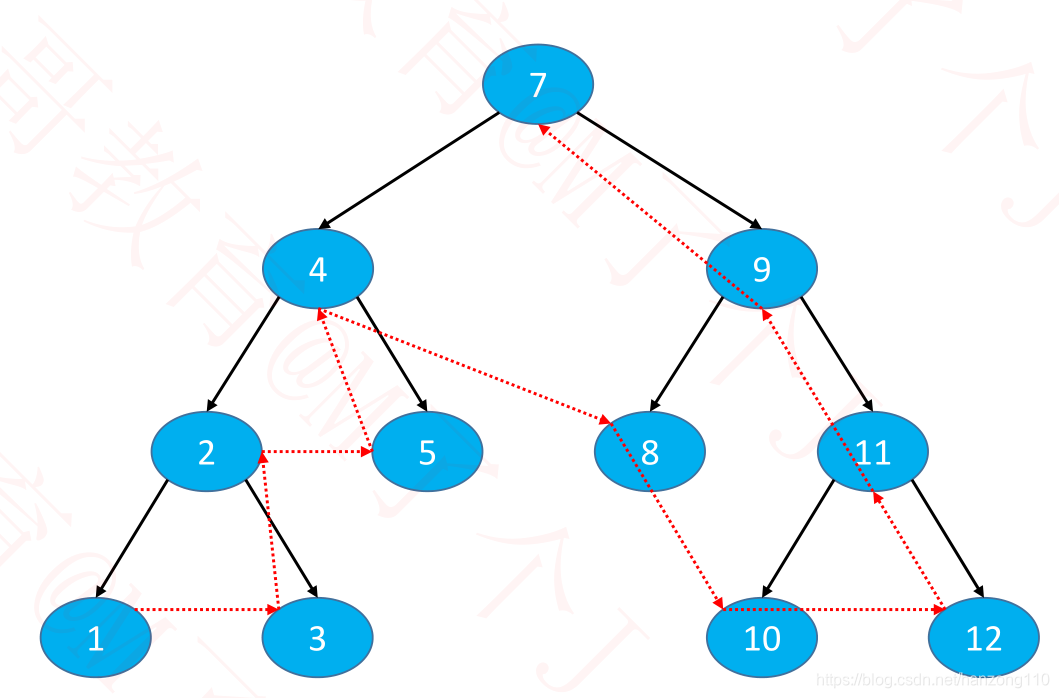
- 中序遍历时的前一个节点
- 如果是二叉搜索树,前驱节点就是前一个比它小的节点
- 获取前驱节点时,分为三种情况
- node.left != null:例如6、13、8
- predecessor = node.left.right.right.right…,直到right为null
- node.left = null && node.parent != null:例如7、11、9、1
- predecessor = node.parent.parent.parent…,直到node在parent的右子树中
- nodeleft = null && node.parent = null:例如没有左子树的根节点
- 没有前驱节点
- node.left != null:例如6、13、8
3.2 后继节点
与前驱节点完全相反
4 二叉搜索树
4.1 产生原因
- 在 n 个动态的整数中搜索某个整数,假设使用动态数组存放元素,从第 0 个位置开始遍历搜索,平均时间复杂度:O(n)
- 如果维护一个有序的动态数组,使用二分搜索,最坏时间复杂度:O(logn),但是添加、删除的平均时间复杂度是 O(n)
- 因此产生二叉搜索树,添加、删除、搜索的最坏时间复杂度均可优化至:O(logn)
4.2 性质
- 二叉搜索树是二叉树的一种,是应用非常广泛的一种二叉树,英文简称为 BST
- 又被称为:二叉查找树、二叉排序树
- 任意一个节点的值都大于其左子树所有节点的值
- 任意一个节点的值都小于其右子树所有节点的值
- 二叉搜索树存储的元素必须具备可比较性,如果是自定义类型,需要指定比较方式
4.3 成员变量
- element:存放具体元素
- parent:存放指向父节点的指针
- left:指向左子节点
- right:指向右子节点
4.4 添加方法
- 找到父节点
- 使用父节点来创建新节点
- parent.left = node 或者 parent.right = node
- 遇到相等的元素,可以考虑用新值覆盖旧值
4.5 元素间比较方案
- 允许外界传入一个 Comparator 自定义比较方案
- 如果没有传入 Comparator,强制认定元素实现了 Comparable 接口
4.6 打印二叉树
- 网站
https://github.com/CoderMJLee/BinaryTrees
- 使用方法
- 自定义的二叉树实现BinaryTreeInfo接口
- 重写该接口中root、left、right、string接口
- 客户端代码中可以通过BinaryTrees.println(bst);进行打印
4.7 删除节点
- 要删除的节点为叶子节点:直接删除
- 判断该节点是其父节点的左子节点还是右子节点
- 如果是右子节点:node.parent.right = null
- 如果是左子节点:node.parent.left = null
- 如果压根没有父节点,说明正在删除根节点:root = null
- 删除度为1的节点:用该节点的子节点替代该节点
- 如果其子节点在右侧:node.parent.left = child
- 如果其子节点在左侧: node.parent.right = child
- 如果父节点为空,表示为根节点:root = child
- 删除度为2 的节点:用该节点的前驱节点或后继节点覆盖该节点,然后删除前驱、后继节点
- 如果一个节点的度为2,其前驱节点或后继节点的度只可能是1或0
4.8 代码
- BinaryTree
package com.mj.tree;
import java.util.LinkedList;
import java.util.Queue;
import com.mj.printer.BinaryTreeInfo;
@SuppressWarnings("unchecked")
public class BinaryTree<E> implements BinaryTreeInfo {
protected int size;
protected Node<E> root;
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public void clear() {
root = null;
size = 0;
}
public void preorder(Visitor<E> visitor) {
if (visitor == null) return;
preorder(root, visitor);
}
private void preorder(Node<E> node, Visitor<E> visitor) {
if (node == null || visitor.stop) return;
visitor.stop = visitor.visit(node.element);
preorder(node.left, visitor);
preorder(node.right, visitor);
}
public void inorder(Visitor<E> visitor) {
if (visitor == null) return;
inorder(root, visitor);
}
private void inorder(Node<E> node, Visitor<E> visitor) {
if (node == null || visitor.stop) return;
inorder(node.left, visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
inorder(node.right, visitor);
}
public void postorder(Visitor<E> visitor) {
if (visitor == null) return;
postorder(root, visitor);
}
private void postorder(Node<E> node, Visitor<E> visitor) {
if (node == null || visitor.stop) return;
postorder(node.left, visitor);
postorder(node.right, visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
}
public void levelOrder(Visitor<E> visitor) {
if (root == null || visitor == null) return;
Queue<Node<E>> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
if (visitor.visit(node.element)) return;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
public boolean isComplete() {
if (root == null) return false;
Queue<Node<E>> queue = new LinkedList<>();
queue.offer(root);
boolean leaf = false;
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
if (leaf && !node.isLeaf()) return false;
if (node.left != null) {
queue.offer(node.left);
} else if (node.right != null) {
return false;
}
if (node.right != null) {
queue.offer(node.right);
} else { // 后面遍历的节点都必须是叶子节点
leaf = true;
}
}
return true;
}
public int height() {
if (root == null) return 0;
// 树的高度
int height = 0;
// 存储着每一层的元素数量
int levelSize = 1;
Queue<Node<E>> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
levelSize--;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
if (levelSize == 0) { // 意味着即将要访问下一层
levelSize = queue.size();
height++;
}
}
return height;
}
public int height2() {
return height(root);
}
private int height(Node<E> node) {
if (node == null) return 0;
return 1 + Math.max(height(node.left), height(node.right));
}
protected Node<E> createNode(E element, Node<E> parent) {
return new Node<>(element, parent);
}
protected Node<E> predecessor(Node<E> node) {
if (node == null) return null;
// 前驱节点在左子树当中(left.right.right.right....)
Node<E> p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
// 从父节点、祖父节点中寻找前驱节点
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
// node.parent == null
// node == node.parent.right
return node.parent;
}
protected Node<E> successor(Node<E> node) {
if (node == null) return null;
// 前驱节点在左子树当中(right.left.left.left....)
Node<E> p = node.right;
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
// 从父节点、祖父节点中寻找前驱节点
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
return node.parent;
}
public static abstract class Visitor<E> {
boolean stop;
/**
* @return 如果返回true,就代表停止遍历
*/
abstract boolean visit(E element);
}
protected static class Node<E> {
E element;
Node<E> left;
Node<E> right;
Node<E> parent;
public Node(E element, Node<E> parent) {
this.element = element;
this.parent = parent;
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
public boolean isLeftChild() {
return parent != null && this == parent.left;
}
public boolean isRightChild() {
return parent != null && this == parent.right;
}
public Node<E> sibling() {
if (isLeftChild()) {
return parent.right;
}
if (isRightChild()) {
return parent.left;
}
return null;
}
}
@Override
public Object root() {
return root;
}
@Override
public Object left(Object node) {
return ((Node<E>)node).left;
}
@Override
public Object right(Object node) {
return ((Node<E>)node).right;
}
@Override
public Object string(Object node) {
return node;
}
}
- BST
package com.mj.tree;
import java.util.Comparator;
@SuppressWarnings("unchecked")
public class BST<E> extends BinaryTree<E> {
private Comparator<E> comparator;
public BST() {
this(null);
}
public BST(Comparator<E> comparator) {
this.comparator = comparator;
}
public void add(E element) {
elementNotNullCheck(element);
// 添加第一个节点
if (root == null) {
root = createNode(element, null);
size++;
// 新添加节点之后的处理
afterAdd(root);
return;
}
// 添加的不是第一个节点
// 找到父节点
Node<E> parent = root;
Node<E> node = root;
int cmp = 0;
do {
cmp = compare(element, node.element);
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else { // 相等
node.element = element;
return;
}
} while (node != null);
// 看看插入到父节点的哪个位置
Node<E> newNode = createNode(element, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
// 新添加节点之后的处理
afterAdd(newNode);
}
/**
* 添加node之后的调整
* @param node 新添加的节点
*/
protected void afterAdd(Node<E> node) { }
/**
* 删除node之后的调整
* @param node 被删除的节点
*/
protected void afterRemove(Node<E> node) { }
public void remove(E element) {
remove(node(element));
}
public boolean contains(E element) {
return node(element) != null;
}
private void remove(Node<E> node) {
if (node == null) return;
size--;
if (node.hasTwoChildren()) { // 度为2的节点
// 找到后继节点
Node<E> s = successor(node);
// 用后继节点的值覆盖度为2的节点的值
node.element = s.element;
// 删除后继节点
node = s;
}
// 删除node节点(node的度必然是1或者0)
Node<E> replacement = node.left != null ? node.left : node.right;
if (replacement != null) { // node是度为1的节点
// 更改parent
replacement.parent = node.parent;
// 更改parent的left、right的指向
if (node.parent == null) { // node是度为1的节点并且是根节点
root = replacement;
} else if (node == node.parent.left) {
node.parent.left = replacement;
} else { // node == node.parent.right
node.parent.right = replacement;
}
// 删除节点之后的处理
afterRemove(node);
} else if (node.parent == null) { // node是叶子节点并且是根节点
root = null;
// 删除节点之后的处理
afterRemove(node);
} else { // node是叶子节点,但不是根节点
if (node == node.parent.left) {
node.parent.left = null;
} else { // node == node.parent.right
node.parent.right = null;
}
// 删除节点之后的处理
afterRemove(node);
}
}
private Node<E> node(E element) {
Node<E> node = root;
while (node != null) {
int cmp = compare(element, node.element);
if (cmp == 0) return node;
if (cmp > 0) {
node = node.right;
} else { // cmp < 0
node = node.left;
}
}
return null;
}
/**
* @return 返回值等于0,代表e1和e2相等;返回值大于0,代表e1大于e2;返回值小于于0,代表e1小于e2
*/
private int compare(E e1, E e2) {
if (comparator != null) {
return comparator.compare(e1, e2);
}
return ((Comparable<E>)e1).compareTo(e2);
}
private void elementNotNullCheck(E element) {
if (element == null) {
throw new IllegalArgumentException("element must not be null");
}
}
}
5 平衡二叉搜索树(Balanced Binary Search Tree)BBST
- 当节点数量固定时,左右子树的高度越接近,这棵二叉树就越平衡(高度越低)
- 最理想的平衡,就是像完全二叉树、满二叉树那样,高度是最小的
- 改进二叉搜索树:在节点的添加、删除操作之后,想办法让二叉搜索树恢复平衡(减小树的高度)
- 比较合理的改进方案是:用尽量少的调整次数达到适度平衡即可
- 一棵达到适度平衡的二叉搜索树,可以称之为:平衡二叉搜索树
- 经典常见的平衡二叉搜索树有
- AVL树
- 红黑树
- 他们一般也称为自平衡的二叉搜索树(Self-balancing Binary Search Tree)
6 AVL树
- 平衡因子(Balance Factor):也就是使其平衡的因素,为某结点的左右子树的高度差
- AVL树特点:每个节点的平衡因子只可能是 1、0、-1(绝对值 ≤ 1,如果超过 1,称之为“失衡”)
- AVL树的AVLNode多了一个表示高度的height,默认高度为1
6.1 添加导致的失衡处理
- 在添加方法最后,增加一个afterAdd方法,用于更新高度变化了的节点的高度,并回复平衡
- 可以想象,添加会导致其父节点和祖先节点高度变化,因此添加不会导致父节点和非祖先节点失衡
- 只要回复第一个不平衡的节点,所有的不平衡节点就都恢复平衡
- 循环找新增加节点的父节点
- 如果平衡,更新该节点高度(左右子节点中最高的高度+1)
- 如果不平衡,恢复平衡,并退出循环
- 根据第一个不平衡的节点grand、其最高的子节点parent、parent最高的子节点node的位置情况,将不平衡分为四种不同
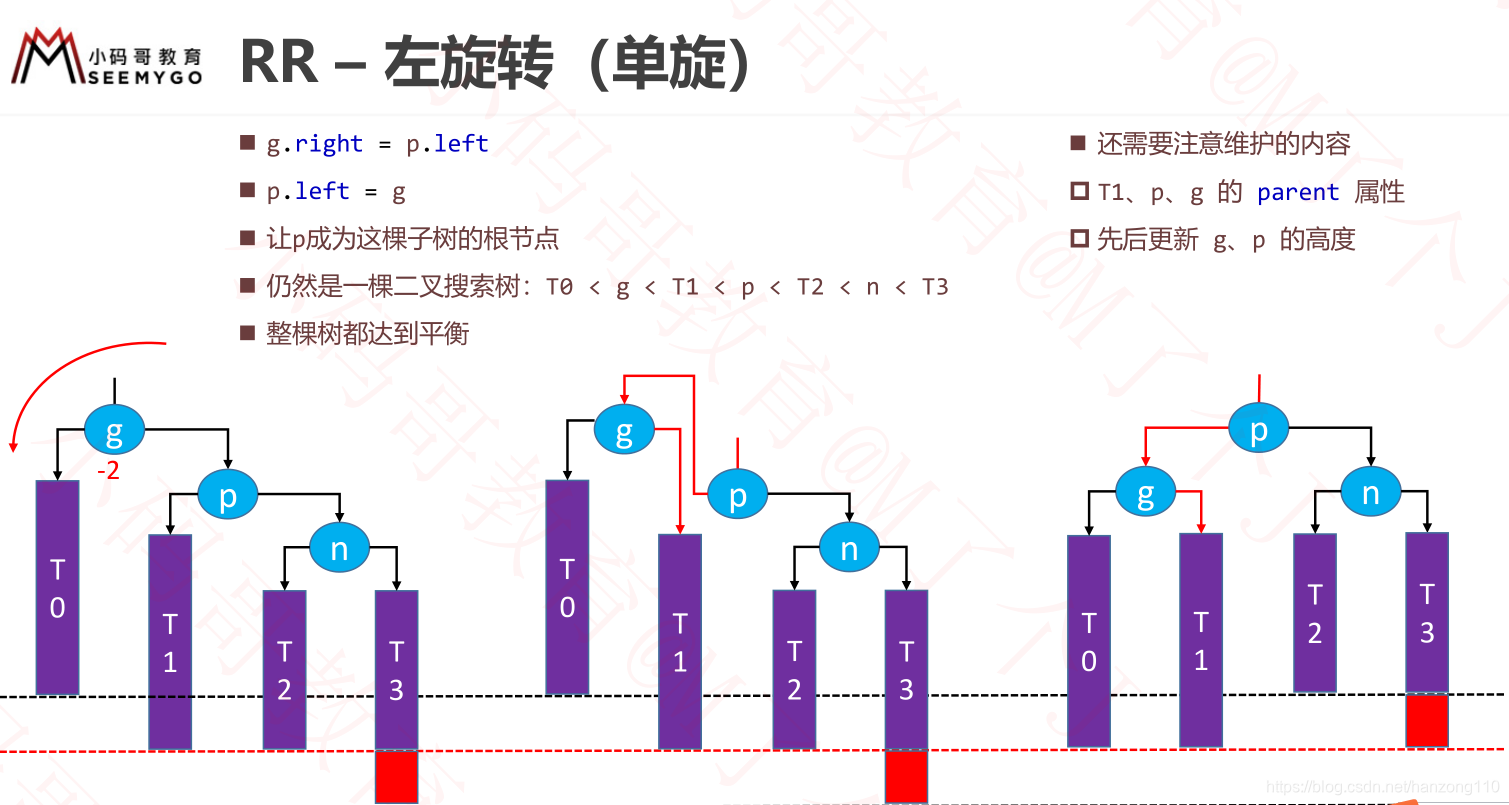
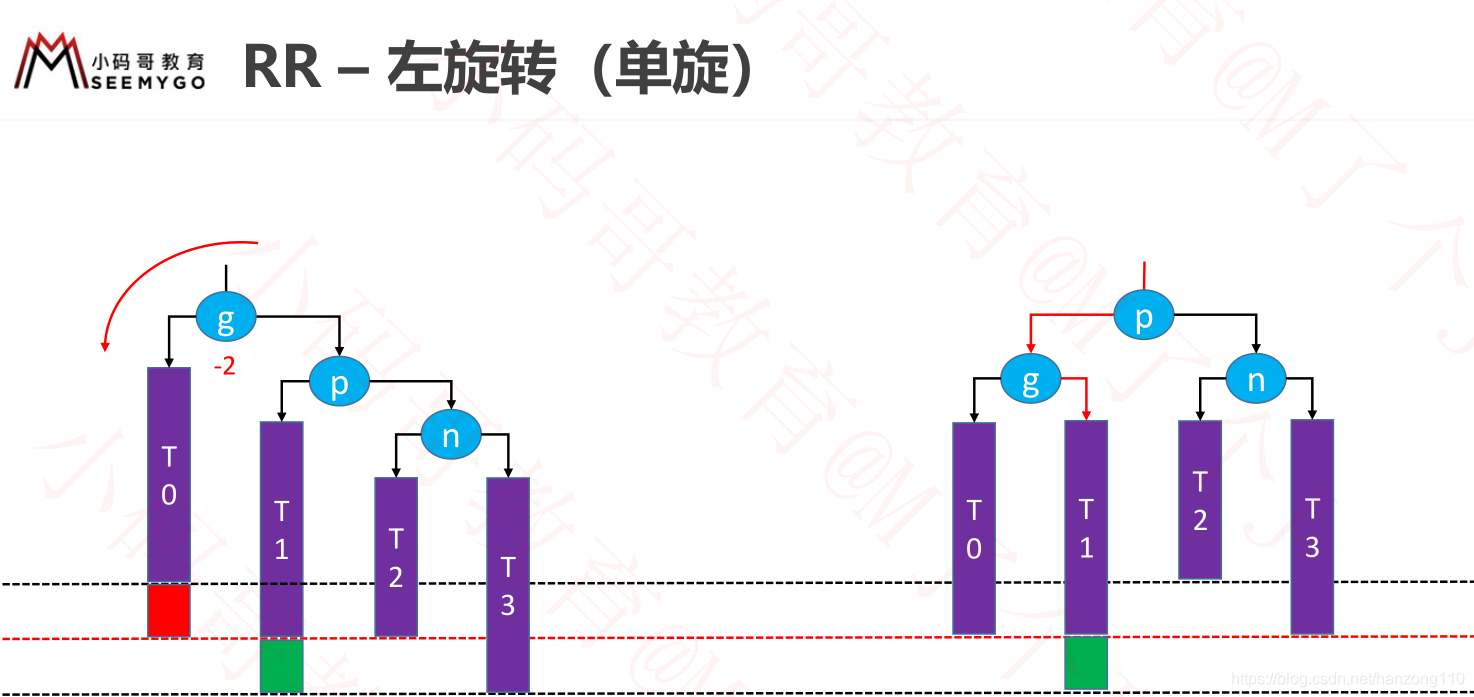
- RR:g右边是p,p右边是n,让g左旋转
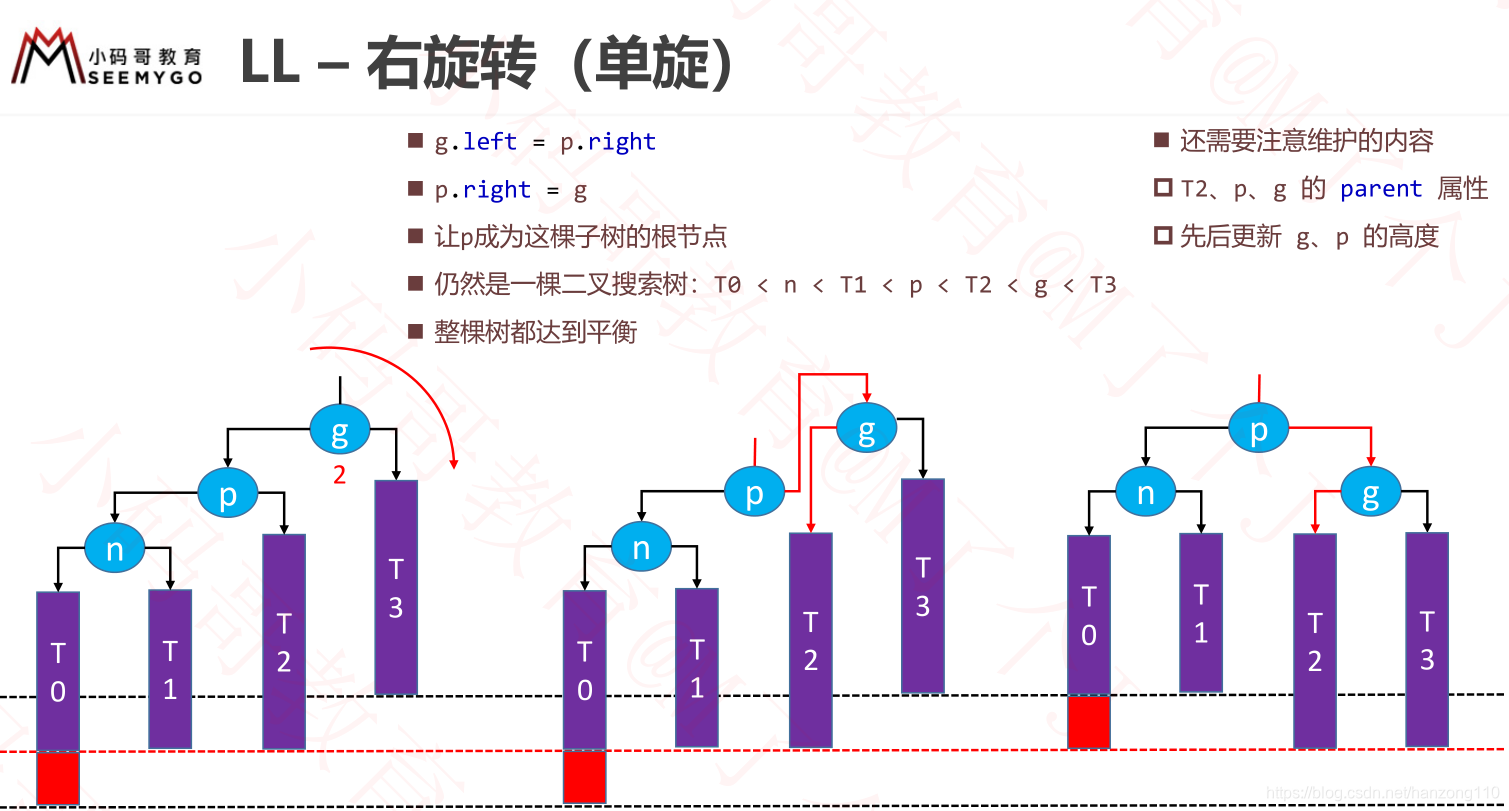
- LL:g左边是p,p左边是n,让g右旋转
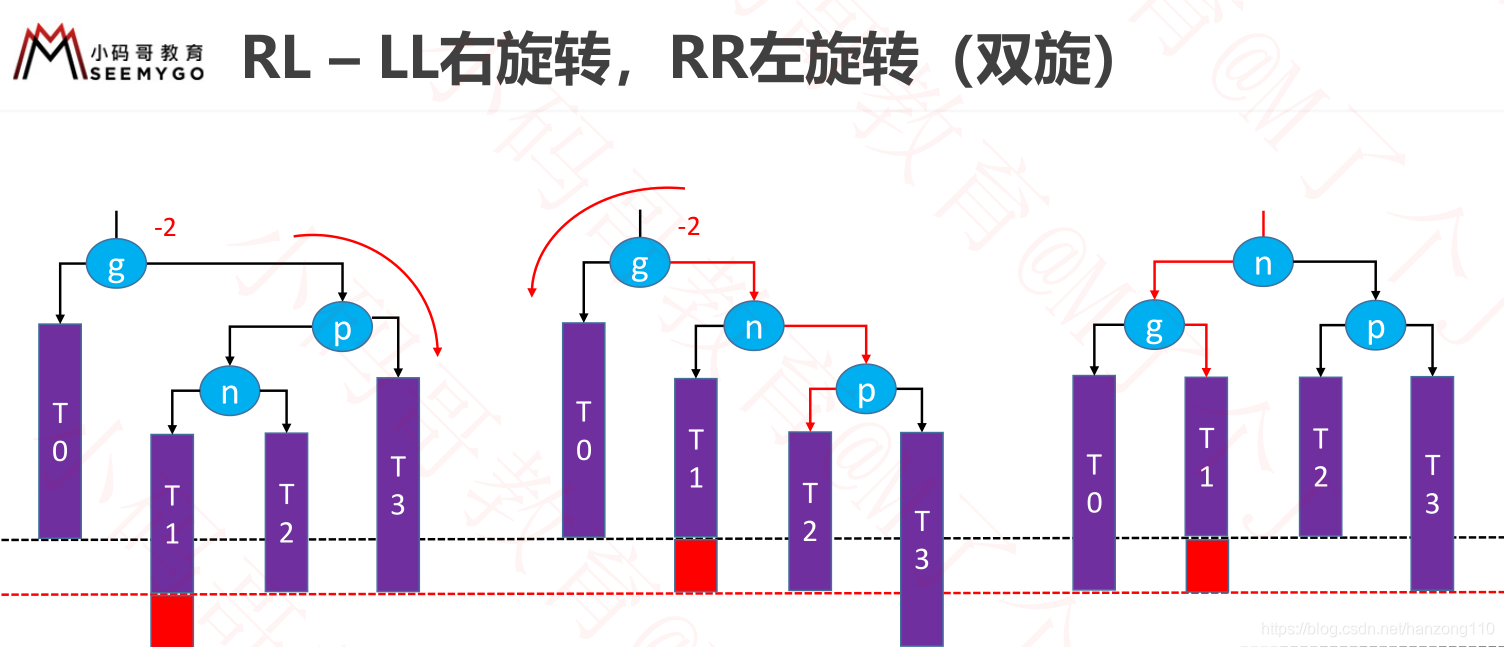
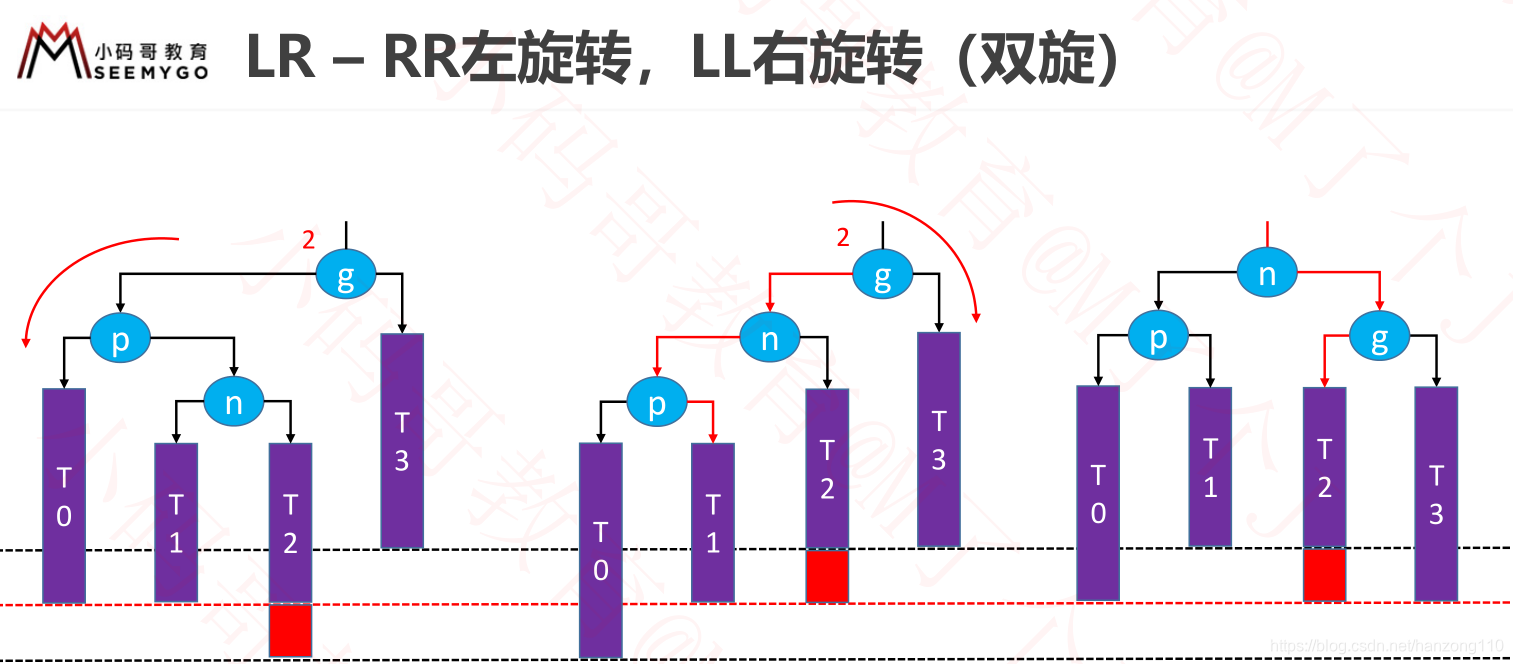
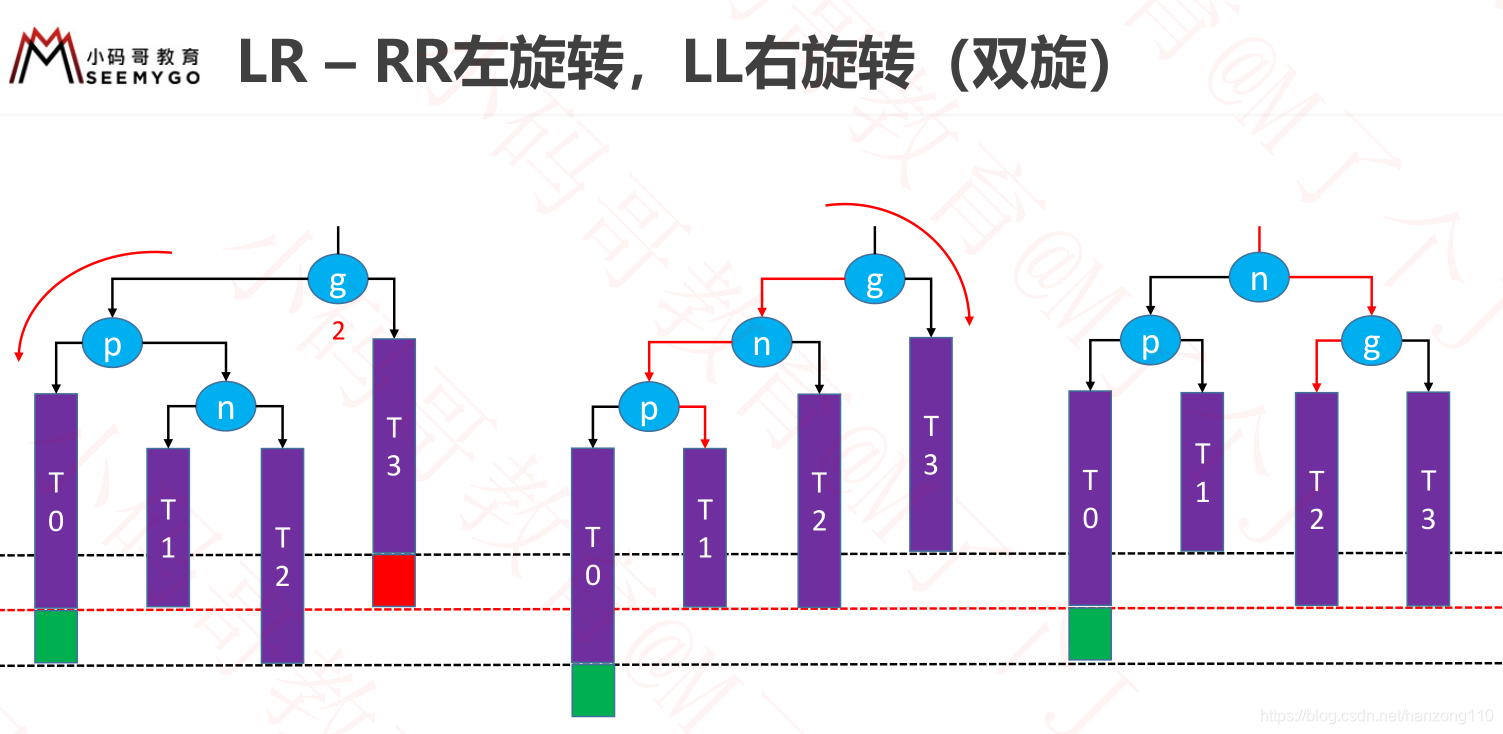
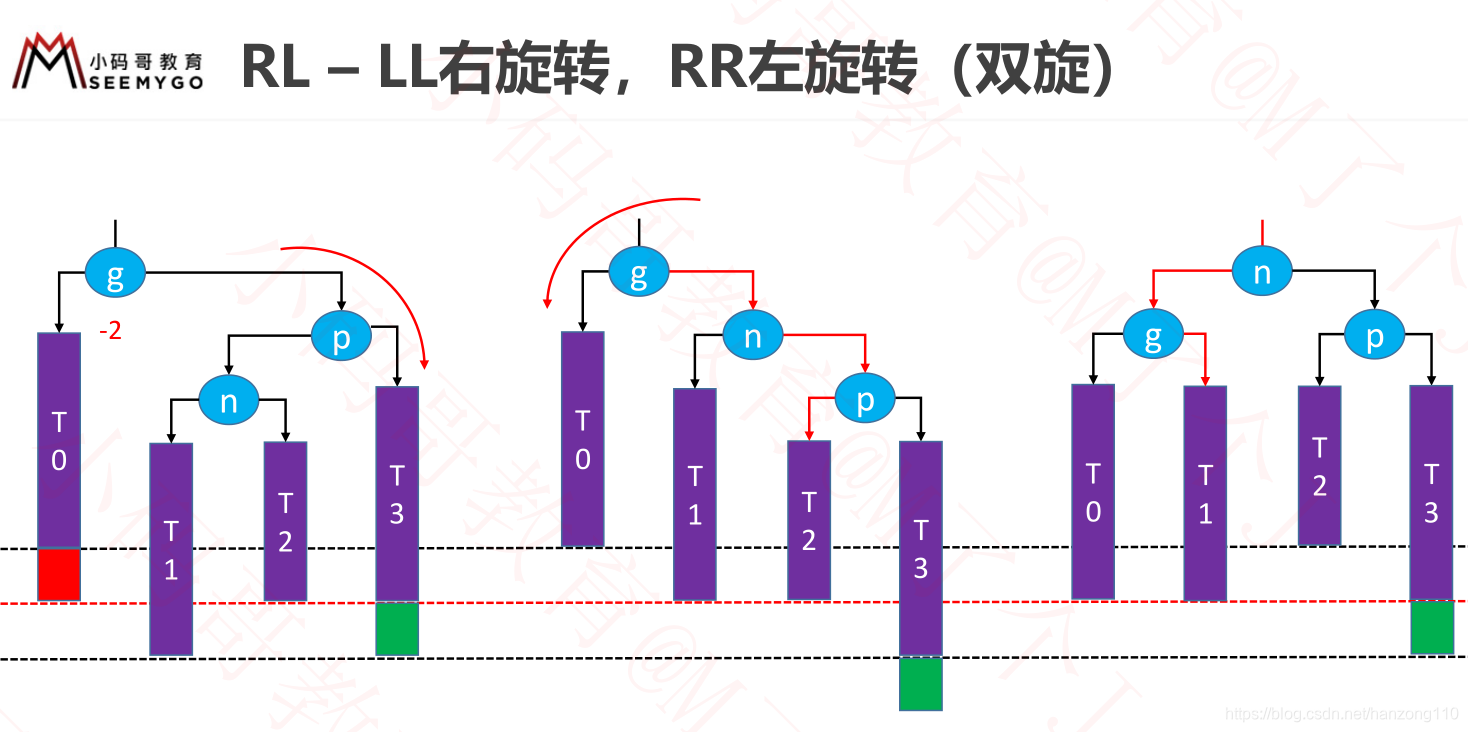
- LR:g左边是p,p右边是n,先让p左旋转变为LL,再让g右旋转
- RL:g右边是p,p左边是n,先让p右旋转变为RR,再让g左旋转
- 旋转的本质(左旋转为例)
- 当需要对grand节点旋转时,需要先获取grand节点的右边节点parent,因为左旋转,一定是围绕着右子节点旋转
- 然后要获得右子节点的左子节点child,因为这个节点要改变位置
- 让grand的左侧指向child
- 让parent的右侧指向grand
- 更新parent和高度
- 更新parent和高度的本质
- 当grand旋转后,需要更新grand、parent、child三者的parent属性,因为他们的parent都发生了变化
- 同时grand和parent的高度会发生变化,所以需要更新他们的高度
6.2 删除导致的失衡处理
- 删除导致失衡,一定是删除了某个节点A的子树中,高度最低的那个中的节点,但很明显这不会改变该A节点的高度,因此删除只会导致父节点或祖先节点中的某一个节点失衡,其他节点都不会失衡
- 删除时,为了调整平衡,也会进行旋转,旋转会降低较高子树的高度,因此可能导致更高层的祖先节点失衡,需要再次调整平衡
- 极端情况下,所有祖先节点都需要进行恢复平衡的操作,共 O(logn) 次调整
- afterRemove和afterAdd相比,只是去掉了恢复平衡后的退出循环即可

6.3 总结
- 搜索:O(logn)
- 添加:O(logn),仅需 O(1) 次的旋转操作
- 删除:O(logn),最多需要 O(logn) 次的旋转操作
6.4 代码
package com.mj.tree;
import java.util.Comparator;
public class AVLTree<E> extends BST<E> {
public AVLTree() {
this(null);
}
public AVLTree(Comparator<E> comparator) {
super(comparator);
}
@Override
protected void afterAdd(Node<E> node) {
while ((node = node.parent) != null) {
if (isBalanced(node)) {
// 更新高度
updateHeight(node);
} else {
// 恢复平衡
rebalance(node);
// 整棵树恢复平衡
break;
}
}
}
@Override
protected void afterRemove(Node<E> node) {
while ((node = node.parent) != null) {
if (isBalanced(node)) {
// 更新高度
updateHeight(node);
} else {
// 恢复平衡
rebalance(node);
}
}
}
@Override
protected Node<E> createNode(E element, Node<E> parent) {
return new AVLNode<>(element, parent);
}
/**
* 恢复平衡
* @param grand 高度最低的那个不平衡节点
*/
@SuppressWarnings("unused")
private void rebalance2(Node<E> grand) {
Node<E> parent = ((AVLNode<E>)grand).tallerChild();
Node<E> node = ((AVLNode<E>)parent).tallerChild();
if (parent.isLeftChild()) { // L
if (node.isLeftChild()) { // LL
rotateRight(grand);
} else { // LR
rotateLeft(parent);
rotateRight(grand);
}
} else { // R
if (node.isLeftChild()) { // RL
rotateRight(parent);
rotateLeft(grand);
} else { // RR
rotateLeft(grand);
}
}
}
/**
* 恢复平衡
* @param grand 高度最低的那个不平衡节点
*/
private void rebalance(Node<E> grand) {
Node<E> parent = ((AVLNode<E>)grand).tallerChild();
Node<E> node = ((AVLNode<E>)parent).tallerChild();
if (parent.isLeftChild()) { // L
if (node.isLeftChild()) { // LL
rotate(grand, node, node.right, parent, parent.right, grand);
} else { // LR
rotate(grand, parent, node.left, node, node.right, grand);
}
} else { // R
if (node.isLeftChild()) { // RL
rotate(grand, grand, node.left, node, node.right, parent);
} else { // RR
rotate(grand, grand, parent.left, parent, node.left, node);
}
}
}
private void rotate(
Node<E> r, // 子树的根节点
Node<E> b, Node<E> c,
Node<E> d,
Node<E> e, Node<E> f) {
// 让d成为这棵子树的根节点
d.parent = r.parent;
if (r.isLeftChild()) {
r.parent.left = d;
} else if (r.isRightChild()) {
r.parent.right = d;
} else {
root = d;
}
//b-c
b.right = c;
if (c != null) {
c.parent = b;
}
updateHeight(b);
// e-f
f.left = e;
if (e != null) {
e.parent = f;
}
updateHeight(f);
// b-d-f
d.left = b;
d.right = f;
b.parent = d;
f.parent = d;
updateHeight(d);
}
private void rotateLeft(Node<E> grand) {
Node<E> parent = grand.right;
Node<E> child = parent.left;
grand.right = child;
parent.left = grand;
afterRotate(grand, parent, child);
}
private void rotateRight(Node<E> grand) {
Node<E> parent = grand.left;
Node<E> child = parent.right;
grand.left = child;
parent.right = grand;
afterRotate(grand, parent, child);
}
private void afterRotate(Node<E> grand, Node<E> parent, Node<E> child) {
// 让parent称为子树的根节点
parent.parent = grand.parent;
if (grand.isLeftChild()) {
grand.parent.left = parent;
} else if (grand.isRightChild()) {
grand.parent.right = parent;
} else { // grand是root节点
root = parent;
}
// 更新child的parent
if (child != null) {
child.parent = grand;
}
// 更新grand的parent
grand.parent = parent;
// 更新高度
// 因为平衡的时候,高度已经更新了,此处旋转后高度变化,而其高度还未更新,所以需要重新更新高度
updateHeight(grand);
updateHeight(parent);
}
private boolean isBalanced(Node<E> node) {
return Math.abs(((AVLNode<E>)node).balanceFactor()) <= 1;
}
private void updateHeight(Node<E> node) {
((AVLNode<E>)node).updateHeight();
}
private static class AVLNode<E> extends Node<E> {
int height = 1;
public AVLNode(E element, Node<E> parent) {
super(element, parent);
}
public int balanceFactor() {
int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
return leftHeight - rightHeight;
}
public void updateHeight() {
int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
height = 1 + Math.max(leftHeight, rightHeight);
}
public Node<E> tallerChild() {
int leftHeight = left == null ? 0 : ((AVLNode<E>)left).height;
int rightHeight = right == null ? 0 : ((AVLNode<E>)right).height;
if (leftHeight > rightHeight) return left;
if (leftHeight < rightHeight) return right;
return isLeftChild() ? left : right;
}
@Override
public String toString() {
String parentString = "null";
if (parent != null) {
parentString = parent.element.toString();
}
return element + "_p(" + parentString + ")_h(" + height + ")";
}
}
}





















 999
999











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








