放苹果（递归）

题目：

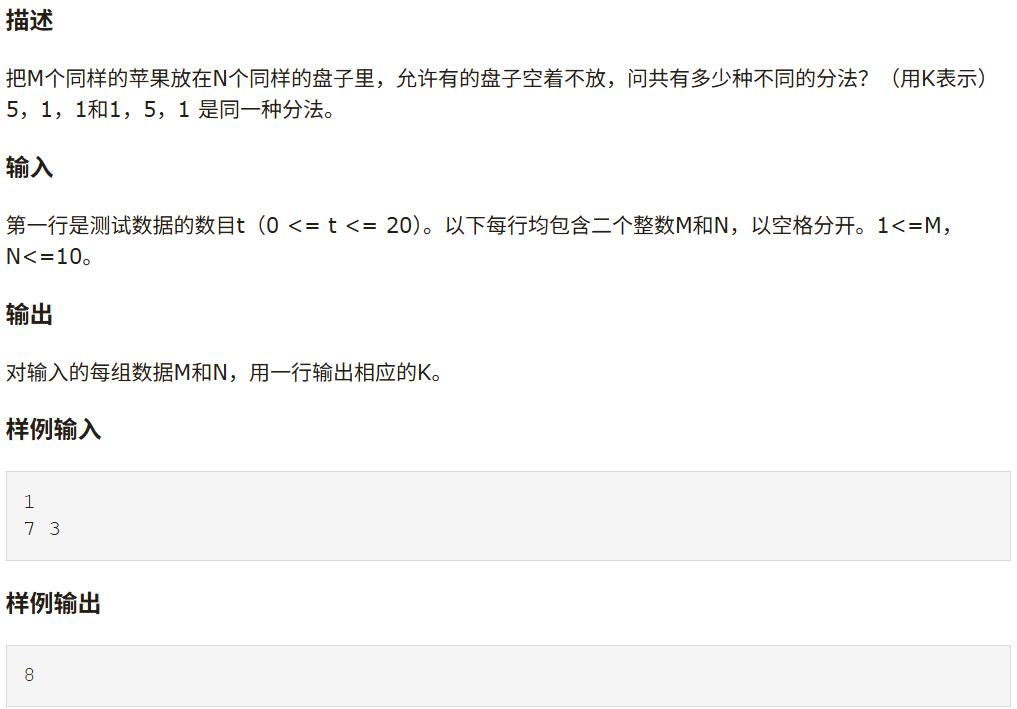
思路：
用递归求解。状态转移逻辑为：countWays(m, n-1) + countWays(m-n, n)，即前一种情况为至少有一个盘子为空，于是变成了m个苹果放n-1个盘子；后一种情况为没有盘子为空，于是每个盘子先放一个，然后再放剩下的苹果。

边界条件：

（1）苹果放完了（0个苹果），或者盘子只有1个，只有一种放法

（2）m-n可能导致苹果数小于0，直接返回0（也可以用if语句比较mn替换，如果m<n，返回countWays(m,m))

代码：

#include<iostream>
#include<vector>
using namespace std;

int countWays(int m, int n)
{
    if (m < 0)
        return 0;
    if (m == 0 || n == 1)
        return 1;

    return countWays(m, n - 1) + countWays(m - n, n);
}

int main()
{
    int t, m, n;
    cin >> t;
    while (t--)
    {
        cin >> m >> n;
        cout << countWays(m, n) << endl;
    }
    return 0;
}

错误的递归逻辑：

countWays(m-1, n) + countWays(1, n)

即先放n-1个苹果再放剩下的一个苹果，但是这种按照过程特征来构建的状态转移逻辑容易出现重复的错误，比如有2个苹果3个盘子，先放一个再放另一个会出现110、011、101的重复错误。应该按结果特征构建状态转移逻辑，我们最终关心的是苹果如何放到盘子中，而不是每一步怎么放，两个子状态要不重叠、不遗漏、穷尽所有情况。