EM算法与GMM的训练应用

注：本文主要参考Andrew Ng的Lecture notes 8，并结合自己的理解和扩展完成。本文有的数学推导过程并不是那么的严密，主要原因是本文的目的在于理解原理，若数学推导过于严密则文章会过于冗长。

GMM简介

GMM(Gaussian mixture model) 混合高斯模型在机器学习、计算机视觉等领域有着广泛的应用。其典型的应用有概率密度估计、背景建模、聚类等。

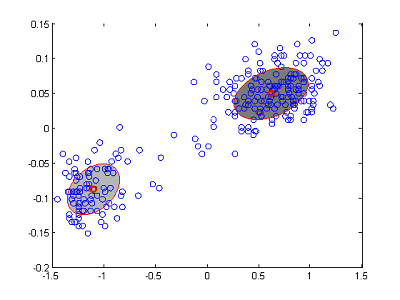
图1 GMM用于聚类

图2 GMM用于概率密度估计

图3 GMM用于背景建模

我们以聚类为例子进行简单讨论。如图1所示，假设我们有m个样本点，其坐标数据为{ $x^{(1)}$,$x^{(2)}$,$x^{(3)}$,…,$x^{(m)}$}(注：$x^{(i)}$为向量)。假设m个数据分别属于k个类别(图1中k=2)，且不知道每个样本点$x^{(i)}$属于哪一个类。假设每个类的分布函数都是高斯分布，那我们该如何求得每个点所属的类别?以及每个高斯分量的参数？我们先尝试最大似然估计。

回顾最大似然估计(MLE)的思想：已经出现的样本，应该是出现概率最大的样本。有似然函数： $$L(\theta)=\prod_ {i=1}^mp(x^{(i)},z^{(i)};u,\Sigma,\phi)$$

$L(\theta)$就是当前m个样本出现个概率，我们使其最大化就得到了$\theta$的估计值${\hat \theta}$;$p(x^{(i)},z^{(i)};u,\Sigma,\phi)$是样本$x^{(i)}$出现的概率；$z^{(i)}$是指第i属于z类；u是高斯分布的均值；$\Sigma$是高斯分布的方差；$\phi$为其他参数。为计算方便，对上式两边取对数，得到对数似然函数。

$$\begin{aligned} l(\theta) & =log(L(\theta)) \\ & =log(\prod_ {i=1}^mp(x^{(i)},z^{(i)};u,\Sigma,\phi)) \\ & =\sum_{i=1}^mlog(p(x^{(i)},z^{(i)};u,\Sigma,\phi)) \end{aligned}$$

上说道，GMM的表达式为k个高斯分布的叠加，所以有

$$p(x^{(i)},z^{(i)};u,\Sigma,\phi)=\sum_{z^{(i)}=1}^mp(x^{(i)}|z^{(i)};u_{z^{(i)}},\Sigma_{z^{(i)}})p(z^{(i)};\phi)$$

$p(z^{(i)};\phi)$为$p(z^{(i)})$为$z^{(i)}$的先验概率。上式中x和z为自变量；$u,\Sigma,\phi$为需要估计的参数。$p(x^{(i)} |z^{(i)};u_{z^{(i)}},Σ_{z^{(i)}} )$为高斯分布我们可以写出解析式，但是$p(z^{(i)};\phi)$的形式是未知的。所以不能直接对$l(\theta)$求偏导取极值。考虑到$z^{(i)}$不能直接由观测得到，称其为隐藏变量(latent variable)。此时的参数估计问题可以写为下式

$$argmaxl(\theta)=argmax\sum_{i=1}^mlog(\sum_{z^{(i)}=1}^mp(x^{(i)}|z^{(i)};u_{z^{(i)}},\Sigma_{z^{(i)}})p(z^{(i)};\phi))$$

为了求解上式，引入EM算法(Expectation-Maximization Algorithm)。我们从Jensen不等式开始讨论EM算法。

Jensen不等式

若实函数f(x)存在二阶导$f^{''}(x)$且有$f^{''}(x)≥0$，则f(x)为凸函数(convex function 注：此处的定义可能与国内教材不同)。$f(x)$的值域为$I$，则对于 $$a,b∈I,\, 0≤λ≤1$$ 有以下不等式成立：

f(λa+(1−λ)