一、条件概率公式
举个例子,比如让你背对着一个人,让你猜猜背后这个人是女孩的概率是多少?直接猜测,肯定是只有50%的概率,假如现在告诉你背后这个人是个长头发,那么女的概率就变为90%。所以条件概率的意义就是,当给定条件发生变化后,会导致事件发生的可能性发生变化。
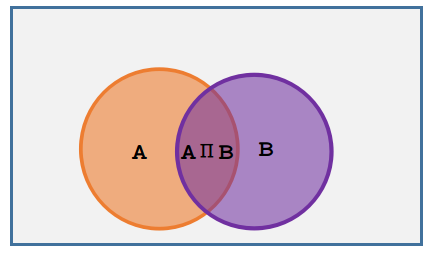
条件概率由文氏图出发,比较容易理解:
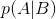
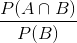
由:
得:
这就是条件概率公式。
假如事件A与B相互独立,那么:
注:
相互独立:表示两个事件发生互不影响。而互斥:表示两个事件不能同时发生,(两个事件肯定没有交集)。互斥事件一定不独立(因为一件事的发生导致了另一件事不能发生);独立事件一定不互斥,(如果独立事件互斥, 那么根据互斥事件一定不独立,那么就矛盾了),但是在概率形式上具有一些巧合性,一般地:
但是,对于两个独立事件,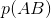
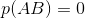
二、全概率公式
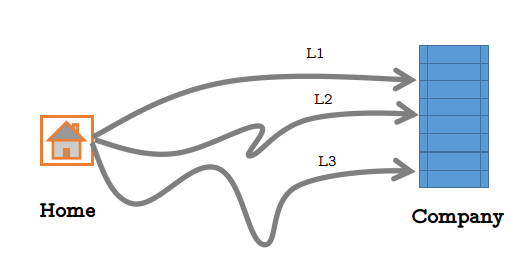
先举个例子,小张从家到公司上班总共有三条路可以直达(如下图),但是每条路每天拥堵的可能性不太一样,由于路的远近不同,选择每条路的概率如下:
每天上述三条路不拥堵的概率分别为:
假设遇到拥堵会迟到,那么小张从Home到Company不迟到的概率是多少?
其实不迟到就是对应着不拥堵,设事件C为到公司不迟到,事件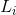
全概率就是表示达到某个目的,有多种方式(或者造成某种结果,有多种原因),问达到目的的概率是多少(造成这种结果的概率是多少)?
全概率公式:
设事件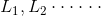
那么就称这个公式为全概率公式。
三、贝叶斯公式
仍旧借用上述的例子,但是问题发生了改变,问题修改为:到达公司未迟到选择第1条路的概率是多少?
可不是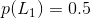
故有:
所以选择第一条路的概率为0.28.
贝叶斯公式就是当已知结果,问导致这个结果的第i原因的可能性是多少?执果索因!
贝叶斯公式:
在已知条件概率和全概率的基础上,贝叶斯公式是很容易计算的:








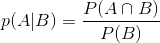
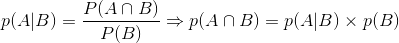
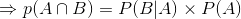
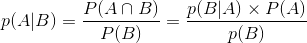
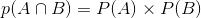
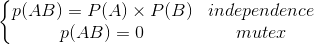
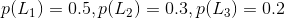
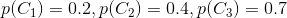
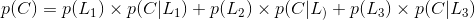
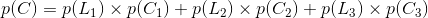
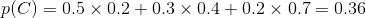
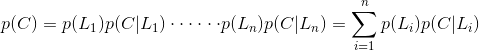
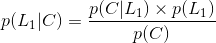
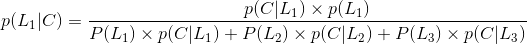
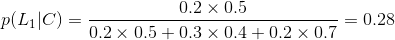
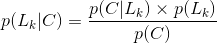













 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








