KNN算法

K nearest neighbours - K最近邻分类法
转载自该博客
K最近邻密度估计是一种分类方法，不是聚类方法
规则：
1、计算待分类数据和不同类中每一个数据的距离（欧式或马氏）
（1）欧式距离为在m维空间中两点的真实距离：
$distance = \sqrt {(\sum_{i=1}^n x_{i1}^2 - x_{i2}^2)}, i=1,2,\cdots$
（2）马氏距离为数据的协方差距离，是一种有效的计算两个未知样本集的相似度的方法，与欧氏距离的不同之处在于它考虑到各种特性之间的联系，并且是尺度无关的（即独立于测量尺度）。
对一个均值为$\mu = (\mu_1,\mu_2,\mu_3,\cdots,\mu_p)^T$，协方差矩阵为$\sum$的多变量向量$x = (x_1,x_2,x_3,\cdots,x_p)^T$ ,其马氏距离为：
$D_M(x) = \sqrt{(x-\mu)^T\sum^{-1}(x-mu)}$
（3）协方差在概率论和统计学中用于衡量两个变量的总体误差，而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
期望值分别为$E(X) = \mu ,E(Y) = \nu$的两个实数随机变量$X,Y$之间的协方差定义为：
$cov(X,Y) = E((X - \mu)(Y-\nu))$
$cov(X,Y) = E(X\cdot Y) - \mu\nu$
2、选出最小的前k个，选择排序、或堆排序、或者kd-tree（待查）
3、对比前k个距离，找出k个数据中包含最多的是哪类数据，即为待分类数据所在的类。

注意：
1、在N个训练向量，不考虑类的标签来确定K邻近。在两类的情况下，K选为奇数，一般不是类的个数的倍数。
2、在K个样本之外，确定属于$W_i,i = 1,2,\cdots,M$类的向量的个数$K_i$，显然$\sum(K_i) = k$
3、X属于样本最大值$K_i$的哪一类$W_i$

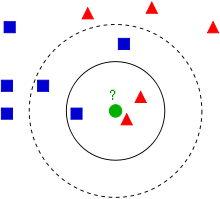
如下图，绿色的值为待分类，3NN则属于三角，5NN则属于矩形

clear all;
close all;
clc;

%%第一个类数据和标号
mu1=[0 0];  %均值
S1=[0.3 0;0 0.35];  %协方差
data1=mvnrnd(mu1,S1,100);   %产生高斯分布数据
plot(data1(:,1),data1(:,2),'+');
label1=ones(100,1);
hold on;

%%第二个类数据和标号
mu2=[1.25 1.25];
S2=[0.3 0;0 0.35];
data2=mvnrnd(mu2,S2,100);
plot(data2(:,1),data2(:,2),'ro');
label2=label1+1;

data=[data1;data2];
label=[label1;label2];

K=11;   %两个类，K取奇数才能够区分测试数据属于那个类
%测试数据，KNN算法看这个数属于哪个类
for ii=-3:0.1:3
    for jj=-3:0.1:3
        test_data=[ii jj];  %测试数据
        label=[label1;label2];
        %%下面开始KNN算法，显然这里是11NN。
        %求测试数据和类中每个数据的距离，欧式距离（或马氏距离） 
        distance=zeros(200,1);
        for i=1:200
            distance(i)=sqrt((test_data(1)-data(i,1)).^2+(test_data(2)-data(i,2)).^2);
        end

        %选择排序法，只找出最小的前K个数据,对数据和标号都进行排序
        for i=1:K
            ma=distance(i);
            label_ma = label(i);%在博客原文上添加该语句
            for j=i+1:200
                if distance(j)<ma
                    ma=distance(j);
                    label_ma=label(j);
                    tmp=j;
                end
            end
            distance(tmp)=distance(i);  %排数据
            distance(i)=ma;

            label(tmp)=label(i);        %排标号，主要使用标号
            label(i)=label_ma;
        end

        cls1=0; %统计类1中距离测试数据最近的个数
        for i=1:K
           if label(i)==1
               cls1=cls1+1;
           end
        end
        cls2=K-cls1;    %类2中距离测试数据最近的个数

        if cls1>cls2    
           plot(ii,jj);     %属于类1的数据画小黑点
        end

    end
end

“`