RC低通滤波电路直接带载后会发生什么？

1、滤波的含义

滤波是频域范畴，它说的是不同频率的信号经过一个电路处理后，信号发生变化的问题，变化包含了原始信号幅值和相位的变化，滤波电路对信号的幅值做出的响应称为幅频响应，对信号相位做出的反应称为相频响应。每一个频率的信号对应在时域就是信号的充放电特性。

滤波通常借助动态器件如电感和电容，利用它们在不同频率下阻抗变化，从而在其上面产生压降，对我们需要去除的信号进行衰减，从而达到滤波的效果。

我们知道电感和电容的阻抗特性其实就是储能特性，储能意味着时间特性，需要过程，这个过程是滤波特性的体现的一方面。

2、分析方法和工具

在s域，写出回路的传递函数，根据波特图进行分析，传递函数是输入和输出的增益关系

为了同时分析相位和幅值引入虚数，并且在虚平面进行分析，和频率相关的电路阻值特性，我们用阻抗描述，通常包含实部与虚部，这个数学工具的引入，包含了幅值和相位信息的体现，简化了分析难度。

角速度描述表示

注：

由于自然界正弦信号认为是单一频率的信号，是基础信号，不可再分解，其它信号是以正弦为基础的合成信号，所以，以下从电路输入某个频率的正弦信号开始分析。正弦信号输入这些线性电路，达到稳定后，输出信号只会发生幅值和相位的改变，不改变信号的频率。

3、RC低通滤波电路结构和特性

（1）RC滤波电路，图中包含了这个电路的传递函数G(s)表达式

RC滤波电路

从传递函数解出一个称作为极点的根，即令传递函数的分母为零，最后得出一个频率，由于这个频率从波特图上看，曲线在这个点前后发生突变的现象，我们形象地将这个频率称为“转折频率”，转折频率意味着一个响应发生“突变”的频率点，转折意味着响应的转弯点，前后会发生较大的变化。记住波特图图横轴是频率，代表着一系列不同频率信号通过这个电路后，输出会发生不一样的变化，是一系列的信号，不是单一信号。转折频率代表了电路的固有特性，是电路参数和结构导致的结果，是电路的固有属性。

RC的转折频率

借助matalab工具进行绘制响应曲线，其它工具也可以，只要是自己熟悉的工具即可

下面我们对R和C赋值，R=100Ω，C1=100uF，得到转折频率f=15.915Hz

syms s R C % 定义符号参量

R=100; C=100*10^-6;% 给分子分母赋值

G(s)=1/(s*R*C+1);% 传递函数表达式

num=[0,1];% 分子系数 den=[1/100,1];% 分母系数

G1=tf(num,den)% 得出传递函数

margin(G1)% 画出增益和相位裕量图

grid on;

% 得出传递函数为G(s)=1/(s/100 + 1)

RC的幅频和相频曲线

曲线说明

（1）直流增益，即低频增益，在传递函数中令s=0，得到直流增益为1，转换成dB刚好为0dB（0dB=20log1），这正是我们无源器件低通滤波器的特点，不能放大信号，在低频段，电容容抗几乎为无穷大，即电容为开路状态，信号被原模原样传输过来，这时候增益就是1，由于电容看做开路，那么阻性电路中，信号自然也不会产生任何相位偏移。

直流增益

（2）转折频率的地方，这个频率的信号增益被衰减到原来的70.7%，也就是-3dB的地方，图中为-2.99dB对应转折频率为15.9Hz，这是由于实际计算转折频率为15.915Hz，存在一点误差。对相位来说，在这个频率点，相位会偏移-45°，负号表示信号被滞后了，从时间看，也就是被延时了。但是对其它不同频率信号在这个频率点前后响应出现较大的不同。之前看做不衰减也就是直流增益部分，之后信号被快速衰减，同时产生一定的相移。

（3）延时时间计算，也就是相位延迟和具体时间的对应关系，方便我们理解相位和延迟之间的关系，延迟时间为：延迟时间=Kd*周期

延迟系数Kd，即在一个360°周期里延迟角度占有的比例，这里是45/360=1/8，也就是45°占有360°的1/8。

转折频率约为15.9Hz，即一个周期为62.89ms。

那么，输入信号被延时时间为62.89ms*1/8=7.86ms，输出信号晚来输入信号7.86ms。

如下是对一个100Hz和200Hz信号进行延时举例，也说明了相位差和时间差之间的关联，它们一一对应（one to one）

相位延迟的含义表示

用TINA仿真进行波形验证，借助仿真软件验证你的结果，并且可以帮助你理解

RC仿真电路

相比于输入信号Uin，稳态后，电容电压为输出信号被滞后45°，并且幅度被衰减到70.7%，从下图波形也可以看出。（稳态后，电阻上电压超前了45°，想象一下，这个电路测量对象不同，带来了“高通”和“低通”的概念）

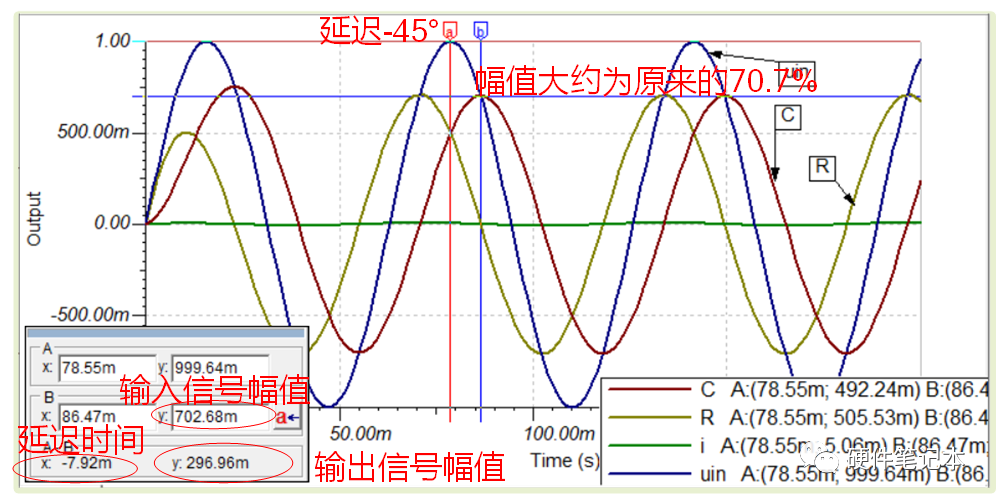
仿真波形

4、直接带载后会发生什么？

如下图，我们将R2放置在电路中，模拟一个负载

带载的RC电路

我们再次借助MATLAB化简方程

%zo输出阻抗，是电容C1和电阻R2的并联值 % z是电路总阻抗 % G(s)传递函数

syms R1 R2 C1

zo=R2/(s*C1*R2+1); z=R1+zo;

G(s)=zo/z; G1(s)=simplify(G(s))%化简代数式

最后得出传递函数为G(s)=G1(s)=R2/(R1 + R2 + C1*R1*R2*s)

同时令传递函数的分母为零解出极点，如上图，我们可以把它写作为频率的形式，这个频率在波特图中正好是转折频率，我们利用MATLAB进行验证

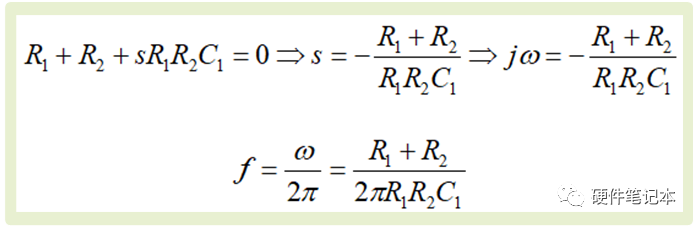
带载后RC电路的转折频率

转折频率处，输出信号相比输入信号，输入信号的幅值被衰减到原来的70.7%，相位被滞后45°（图中就是-45，符号表示信号相位被滞后）

下面我们对R1、R2和C1赋值，R1=100Ω、R2=20Ω，C1=100nF

syms R1 R2 C1 s

R1=100;R2=20;C1=100*10^-9;

zo=R2/(s*C1*R2+1); z=R1+zo;

G(s)=zo/z;

G1(s)=simplify(G(s))%化简代数式

% G(s)=G1(s)=R2/(R1 + R2 + C1*R1*R2*s)

%得到传递函数表达式 G(s)=G1(s)=100000/(s+600000)

num=[0,100000]; den=[1,600000];

G1=tf(num,den)% 得到传递函数

margin(G1)

grid on;

最终得到幅频和相频特性图

幅频和相频特性图

（1）直流增益，也就是低频下的增益，我们对传递函数频率项s=0，那么就得到直流增益，这也是我们在做电源环路中分析中采取的方法得到直流增益。这里直流增益如下，也就是除去了时效性动态器件的影响，纯阻性表现的特性，就是一个简单的分压电路。

直流增益

注：1/6刚好是-15.6dB，负分贝表示信号被衰减

（2）转折频率处，我们经过简单计算，得到转折频率为f=95.49kHz，如下图，转折频率处信号衰减到原来的70.7%，即1/6*70%=0.1178，即为-18.6dB，波特图中可以看出，同时相位被滞后45°（-45℃）。

这个电路，我们对并联在C1上的R2取值为无限大，我们将R2取值无穷大后，只需要把传递函数简单化简后求极限，则电路重回到开头的RC电路，传递函数和RC低通电路相同。
 

转折频率

注：负载的直接接入导致转折频率会向右移，即转折频率比单纯的RC会偏高，若R2趋于∞，那么转折频率由95.49k变为15.92k（用Excel快速计算一下）。

实际中滤波电路该怎么样接负载

实际当中，尤其是采样电路，我们经常会用到RC低通滤波，我们会采用输入阻抗很大的运放组成跟随器。

在MCU中，采样输入端口往往也是阻抗很大，所以我们也可以直接用RC滤波进行直接接入

高输入阻抗端口，这些都是让我们想要的信号幅值不发生衰减，而且几乎不产生相移、设定的转折频率不发生偏移，信号能够被正常采集。