最长回文子串

输入一个字符串，输出该字符串中对称的子字符串的最大长度。

比如输入字符串“google”，由于该字符串里最长的对称子字符串是“goog”，因此输出4。

    1.由于回文可能由奇数个字符组成，也可能由偶数个字符组成。对奇数回文的处理比较直观，只需要以某个字符为中心，依次向两边扩展即可。因此，我们可以通过如下方式把对偶数回文的处理转换成对奇数回文的处理：在字符边界添加特殊符号。例如，对字符串aba，预处理后变成#a#b#a#；对字符串abba，预处理后变成#a#b#b#a#。可以看出，不管是奇数回文，还是偶数回文，在与处理后都变成奇数回文。在找出与预处理后字符串的最长回文后，只需要去除所有的#即为源字符串的最长回文。

    2.对寻找字符串某类子串的问题，最简单直观的想法就是穷举出所有子串一一进行判别。这里也不例外，当然时间复杂度也很高，为O（n^3）。

    3.对该问题，我们可以进行一定程度的简化处理。既然回文是一种特殊的字符串，我们可以以源字符串的每个字符为中心，依次寻找出最长回文子串P0, P1,...,Pn。这些最长回文子串中的最长串Pi = max(P1, P2,...,Pn)即为所求。请看源码：

string find_lps_native(const string &str)
{
    int center = 0, max_len = 0;
    for(int i = 1; i < str.length()-1; ++i)
    {
        int j = 1;
        //以str[i]为中心，依次向两边扩展，寻找最长回文Pi
        while(i+j < str.length() && i-j >= 0 && str[i+j] == str[i-j])
            ++j;
        --j;
        if(j > 1 && j > max_len)
        {
            center = i;
            max_len = j;
        }
    }
    return str.substr(center-max_len, (max_len << 1) + 1);
}

    4.可以看出，上面做法的复杂度为O（n^2）。相比穷举字符串的做法，已经降低了一个量级的复杂度。但是仔细想想，上面的算法还有改进空间吗？当然有！而且改进后能够把复杂度降低到O（n）！这就是大名鼎鼎的 Manacher’s Algorithm。请看下文分析：

    先在每两个相邻字符中间插入一个分隔符，当然这个分隔符要在原串中没有出现过。一般可以用‘#’分隔。这样就非常巧妙的将奇数长度回文串与偶数长度回文串统一起来考虑了（见下面的一个例子，回文串长度全为奇数了），然后用一个辅助数组P记录以每个字符为中心的最长回文串的信息。P［id］记录的是以字符str［id］为中心的最长回文串的半径（包含str［id］本身）。
    原串：   waabwswfd
    新串：   # w # a # a # b # w # s # w # f # d #
辅助数组P：  1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1
    这里有一个很好的性质，P［id］-1就是该回文子串在原串中的长度（包括‘#’）。

    对字符串S=abcdcba而言，最长回文子串是以d为中心，半径为3的子串。当我们采用上面的做法分别求出以S[1]=a, S[2]=b, S[3]=c, S[4]=d为中心的最长回文子串后，对S[5]=c,S[6]=b...还需要一一进行扩展求吗？答案是NO。因为我们已经找到以d为中心，半径为3的回文了，S[5]与S[3]，S[6]与S[2]...，以S[4]为对称中心。因此，在以S[5],S[6]为中心扩展找回文串时，可以利用已经找到的S[3],S[2]的相关信息直接进行一定步长的偏移，这样就减少了比较的次数（回想一下KMP中next数组的思想）。优化的思想找到了，我们先看代码：

//输入，并处理得到字符串s
int p[1000], mx = 0, idx = 0;
memset(p, 0, sizeof(p));
for (i = 1; s[i] != '\0'; i++) {
    p[i] = mx > i ? min(p[2*idx-i], mx-i) : 1;
    while (s[i + p[i]] == s[i - p[i]]) p[i]++;
    if (i + p[i] > mx) {
        mx = i + p[i];
        idx = i;
    }
}
//找出p[i]中最大的

          这里进行简单的解释：上述代码中有三个主要变量，它们代表的意义分别是：

     p:以S[i]为中心的最长回文串的半径为p[i]。

    idx:已经找出的最长回文子串的起始位置。

   mx:已经找出的最长回文子串的结束位置。

    算法的主要思想是：先找出所有的p[i]，最大的p[i]即为所求。在求p[j] （j>i）时，利用已经求出的p[i]减少比较次数。代码中比较关键的一句是：p[i] = mx > i ? min(p[2*idx-i], mx-i) : 1;

    在求p[i]时：

    如果 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配；

    如果 mx>i，则表明已经求出的最长回文中包含了p[i]，那么与p[i]关于idx对称的p[ (idx << 1) - i]的最长回文子串可以提供一定的信息：

    当P[id]+id=mx>i 时说明以i为中心点可能存在回文子串，这时就可以将P[i]初始化成该回文子串的值在进行扩展搜索回文子串的半径是否能够增大，省去了P[i]从0开始搜索的一些步骤。

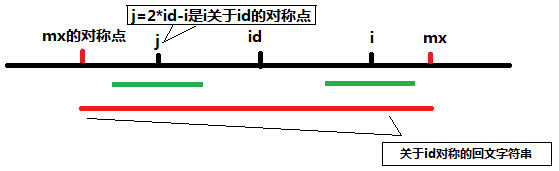
    A:mx-i>P[j]的情形。这时的字符串可以表示成下图（注意到j=2*id-1）：

     

    图中最下面的红色线条是之前求得的索引号i之前的那个使得回文子串最右面的字符的索引号最大的那个回文子字符串。j点是i关于id的对称点，由于红的字符串是回文字符串，所以关于j对称的回文子串和关于i对称的回文子串是完全一样的(图中两段绿色的线条)，而满足mx-i>P[j]时说明此时j的回文子串半径小于j到mx关于j对称的左端点的差，此时可以初始化P[i]=P[j]。

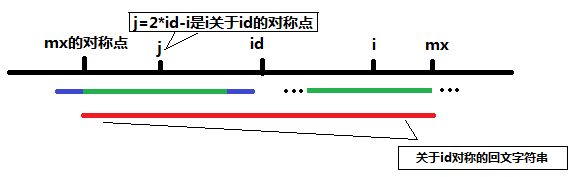
    B：mx-i<=P[j]的情形。这时的字符串可以表示成下图：

     

    图中最下面的红色线条仍然是之前求得的索引号i之前的那个使得回文子串最右面的字符的索引号最大的那个回文子字符串。j点是i关于id的对称点，由于红的字符串是回文字符串，所以关于j对称的回文子串和关于i对称的在mx和mx的对称点之间的回文子串是完全一样的(图中两段绿色的线条)，而满足mx-i<=P[j]时说明此时j的回文子串半径大于或等于j到mx关于j对称的左端点的差，此时可以先初始化P[i]=mx-i，然后再对P[i]的回文子串半径进行进一步的增大。

   5.除了上述的几种做法外，还可以利用动态规划来进行求解。

   DP的考虑源于暴力方法，暴力方法是寻找一个字符串的所有子串，需要O(n^2)的开销，然后对于每一个子串需要O(n)的开销来判断是否是回文，故暴力方案为O(n^3)，但是这里有一个问题，就是在暴力的时候有重复判断；

    例如，如果子串X为回文，那么sXs也是回文；如果X不是回文，那么sXs也不是回文；另外，ss也是回文。所以这里使用DP我们可以按照子串长度从小到大的顺序来构建DP状态数组，使用一个二维数组dp[i][j]记录子串[i-j]是否为回文子串，那么我们就有初始化和自底向上的方案了；

    初始化：单字符串和相等的双字符串为回文

    自底向上构造：X[i]==X[j] && dp[i+1][j-1]==1 则dp[i][j] = 1

#include <iostream>
using namespace std;
 
/* 最长回文子串 LPS - DP */
 
int maxlen;  // LPS长度
 
/* DP解法 */
bool dp[31][31]; // dp[i][j]记录子串[i-j]是否构成回文
 
void LPS_dp(char * X, int xlen)   // 略去测试X合法性
{
    maxlen = 1;
 
    for(int i = 0; i < xlen; ++i) // 初始化
    {
        dp[i][i] = 1;       // 单字符为回文
        if(i && (X[i-1] == X[i]))
        {
            dp[i-1][i] = 1; // 双字符串为回文
        }
    }
 
    for(int len = 2; len < xlen; ++len)
    {
        for(int begin = 0; begin < xlen-len; ++begin)
        {
            int end = begin + len; // 从长度为3开始
 
            if((X[begin]==X[end]) && (dp[begin+1][end-1]==1))
            {
                dp[begin][end] = 1;
                if(end - begin + 1 > maxlen)
                {
                    maxlen = end - begin + 1;
                }
            }
        }
    }
}
 
void main()
{
    char X[30];  // 设串不超过30
    /* test case
     * abcfdcba / abba / abab / aaaa
     */
    while(cin.getline(X,30))
    {
        memset(dp,0,sizeof dp);
        /* DP方法 */
        LPS_dp(X,strlen(X));
        printf("%d\n", maxlen);
    }
}

参考资料

1. 程序员面试题精选100题(46)－对称子字符串的最大长度
    http://zhedahht.blog.163.com/blog/static/25411174201063105120425/

2. http://larrylisblog.net/WebContents/images/LongestPalindrom.pdf

3. 浅谈manacher算法：http://blog.sina.com.cn/s/blog_70811e1a01014esn.html

4. O(n)时间求字符串的最长回文子串：http://www.felix021.com/blog/read.php?2040

5、http://www.akalin.cx/longest-palindrome-linear-time

6、http://www.ahathinking.com/archives/132.html