分类目录:《机器学习中的数学》总目录
相关文章:
· 距离定义:基础知识
· 距离定义(一):欧几里得距离(Euclidean Distance)
· 距离定义(二):曼哈顿距离(Manhattan Distance)
· 距离定义(三):闵可夫斯基距离(Minkowski Distance)
· 距离定义(四):切比雪夫距离(Chebyshev Distance)
· 距离定义(五):标准化的欧几里得距离(Standardized Euclidean Distance)
· 距离定义(六):马氏距离(Mahalanobis Distance)
· 距离定义(七):兰氏距离(Lance and Williams Distance)/堪培拉距离(Canberra Distance)
· 距离定义(八):余弦距离(Cosine Distance)
· 距离定义(九):测地距离(Geodesic Distance)
· 距离定义(十): 布雷柯蒂斯距离(Bray Curtis Distance)
· 距离定义(十一):汉明距离(Hamming Distance)
· 距离定义(十二):编辑距离(Edit Distance,Levenshtein Distance)
· 距离定义(十三):杰卡德距离(Jaccard Distance)和杰卡德相似系数(Jaccard Similarity Coefficient)
· 距离定义(十四):Ochiia系数(Ochiia Coefficient)
· 距离定义(十五):Dice系数(Dice Coefficient)
· 距离定义(十六):豪斯多夫距离(Hausdorff Distance)
· 距离定义(十七):皮尔逊相关系数(Pearson Correlation)
· 距离定义(十八):卡方距离(Chi-square Measure)
· 距离定义(十九):交叉熵(Cross Entropy)
· 距离定义(二十):相对熵(Relative Entropy)/KL散度(Kullback-Leibler Divergence)
· 距离定义(二十一):JS散度(Jensen–Shannon Divergence)
· 距离定义(二十二):海林格距离(Hellinger Distance)
· 距离定义(二十三):α-散度(α-Divergence)
· 距离定义(二十四):F-散度(F-Divergence)
· 距离定义(二十五):布雷格曼散度(Bregman Divergence)
· 距离定义(二十六):Wasserstein距离(Wasserstei Distance)/EM距离(Earth-Mover Distance)
· 距离定义(二十七):巴氏距离(Bhattacharyya Distance)
· 距离定义(二十八):最大均值差异(Maximum Mean Discrepancy, MMD)
· 距离定义(二十九):点间互信息(Pointwise Mutual Information, PMI)
F-散度已经可以表达我们提到的所有散度,目前为止它是最通用的散度形式。但很多文章也会出现另一种叫做Bregman的散度,它和F-散度不太一样,是另一大类散度。
我们以欧几里得距离举例,即
n
n
n维空间中的欧几里得距离:
d
(
x
,
y
)
=
∑
i
=
1
n
(
x
i
−
y
i
)
2
d(x, y)=\sqrt{\sum_{i=1}^n(x_i-y_i)^2}
d(x,y)=i=1∑n(xi−yi)2
我们将其平方:
d
2
(
x
,
y
)
=
∑
i
=
1
n
(
x
i
−
y
i
)
2
d^2(x, y)=\sum_{i=1}^n(x_i-y_i)^2
d2(x,y)=i=1∑n(xi−yi)2
如果我们定义内积
<
x
,
y
>
=
∑
i
−
1
n
x
i
y
i
<x, y>=\sum_{i-1}^nx_iy_i
<x,y>=∑i−1nxiyi和欧式模
∣
∣
x
∣
∣
=
<
x
,
x
>
||x||=\sqrt{<x, x>}
∣∣x∣∣=<x,x>,则上式可以写为如下形式:
d
2
(
x
,
y
)
=
∑
i
=
1
n
(
x
i
−
y
i
)
2
=
<
x
−
y
,
x
−
y
>
=
∣
∣
x
∣
∣
2
−
(
∣
∣
y
∣
∣
2
+
<
2
y
,
x
−
y
>
)
d^2(x, y)=\sum_{i=1}^n(x_i-y_i)^2=<x-y, x-y>=||x||^2-(||y||^2+<2y, x-y>)
d2(x,y)=i=1∑n(xi−yi)2=<x−y,x−y>=∣∣x∣∣2−(∣∣y∣∣2+<2y,x−y>)
注意到,
2
y
2y
2y是
y
2
y^2
y2的导数,因此上式的后一项
(
∣
∣
y
∣
∣
2
+
<
2
y
,
x
−
y
>
(||y||^2+<2y, x-y>
(∣∣y∣∣2+<2y,x−y>是函数
f
(
z
)
=
∣
∣
z
∣
∣
2
f(z)=||z||^2
f(z)=∣∣z∣∣2在
y
y
y点的切线在
x
x
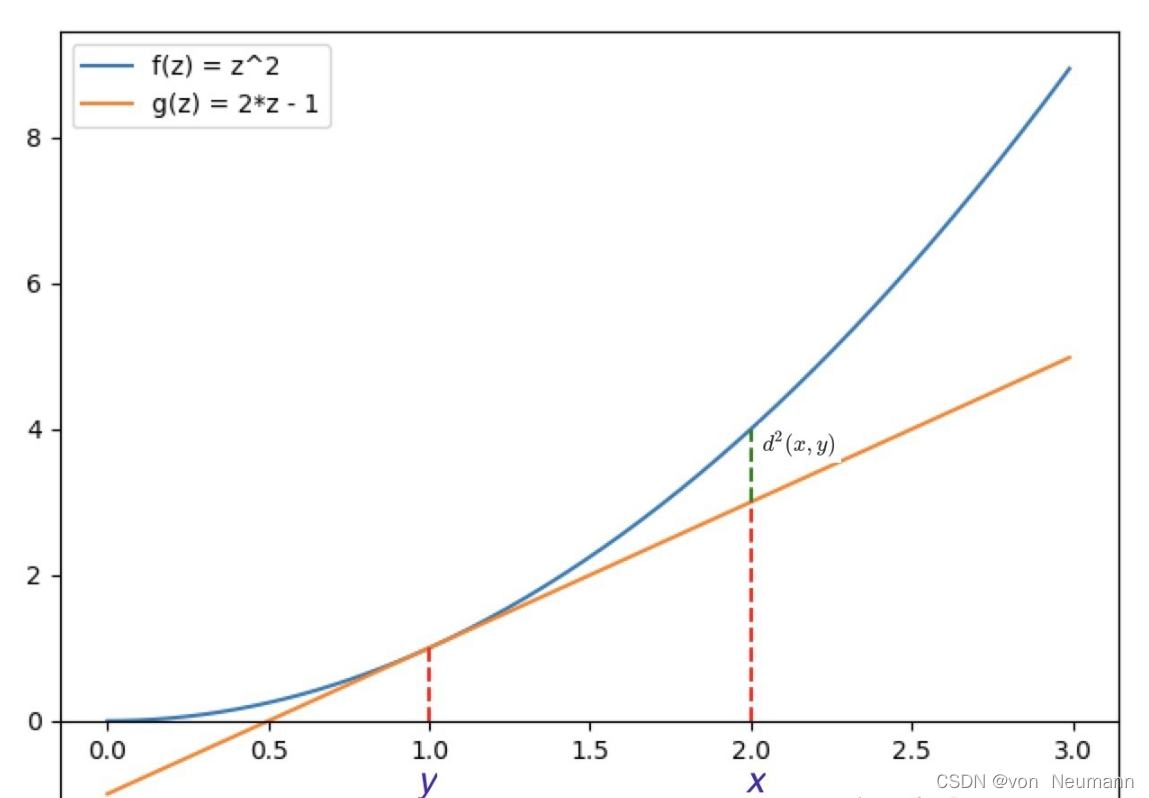
x处的取值。所以均方欧几里得距离的几何描述便是欧式模函数在点
x
x
x和其在
y
y
y点切线在点估计的差。如下图绿线所示:
那么一个很自然的想法就是把这个定义拓展,即对任意
R
n
R^n
Rn的函数
f
(
x
)
f(x)
f(x),我们都可以定义:
d
(
x
,
y
)
=
f
(
x
)
−
(
f
(
y
)
+
<
∇
f
(
y
)
,
x
−
y
>
)
d(x, y)=f(x)-(f(y)+<\nabla f(y), x-y>)
d(x,y)=f(x)−(f(y)+<∇f(y),x−y>)
若 f ( x ) f(x) f(x)是凸函数,则可以保证 d ( x , y ) ≥ 0 d(x, y)\geq0 d(x,y)≥0,上式也是Bregman散度(Bregman Divergence)的定义。
和F-散度类似,Bregman散度也是一大类散度的通用表达形式,具体的,根据
f
(
x
)
f(x)
f(x)取不同的函数,它可以表示不同的散度,其中KL散度也是它的一个特例:
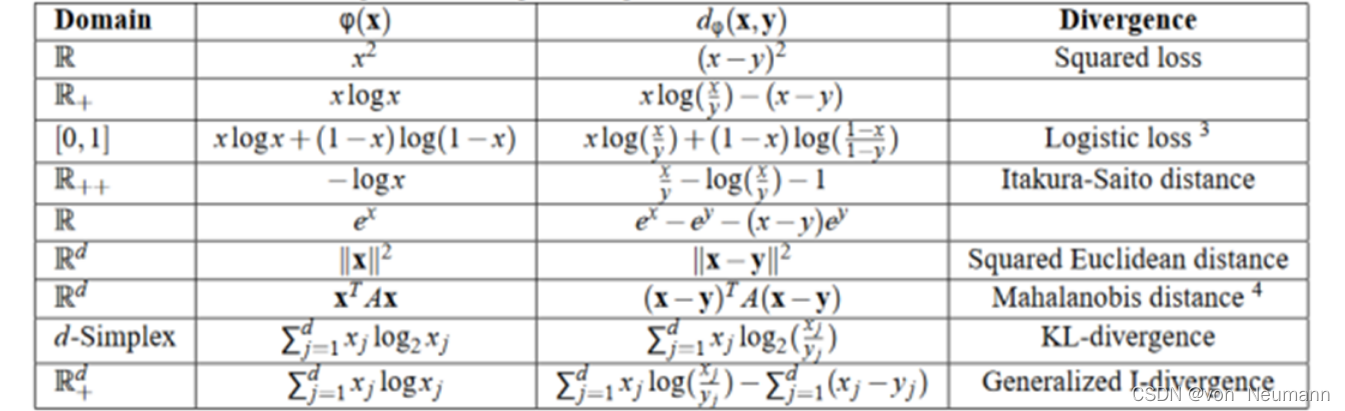























 8716
8716











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










