Java 递归和非递归实现二叉树的前序、中序、后序遍历

二叉树的遍历是非常重要的基础算法，今天闲来无事，对二叉树的前序、中序、后序遍历使用递归和非递归进行了一个实现。

 构造一个有9个节点的二叉树，如下

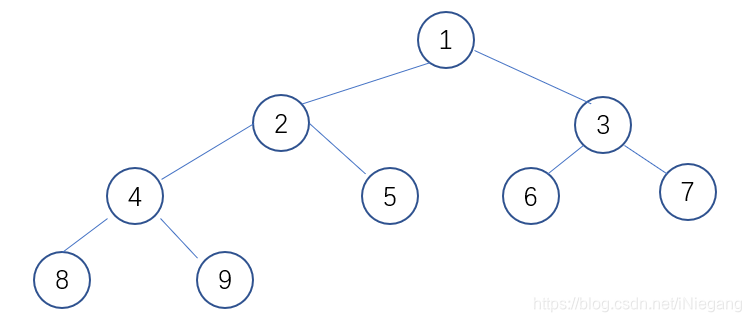
具体代码实现如下

public class BinaryTree {

    private static class Tree {
        private Integer value;

        private Tree leftNode;

        private Tree rightNode;
    }

    public static void main(String[] args) {
        Tree tree = new Tree();
        createTree(1, tree);
        List<Integer> rootFirstRecursiveResult = new ArrayList<>();
        rootFirstRecursive(rootFirstRecursiveResult, tree);
        System.out.println("Root First By Recursive: " + rootFirstRecursiveResult);
        System.out.println("Root First By not Recursive: " + rootFirstNotRecursive(tree));

        List<Integer> rootMiddleRecursiveResult = new ArrayList<>();
        rootMiddleRecursive(rootMiddleRecursiveResult, tree);
        System.out.println("Root Middle By Recursive: " + rootMiddleRecursiveResult);
        System.out.println("Root Middle By not Recursive: " + rootMiddleNotRecursive(tree));

        List<Integer> rootLastRecursiveResult = new ArrayList<>();
        rootLastRecursive(rootLastRecursiveResult, tree);
        System.out.println("Root Last By Recursive: " + rootLastRecursiveResult);
        System.out.println("Root Last By not Recursive: " + rootLastNotRecursive(tree));
    }

    /**
     * 创建一棵二叉树，最大节点的值为9
     */
    private static void createTree(int value, Tree tree) {
        if (value > 9) {
            return;
        }
        tree.value = value;
        if (2 * value > 9) {
            return;
        }
        tree.leftNode = new Tree();
        tree.rightNode = new Tree();
        createTree(2 * tree.value, tree.leftNode);
        createTree(2 * tree.value + 1, tree.rightNode);
    }

    /**
     * 用递归实现先序遍历
     */
    private static void rootFirstRecursive(List<Integer> visited, Tree tree) {
        if (tree == null) {
            return;
        }
        visited.add(tree.value);
        rootFirstRecursive(visited, tree.leftNode);
        rootFirstRecursive(visited, tree.rightNode);
    }

    /**
     * 用非递归实现先序遍历
     * 思路：利用栈先进后出的特性，将当前节点的右节点和左节点入栈，然后依次弹出
     */
    private static List<Integer> rootFirstNotRecursive(Tree tree) {
        List<Integer> result = new ArrayList<>();
        Stack<Tree> stack = new Stack<>();
        stack.push(tree);
        while (!stack.isEmpty()) {
            tree = stack.pop();
            result.add(tree.value);
            if (tree.rightNode != null) {
                stack.push(tree.rightNode);
            }
            if (tree.leftNode != null) {
                stack.push(tree.leftNode);
            }
        }
        return result;
    }

    /**
     * 用递归实现中序遍历
     */
    private static void rootMiddleRecursive(List<Integer> visited, Tree tree) {
        if (tree == null) {
            return;
        }
        rootMiddleRecursive(visited, tree.leftNode);
        visited.add(tree.value);
        rootMiddleRecursive(visited, tree.rightNode);
    }

    /**
     * 用非递归实现中序遍历
     * 思路：利用栈先进后出的特性，首先找到其最左的节点，出栈，考虑到该节点可能有右子树，因此再考察其右子树
     */
    private static List<Integer> rootMiddleNotRecursive(Tree tree) {
        List<Integer> result = new ArrayList<>();
        Stack<Tree> stack = new Stack<>();
        while (!stack.isEmpty() || tree != null) {
            while (tree != null) {
                stack.push(tree);
                tree = tree.leftNode;
            }

            if (!stack.isEmpty()) {
                tree = stack.pop();
                result.add(tree.value);
                tree = tree.rightNode;
            }
        }
        return result;
    }

    /**
     * 用递归实现后序遍历
     */
    private static void rootLastRecursive(List<Integer> visited, Tree tree) {
        if (tree == null) {
            return;
        }
        rootLastRecursive(visited, tree.leftNode);
        rootLastRecursive(visited, tree.rightNode);
        visited.add(tree.value);
    }

    /**
     * 用非递归实现后序遍历
     * 思路：先序遍历是根左右，后序遍历是左右根，那如果把先序遍历的代码改造为根右左，并把遍历结果存入一个新的栈中，再利用栈的先进后出的特性，即可得到左右根的结果
     */
    private static List<Integer> rootLastNotRecursive(Tree tree) {
        List<Integer> result = new ArrayList<>();
        Stack<Tree> stack1 = new Stack<>();
        Stack<Tree> stack2 = new Stack<>();
        stack1.push(tree);
        while (!stack1.isEmpty()) {
            tree = stack1.pop();
            stack2.push(tree);
            if (tree.leftNode != null) {
                stack1.push(tree.leftNode);
            }
            if (tree.rightNode != null) {
                stack1.push(tree.rightNode);
            }
        }

        while (!stack2.isEmpty()) {
            result.add(stack2.pop().value);
        }
        return result;
    }
}