算法系列之三：妖怪与和尚过河问题

有三个和尚（或传教士）和三个妖怪（或食人怪）过河，只有一条能装下两个人（和尚或妖怪）的船，在河的任何一方或者船上，如果妖怪的人数大于和尚的人数，那么和尚就会有被吃掉的危险。你能不能找出一种安全的渡河方法呢？

        这是一个很有意思的智力题，但是并不难，每次可以选择一个人或者两个人过河，只要保证在河的任何一边的和尚数量总是大于或等于妖怪的数量即可。这里先给出一种过河方法：

 

两个妖怪先过河，一个妖怪回来；

再两个妖怪过河，一个妖怪回来；

两个和尚过河，一个妖怪和一个和尚回来；

两个和尚过河，一个妖怪回来；

两个妖怪过河，一个妖怪回来；

两个妖怪过河。

 

过河的方法其实不止这一种，本文给出了一种求解全部过河方法的算法程序，可以通过穷举（状态树搜索）的方法得到全部四种过河方法。

 解决问题的思路

          题目的初始条件是三个和尚和三个妖怪在河的一边（还有一条船），解决问题后的终止条件是三个和尚和三个妖怪安全地过到河的对岸，如果把任意时刻妖怪和和尚的位置看作一个“状态”，则解决问题就是找到一条从初始状态变换到终止状态的路径。从初始状态开始，每选择一批妖怪或和尚过河（移动一次小船），就会从原状态产生一个新的状态，如果以人类思维解决这个问题，每次都会选择最佳的妖怪与和尚组合过河，使得它们过河后生成的新状态更接近最终状态，不断重复上述过程，直到得到最终状态。

        用计算机解决妖怪与和尚过河问题的思路也是通过状态转换，找到一条从初始状态到结束状态的转换路径。计算机不会进行理性分析，不知道每次如何选择最佳的过河方式，但是计算机擅长快速计算且不知疲劳，既然不知道如何选择过河方式，那就干脆把所有的过河方式都尝试一遍，找出所有可能的结果，当然也就包括成功过河的结果。

        这个思路其实和《三只水桶等分水问题》的解法类似，从初始状态开始，通过构造特定的穷举算法，对解空间中的所有状态进行穷举，就得到一棵以初始状态为根的状态树。如果状态树上某个叶子节点是题目要求的最终状态，则从根节点到此叶子节点之间的所有状态节点就是一个过河问题的解决过程。

状态的数学模型

        本节探讨一下如何建立状态的数学模型。题目要求并不强调三个妖怪之间或三个和尚之间的差异，只是关注它们在和河两岸的数量，因此无需赋予和尚和妖怪过多的属性，只要用数值分别表示它们在和两岸的数量即可确定某个时刻的状态。除了和尚与妖怪的数量，还有一个很关键的因素也会影响到数学模型，那就是船的状态。例如某一时刻，本地河边有两个和尚和两个妖怪，对岸有一个和尚和一个妖怪，此时船在河这边和在河对岸就分别是两个完全不同的状态。和尚与妖怪的状态就是数值，船有两个状态，在本地河边（LOCAL）和在对岸（REMOTE），我们用一个五元组来表示某个时刻的过河状态：[本地和尚数，本地妖怪数， 对岸和尚数，对岸妖怪数，船的位置]。用五元组表示的初始状态就是[3, 3, 0, 0, LOCAL]，问题解决的过河状态是[0, 0, 3, 3, REMOTE]。用C/C++定义此状态模型如下：

28 struct ItemState 29 { 30     ...... 31     int local_monster; 32     int local_monk; 33     int remote_monster; 34     int remote_monk; 35     BoatLocation boat;/*LOCAL or REMOTE*/ 36     ...... 37 };

        本题的状态空间就是以[3, 3, 0, 0, LOCAL]为根的一棵状态树，如果某个叶子节点表示的状态是求解状态[0, 0, 3, 3, REMOTE]，则从根节点到此节点之间的直系关系节点，就是过河过程中的所有中间状态，将这些中间状态按照父子关系依次输出，就是一个求解过程。以本文开始给出的一个求解过程为例，其状态转换过程如下图所示：

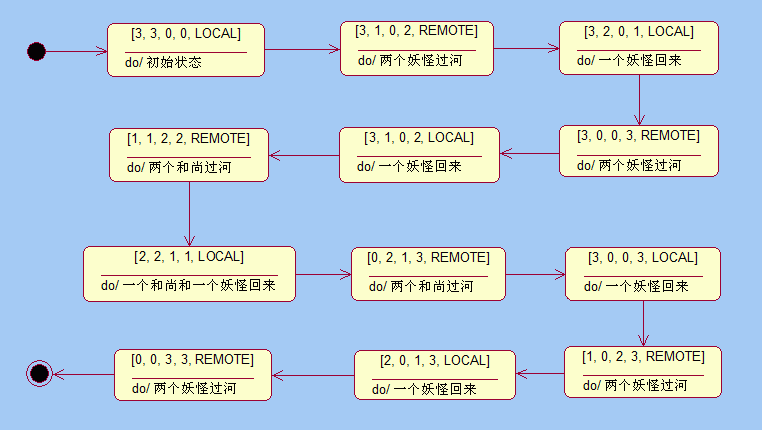
  图（1）一个求解的状态转换过程

        从一个状态转换到下一个状态，需要选择合适的和尚或妖怪组合完成一次过河动作，动作的概念在状态转换过程中扮演很重要的角色，如果不能明确的界定动作，随后的状态树搜索算法就无法实现。经过对本题的分析，求解算法需要10种过河动作，这10种动作分别是：

 

一个妖怪过河

两个妖怪过河

一个和尚过河

两个和尚过河

一个妖怪和一个和尚过河

一个妖怪返回

两个妖怪返回

一个和尚返回

两个和尚返回

一个妖怪和一个和尚返回

 

有了明确的动作的定义，最大的好处就是方便确定状态搜索过程中广度搜索的边界。算法中用ActionName标识10种动作，ActionName的C/C++定义如下：

12 enum ActionName 13 { 14     ONE_MONSTER_GO = 0, 15     TWO_MONSTER_GO, 16     ONE_MONK_GO, 17     TWO_MONK_GO, 18     ONE_MONSTER_ONE_MONK_GO, 19     ONE_MONSTER_BACK, 20     TWO_MONSTER_BACK, 21     ONE_MONK_BACK, 22     TWO_MONK_BACK, 23     ONE_MONSTER_ONE_MONK_BACK, 24     INVALID_ACTION_NAME, 25 };

 

状态树搜索算法

         状态树的搜索过程就是状态树的生成过程，本文介绍的算法采用的是深度优先遍历算法，每次遍历只暂时保存当前搜索的分支的所有状态，前面已经搜索过的状态是不保存的，只在必要的时候输出结果。因此，算法不需要复杂的树状数据结构保存整个状态树（也没有必要这么做），只需要一个队列能暂时存储当前搜索分支上的所有状态即可。这个队列初始时只有一个初始状态，随着搜索的进行逐步增加，当搜索算法完成后，队列中应该仍然只有一个初始状态。

        上一节已经分析过了，每个状态所能采用的过河动作只能是ActionName标识的10种动作中的一种（当然并不是每种动作都适用于此状态），有了这个动作范围，搜索状态树的穷举算法就非常简单了，只需将当前状态分别与这10种动作进行组合，就可以得到状态树上这个状态节点的若干个子节点，递归上述过程，就可以得到完整的状态树。图（2）即是深度优先搜索算法的流程图：

 

 

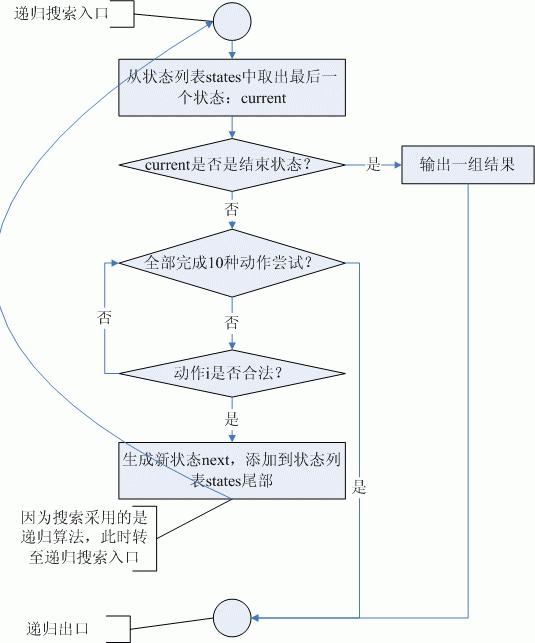
 图（2）状态树搜索算法流程图

 

算法相关的数据结构

        “状态树搜索算法”一节已经介绍过状态搜索的过程，在这个过程中使用了一个列表存放当前一次深度搜索所处理过的状态，这是一个辅助的数据组织方式，但是对算法实现很重要。考虑到算法每次都是从列表尾部取出当前状态，同时将新生成的状态插入到列表尾部，本文的算法采用std::deque来组织这个列表。这个列表将作为递归搜索的参数传递，算法开始时，将列表初始化为只有一个初始状态：

98     std::deque<ItemState> states;  99     ItemState init; 100  101     states.push_back(init);

        states中的状态是随着搜索过程有序添加的，从begin到end就是状态转换的完整过程。除此之外，states还用来避免算法陷入状态循环。每当生成一个新状态，都要判断一下新状态是否是states中已经处理过的状态，如果是则放弃当前新状态。相关的判断由IsProcessedState()函数实现：

27 bool IsProcessedState(std::deque<ItemState>& states, ItemState& newState) 28 { 29     std::deque<ItemState>::iterator it= states.end(); 30  31     it = find_if( states.begin(), states.end(), 32                   std::bind2nd(std::ptr_fun(IsSameItemState), newState) ); 33  34     return (it != states.end()); 35 }

         每当找到一个过河方法时，就需要打印过河过程，利用STL的便利，PrintResult()函数的实现也很简单：

37 void PrintResult(std::deque<ItemState>& states) 38 { 39     std::cout<< "Find Result : "<< std::endl; 40     for_each(states.begin(), states.end(), std::mem_fun_ref(&ItemState::PrintStates)); 41     std::cout<< std::endl << std::endl; 42 }

算法实现主要代码

        算法的核心是ProcessState()函数，ProcessState()函数通过对自身的递归调用实现对状态树的搜索，代码实现如下：

79 void ProcessState(std::deque<ItemState>& states) 80 { 81     ItemState current= states.back();/*每次都从当前状态开始*/ 82     if(current.IsFinalState()) 83     { 84         PrintResult(states); 85         return; 86     } 87  88     /*尝试用10种动作分别与当前状态组合*/ 89     for(int i = 0; i < sizeof(actEffect)/ sizeof(actEffect[0]); i++) 90     { 91         ProcessStateOnNewAction(states, current, actEffect[i]); 92     } 93 }

 81－86行的代码检查states中的最后一个状态current是否是完成状态，如果是则输出结果，如果不是则从89行开始用10种动作分别与current状态组合，尝试变换到一个新状态，ProcessStateOnNewAction()函数负责这种尝试：

64 void ProcessStateOnNewAction(std::deque<ItemState>& states, 65                              ItemState& current, ActionEffect& ae) 66 { 67     ItemState next; 68     if(MakeActionNewState(current, ae, next)) 69     { 70         if(next.IsValidState()&& !IsProcessedState(states, next)) 71         { 72             states.push_back(next); 73             ProcessState(states); 74             states.pop_back(); 75         } 76     } 77 }

 

        MakeActionNewState()尝试在当前状态current上应用ae描述的动作，如果ae对于current不是一个合法的动作，则返回false，如果ae对于current是一个合法的动作，则生成新动作next，并且返回true。ae对于current状态是不合法的情况有多种，比如ae描述的是两个和尚过河，但是current状态中河这边的和尚只有一个；再比如ae描述的是一个过河动作，但是current状态中的船的状态却是REMOTE等等。如果ae动作能够从current状态转换出新状态next，则要继续判断next是否是合法状态，以及next是否是一个已经处理过的状态（代码70行的if语句）。ItemState::IsValidState()函数根据题意检查是否在河两岸存在和尚个数少于妖怪个数的情况，如果存在则和尚会被妖怪吃掉，就不是一个合法状态。72－74行的代码完成深度优先搜索算法的递归部分，如果next是合法状态，则将next添加到states队列的尾部，然后对ProcessState()函数递归调用，完成后要将next状态从states队列尾部删除，这是个关键，保证对10种动作处理的广度搜索能够正常进行。

        还要介绍一下动作列表：actEffect，它影响到MakeActionNewState()函数。影响状态的动作有10种，如果能有一种合适的动作定义，可以大大简化MakeActionNewState()函数的实现。经过分析发现，每一种动作只会对已知状态产生两个方面的影响：一方面是影响河两岸和尚与妖怪的个数，令一方面是影响船的位置。为此我们给动作产生的影响定义了一个量化状态：

27 struct ActionEffect 28 { 29     ActionName act; 30     BoatLocation boat_to;//船移动的方向 31     int move_monster; //此次移动的妖怪数量 32     int move_monk; //此次移动的和尚数量 33 };

         move_monster和move_monk是相对量化值，以过河之前的状态为基准，把和尚或妖怪移动到对岸则为负值，从对岸移动回来则为正值。这样以来，所有的动作都可以量化统一，例如一个妖怪和一个和尚过河这个动作，就可以量化实现为：

 

{ ONE_MONSTER_ONE_MONK_GO ,   REMOTE, -1, -1 }

 

有了量化实现的动作列表actEffect，MakeActionNewState()函数的实现就是这么简单：

44 bool MakeActionNewState(const ItemState& curState, ActionEffect& ae, ItemState& newState) 45 { 46     if(curState.CanTakeAction(ae)) 47     { 48         newState = curState; 49         newState.local_monster += ae.move_monster; 50         newState.local_monk    += ae.move_monk; 51         newState.remote_monster-= ae.move_monster; 52         newState.remote_monk   -= ae.move_monk; 53         newState.boat   = ae.boat_to; 54         newState.curAct = ae.act; 55  56         return true; 57     } 58  59     return false; 60 }

 

        至此算法的核心代码都已经讲解完毕，运行程序，最终得到了四种过河动作，PrintResult()函数打印的结果如下：

 

Find Result 1:

Two monster go over river

One monster go back

Two monster go over river

One monster go back

Two monk go over river

One monster and one monk go back

Two monk go over river

One monster go back

Two monster go over river

One monster go back

Two monster go over river

 

 

Find Result 2:

Two monster go over river

One monster go back

Two monster go over river

One monster go back

Two monk go over river

One monster and one monk go back

Two monk go over river

One monster go back

Two monster go over river

One monk go back

One monster and one monk go over river

 

 

Find Result 3:

One monster and one monk go over river

One monk go back

Two monster go over river

One monster go back

Two monk go over river

One monster and one monk go back

Two monk go over river

One monster go back

Two monster go over river

One monster go back

Two monster go over river

 

 

Find Result 4:

One monster and one monk go over river

One monk go back

Two monster go over river

One monster go back

Two monk go over river

One monster and one monk go back

Two monk go over river

One monster go back

Two monster go over river

One monk go back

One monster and one monk go over river

有兴趣的朋友可以调整代码中的两个常量：

9 const int monster_count = 3; 10 const int monk_count    = 4;

看看4个和尚和3个妖怪的情况是否有解，还有5个和尚和4个妖怪的情况等等。理论上讲，和尚数量少于妖怪数量是无解的，程序运行的结果是否是这样呢？自己试试吧。

分享到：

转自     http://blog.csdn.net/orbit/article/details/6630461#comments