矩阵计算小程序源码

矩阵计算小程序源码
矩阵计算小程序，可以进行矩阵转置、矩阵加法、矩阵乘法、矩阵的逆计算，样式及效果如下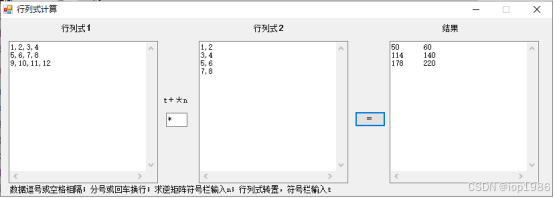： 矩阵加法计算

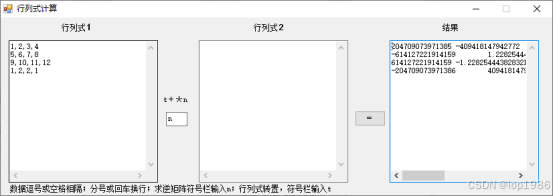
矩阵求逆
源码：

using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Text;
using System.Windows.Forms;
using diyMatrix;
namespace jzjs
{
    public partial class 行列式计算 : Form
    {
        public 行列式计算()
        {
            InitializeComponent();
        }

        private void button1_Click(object sender, EventArgs e)
        {
            Matrix mx1=new Matrix(), mx2=new Matrix(),mx3=new Matrix();
            if (fuhao.Text == "") { return; }
            switch (fuhao.Text[0])
            {
                case '+':
                    if (tiquM(ref mx1, textBox1.Text) == false) { return; }
                    if (tiquM(ref mx2, textBox2.Text) == false) { return; }
                    mx3 = Matrix.Add(mx1, mx2);
                    break;
                case '*':
                    if (tiquM(ref mx1, textBox1.Text) == false) { return; }
                    if (tiquM(ref mx2, textBox2.Text) == false) { return; }
                    mx3 = Matrix.Mutiply(mx1, mx2);
                    break;
                case 't':
                    if (tiquM(ref mx1, textBox1.Text) == false) { return; }
                    mx3 = mx1.Transpose();
                    break;
                case 'n':
                    //if (textBox1.Text == "") { return; }
                    if (tiquM(ref mx1, textBox1.Text) == false) { return; }
                    mx3 = Matrix.Inverse(mx1);
                    break;
                default:
                    return;
            }
            dis(mx3);

        }
        public Boolean tiquM(ref Matrix mx,String str)
        {
            String[] Arr1, Arr2;
            Arr1 = str.Split(new String[] { "\r\n", ";" }, StringSplitOptions.RemoveEmptyEntries);
            if (Arr1.Length==0) { return false; }
            Arr2 = Arr1[0].Split(new Char[] { ',','\t',' '}, StringSplitOptions.RemoveEmptyEntries);
            mx = new Matrix(Arr1.Length, Arr2.Length);
            for (int i = 0; i < Arr1.Length; i++)
            {
                Arr2 = null;
                Arr2 = Arr1[i].Split(new Char[] { ',', '\t', ' ' }, StringSplitOptions.RemoveEmptyEntries);
                for (int j = 0; j < Arr2.Length; j++)
                {
                    mx.SetNum(i, j, Convert.ToDouble(Arr2[j]));
                }
            }
            return true;

        }
        public void dis(Matrix mx)
        {
            for (int i = 0; i < mx.row; i++)
            {
                for (int j = 0; j < mx.col; j++)
                {
                    if (j != 0) { textBox3.AppendText("\t"); }
                    textBox3.AppendText(mx.getNum(i, j).ToString());
                }
                textBox3.AppendText("\r\n");
            }
        }



    }
}
using System;
namespace diyMatrix
{
    public class Matrix
    {
        double[,] matrix;
        public int row = 0, col = 0;
        //int i=0,j=0;
        //int count=1;
        //定义三个不同情况下的构造函数
        public Matrix()
        {
        }
        public Matrix(int row)
        {
            matrix = new double[row, row];
        }
        public Matrix(int row, int col)
        {
            this.row = row;
            this.col = col;
            matrix = new double[row, col];
        }
        //复制构造函数
        public Matrix(Matrix m)
        {
            int row = m.row;
            int col = m.col;
            matrix = new double[row, col];
            for (int i = 0; i < row; i++)
                for (int j = 0; j < col; j++)
                    matrix[i, j] = m.getNum(i, j);
        }
        //输入相应的值，对矩阵进行设置
        public void SetNum(int i, int j, double num)
        {
            matrix[i, j] = num;
        }
        //得到相应的矩阵某个数
        public double getNum(int i, int j)
        {
            return matrix[i, j];
        }
        /*  //输出矩阵
          public void OutputM()
          {
              Console.WriteLine("矩阵为：");
              for (int p = 0; p < row; p++)
              {
                  for (int q = 0; q < col; q++)
                  {
                      Console.Write("\t" + matrix[p, q]);
                  }
                  Console.Write("\n");
              }
          }
          //输入矩阵具体数字实现
          public void InputM(int Row, int Col)
          {
              for (int a = 0; a < Col; a++)
              {
                  for (int b = 0; b < Col; b++)
                  {
                      Console.WriteLine("第{0}行，第{1}列", a + 1, b + 1);
                      double value = Convert.ToDouble(Console.ReadLine());
                      this.SetNum(a, b, value);
                  }
              }
          }
          */
        //输入矩阵具体数字实现
        //得到、设置matrix
        public double[,] Detail
        {
            get { return matrix; }
            set
            {
                matrix = value;
                row = matrix.GetLength(0);
                col = matrix.GetLength(1);
            }
        }
        //矩阵转置实现
        public Matrix Transpose()
        {
            Matrix another = new Matrix(col, row);
            for (int i = 0; i < row; i++)
            {
                for (int j = 0; j < col; j++)
                {
                    another.SetNum(j, i, matrix[i, j]);
                }
            }
            return another;
        }
        //矩阵相加实现
        public static Matrix Add(Matrix lm, Matrix rm)
        {
            //行出错
            if (lm.row != rm.row)
            {
                System.Exception e = new Exception("相加的两个矩阵的行数不等");
                throw e;
            }
            //列出错
            if (lm.col != rm.col)
            {
                System.Exception e = new Exception("相加的两个矩阵的列数不等");
                throw e;
            }
            Matrix another = new Matrix(lm.row, lm.col);
            for (int i = 0; i < lm.row; i++)
            {
                for (int j = 0; j < lm.col; j++)
                {
                    double temp = lm.getNum(i, j) + rm.getNum(i, j);
                    another.SetNum(i, j, temp);
                }
            }
            return another;
        }
        //矩阵相乘实现
        public static Matrix Mutiply(Matrix m1, Matrix m2)
        {
            double temp = 0;
            Matrix ret;
            if (m1.col != m2.row)
            {
                System.Exception e = new Exception("前者列数不等于后者行数，无法相乘");
                throw e;
            }
            ret = new Matrix(m1.row, m2.col);

            for (int i = 0; i < m1.row; i++)
            {
                for (int j = 0; j < m2.col; j++)
                {
                    for (int p = 0; p < m1.col; p++)
                    {
                        temp += m1.getNum(i, p) * m2.getNum(p, j);

                    }
                    ret.SetNum(i, j, temp);
                    temp = 0;
                }
            }
            return ret;
        }


        //矩阵求逆实现
        public static Matrix Inverse(Matrix M)
        {
            int m = M.row;
            int n = M.col;
            if (m != n)
            {
                Exception myException = new Exception("求逆的矩阵不是方阵");
                throw myException;
            }
            Matrix ret = new Matrix(m, n);
            double[,] a0 = M.Detail;
            double[,] a = (double[,])a0.Clone();
            double[,] b = ret.Detail;

            int i, j, row, k;
            double max, temp;

            //单位矩阵
            for (i = 0; i < n; i++)
            {
                b[i, i] = 1;
            }
            for (k = 0; k < n; k++)
            {
                max = 0; row = k;
                //找最大元，其所在行为row
                for (i = k; i < n; i++)
                {
                    temp = Math.Abs(a[i, k]);
                    if (max < temp)
                    {
                        max = temp;
                        row = i;
                    }

                }
                if (max == 0)
                {
                    Exception myException = new Exception("该矩阵无逆矩阵");
                    throw myException;
                }
                //交换k与row行
                if (row != k)
                {
                    for (j = 0; j < n; j++)
                    {
                        temp = a[row, j];
                        a[row, j] = a[k, j];
                        a[k, j] = temp;

                        temp = b[row, j];
                        b[row, j] = b[k, j];
                        b[k, j] = temp;
                    }

                }

                //首元化为1
                for (j = k + 1; j < n; j++) a[k, j] /= a[k, k];
                for (j = 0; j < n; j++) b[k, j] /= a[k, k];

                a[k, k] = 1;

                //k列化为0
                //对a
                for (j = k + 1; j < n; j++)
                {
                    for (i = 0; i < k; i++) a[i, j] -= a[i, k] * a[k, j];
                    for (i = k + 1; i < n; i++) a[i, j] -= a[i, k] * a[k, j];
                }
                //对b
                for (j = 0; j < n; j++)
                {
                    for (i = 0; i < k; i++) b[i, j] -= a[i, k] * b[k, j];
                    for (i = k + 1; i < n; i++) b[i, j] -= a[i, k] * b[k, j];
                }
                for (i = 0; i < n; i++) a[i, k] = 0;
                a[k, k] = 1;
            }

            return ret;
        }



    }
}