傅里叶变换快速入门

傅里叶变换快速入门

本文记录自己学习理解图像傅里叶变换的过程

非常值得读的文章：傅里叶分析之掐死教程 --》https://zhuanlan.zhihu.com/p/19763358

傅里叶变换/级数的作用

• 傅里叶的一个牛B发现：任何周期函数都可以看作不同振幅，不同相位正弦波的叠加。

• 傅里叶变换/级数的作用就是：将一个周期函数分解，得到诸多正弦波。

• 记录一个正弦波只需知道其振幅、频率和相位即可。这样我们就可以得到相位谱和幅频谱。

• 傅里叶级数就是将一个周期函数分解成诸多离散的正弦波加和；

• 傅里叶变换能将所有函数分解成连续的正弦波加和。

一维正弦波傅里叶变换实现

• 实现过程大致是：在一定区间里进行采样得到x点列表，通过sin函数得到y点列表，再使用快速傅里叶变换(FFT)。

• 一般科学工具包里都是使用FFT的，FFT是基于离散傅里叶变换(DFT)的升级版。

• DFT理解好文–》https://www.zhihu.com/question/21314374/answer/542909849

• 为什么计算机里会使用DFT的思想呢？一维我们没法将一个连续函数进行傅里叶变换，只能在一个函数上进行点采样进行傅里叶变换。

代码如下：

# FFT作用于正弦信号
import numpy as np
import matplotlib.pyplot as plt

# 采样点数
Fs = 250                    
# 生成x，在0-1上生成300个点 
x = np.linspace(0, 1, Fs)

# sin(2pi * ff * x)，频率ff1
ff1 = 10;      
y1 = np.cos(2 * np.pi * ff1 * x)
# 该函数周期为 2pi / 2ff pi; 即 T = 0.1 所以频率 f = 10 = ff1
ff2 = 20
y2 = 2 * np.cos(2 * np.pi * ff2 * x)

y = y1 + y2

frq = np.arange(Fs)  

# 需要对傅里叶变换的结果取abs才能画图
YY = abs(np.fft.fft(y)) 

# 看了FFT后可以理解该公式。强度需除以 n/2
YY_norm = YY/Fs * 2

plt.figure(figsize=(7, 7))

plt.subplot(211)
plt.xlabel("Amplitude")
plt.ylabel("Time")
plt.plot(x,y)

plt.subplot(212)
plt.xlabel("Frequency")
plt.ylabel("|Y|")
plt.plot(frq, YY_norm)

plt.show()

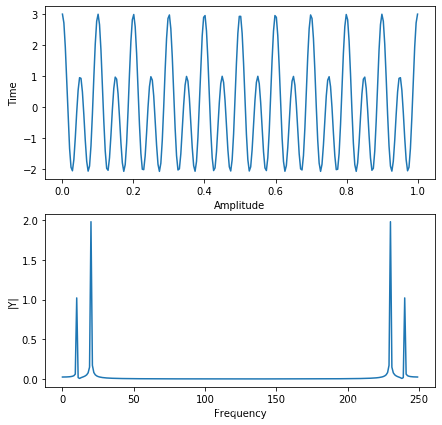
上文代码中我们对FFT变换的结果取了abs，这是因为傅里叶变换后的结果是个复数，复数部分就是相位造成的，上文中的DFT中有解释。

• 了解傅里叶变换公式后就会明白正弦波对应到频谱上都是一对对的出现的，呈现轴对称的姿态，所以一般仅看一半即可。上图中，中央是高频部分，两侧是低频部分。

• 以上就是从时域转换到频域。

• 上述中幅频谱的值又被称作傅里叶系数。

二维图像傅里叶变换

• 如果说一个波是由任意正弦波的叠加好理解，那么为什么任意图像也可以是波的叠加呢？

理解图像傅里叶变换频谱图的好文 --》 https://blog.csdn.net/viatorsun/article/details/82387854

• 直观理解：将图片灰度化之后，图片中的一列就可以用诸多正弦波来叠加拟合。

• 而事实上图像傅里叶变化正是用二维的正弦波进行叠加的。

二维正弦图像示意图 Z = sin(0.5x + y)

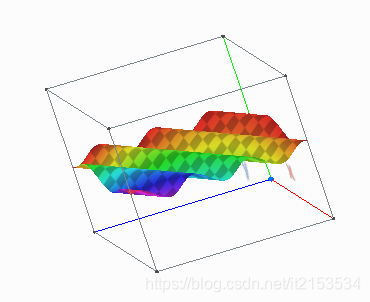
其他博客常见的黑白条纹图可以当做俯视图来看，波峰对应较高像素值，波谷对应较低像素值。

图像傅里叶变换实现

import cv2
import numpy as np
import matplotlib.pyplot as plt

img = cv2.imread('test3.jpg', 0) # 直接读为灰度图像
f = np.fft.fft2(img)             # 傅里叶变换
fshift = np.fft.fftshift(f)      # 频谱中心化

plt.figure(figsize=(10, 10))
s1 = np.log(np.abs(fshift))  #取绝对值：将复数变化成实数取对数的目的为了将数据变化到0-255
plt.subplot(121)
plt.imshow(img, 'gray')
plt.set
plt.title('original')

plt.subplot(122)
plt.imshow(s1,'gray')
plt.title('center')

plt.show()

• 上图中频谱是经过中心化的：是中心对称的，不是轴对称。中央是低频部分，两侧是高频部分。

• 上图就是从空域转化为频域。