简介
Matrix ,中文里叫矩阵,高等数学里有介绍。Android中的Matrix类是一个3x3的位置坐标矩阵,在图像处理方面,主要是用于平面的缩放、平移、旋转等操作。
Matrix的数学原理
首先了解下这个3 x 3的矩阵,其内容如下所示:
Matrix的对图像的处理可分为四类基本变换:
| 英文 | 中文 |
|---|---|
| Translate | 平移变换 |
| Rotate | 旋转变换 |
| Scale | 缩放变换 |
| Skew | 错切变换 |
从字面上理解,矩阵中的MSCALE用于处理缩放变换,MSKEW用于处理错切变换,MTRANS用于处理平移变换,MPERSP用于处理透视变换。实际中当然不能完全按照字面上的说法去理解Matrix。同时,在Android的文档中,未见到用Matrix进行透视变换的相关说明,所以本文也不讨论这方面的问题。
针对每种变换,Android提供了pre、set和post三种操作方式。其中:
- set用于设置Matrix中的值。
- pre是先乘,因为矩阵的乘法不满足交换律,因此先乘、后乘必须要严格区分。先乘相当于矩阵运算中的右乘。
- post是后乘,因为矩阵的乘法不满足交换律,因此先乘、后乘必须要严格区分。后乘相当于矩阵运算中的左乘。
除平移变换(Translate)外,旋转变换(Rotate)、缩放变换(Scale)和错切变换(Skew)都可以围绕一个中心点来进行,如果不指定,在默认情况下是围绕(0, 0)来进行相应的变换的。
下面我们来看看四种变换的具体情形。由于所有的图形都是有点组成,因此我们只需要考察一个点相关变换即可。
平移变换
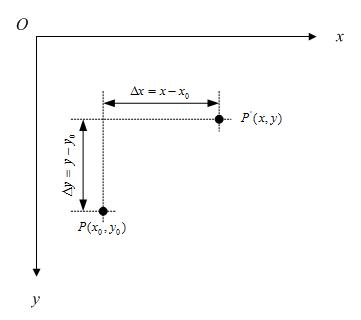
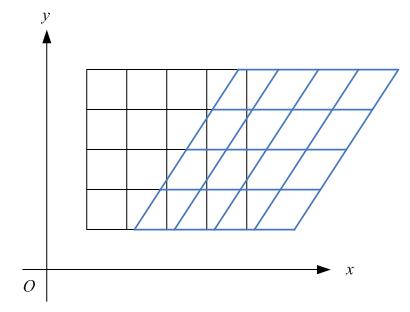
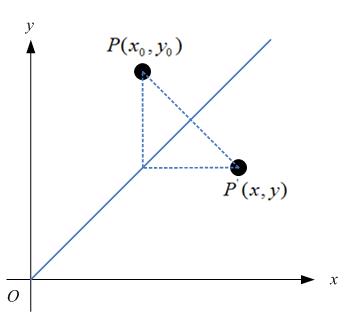
假定有一个点的坐标是 <nobr><span class="math" id="MathJax-Span-1" style="width: 3.883em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.718em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.032em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-2"><span class="msubsup" id="MathJax-Span-3"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.719em, 1000em, 2.756em, -0.577em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-4" style="font-family: STIXGeneral-Italic;">P</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.641em;"><span class="mo" id="MathJax-Span-5" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">(</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-6"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-7" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-8" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-9" style="font-family: STIXGeneral-Regular;">,</span><span class="msubsup" id="MathJax-Span-10" style="padding-left: 0.188em;"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-11" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-12" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-13" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.123em; vertical-align: -0.353em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-1">P_(x_0,y_0)</script><nobr><span class="math" id="MathJax-Span-14" style="width: 6.017em; display: inline-block;"><span style="display: inline-block; position: relative; width: 5.769em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.508em, 1000em, 2.892em, -0.577em); top: -2.5em; left: 0em;"><span class="mrow" id="MathJax-Span-15"><span class="texatom" id="MathJax-Span-16"><span class="mrow" id="MathJax-Span-17"><span class="mo" id="MathJax-Span-18"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">,</span></span></span></span><span class="texatom" id="MathJax-Span-19"><span class="mrow" id="MathJax-Span-20"><span class="mo" id="MathJax-Span-21"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">将</span></span></span></span><span class="texatom" id="MathJax-Span-22"><span class="mrow" id="MathJax-Span-23"><span class="mo" id="MathJax-Span-24"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">其</span></span></span></span><span class="texatom" id="MathJax-Span-25"><span class="mrow" id="MathJax-Span-26"><span class="mo" id="MathJax-Span-27"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">移</span></span></span></span><span class="texatom" id="MathJax-Span-28"><span class="mrow" id="MathJax-Span-29"><span class="mo" id="MathJax-Span-30"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">动</span></span></span></span><span class="texatom" id="MathJax-Span-31"><span class="mrow" id="MathJax-Span-32"><span class="mo" id="MathJax-Span-33"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">到</span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.5em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.173em; vertical-align: -0.275em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-2"> ,将其移动到 </script><nobr><span class="math" id="MathJax-Span-34" style="width: 2.817em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.692em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.032em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-35"><span class="msubsup" id="MathJax-Span-36"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.719em, 1000em, 2.756em, -0.577em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-37" style="font-family: STIXGeneral-Italic;">P</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.641em;"><span class="mo" id="MathJax-Span-38" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">(</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mi" id="MathJax-Span-39" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-40" style="font-family: STIXGeneral-Regular;">,</span><span class="mi" id="MathJax-Span-41" style="font-family: STIXGeneral-Italic; padding-left: 0.188em;">y</span><span class="mo" id="MathJax-Span-42" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.123em; vertical-align: -0.353em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-3">P_(x,y)</script> ,再假定在x轴和y轴方向移动的大小分别为:
△x = <nobr><span class="math" id="MathJax-Span-43" style="width: 2.283em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.179em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-44"><span class="mi" id="MathJax-Span-45" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mtext" id="MathJax-Span-46" style="font-family: STIXGeneral-Regular;"></span><span class="mo" id="MathJax-Span-47" style="font-family: STIXGeneral-Regular; padding-left: 0.25em;">−</span><span class="mtext" id="MathJax-Span-48" style="font-family: STIXGeneral-Regular; padding-left: 0.25em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.603em; vertical-align: -0.078em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-4">x \ - \ </script><nobr><span class="math" id="MathJax-Span-49" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.532em, -0.604em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-50"><span class="msubsup" id="MathJax-Span-51"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-52" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-53" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.758em; vertical-align: -0.233em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-5">x_0</script>
△y = <nobr><span class="math" id="MathJax-Span-54" style="width: 2.283em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.179em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-55"><span class="mi" id="MathJax-Span-56" style="font-family: STIXGeneral-Italic;">y</span><span class="mtext" id="MathJax-Span-57" style="font-family: STIXGeneral-Regular;"></span><span class="mo" id="MathJax-Span-58" style="font-family: STIXGeneral-Regular; padding-left: 0.25em;">−</span><span class="mtext" id="MathJax-Span-59" style="font-family: STIXGeneral-Regular; padding-left: 0.25em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.806em; vertical-align: -0.281em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-6">y \ - \ </script><nobr><span class="math" id="MathJax-Span-60" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.623em, -0.601em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-61"><span class="msubsup" id="MathJax-Span-62"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-63" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-64" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.853em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-7">y_0</script>
如下图所示:
不难知道:
<nobr><span class="math" id="MathJax-Span-65" style="width: 2.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-66"><span class="mi" id="MathJax-Span-67" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-68" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-69" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.603em; vertical-align: -0.078em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-8">x = \ </script><nobr><span class="math" id="MathJax-Span-70" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.532em, -0.604em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-71"><span class="msubsup" id="MathJax-Span-72"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-73" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-74" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.758em; vertical-align: -0.233em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-9">x_0</script> + △x
<nobr><span class="math" id="MathJax-Span-75" style="width: 2.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-76"><span class="mi" id="MathJax-Span-77" style="font-family: STIXGeneral-Italic;">y</span><span class="mo" id="MathJax-Span-78" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-79" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.806em; vertical-align: -0.281em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-10">y = \ </script><nobr><span class="math" id="MathJax-Span-80" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.623em, -0.601em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-81"><span class="msubsup" id="MathJax-Span-82"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-83" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-84" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.853em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-11">y_0</script> + △y
如果用矩阵来表示的话,就可以写成:
旋转变换
围绕坐标原点旋转
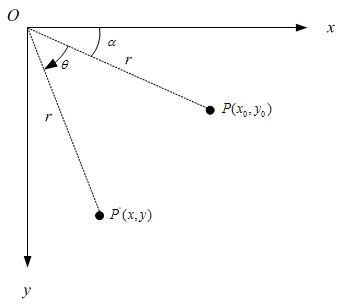
假定有一个点的坐标是 <nobr><span class="math" id="MathJax-Span-85" style="width: 3.883em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.718em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.032em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-86"><span class="msubsup" id="MathJax-Span-87"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.719em, 1000em, 2.756em, -0.577em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-88" style="font-family: STIXGeneral-Italic;">P</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.641em;"><span class="mo" id="MathJax-Span-89" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">(</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-90"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-91" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-92" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-93" style="font-family: STIXGeneral-Regular;">,</span><span class="msubsup" id="MathJax-Span-94" style="padding-left: 0.188em;"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-95" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-96" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-97" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.123em; vertical-align: -0.353em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-12">P_(x_0,y_0)</script><nobr><span class="math" id="MathJax-Span-98" style="width: 12.55em; display: inline-block;"><span style="display: inline-block; position: relative; width: 12.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.572em, 1000em, 2.956em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-99"><span class="texatom" id="MathJax-Span-100"><span class="mrow" id="MathJax-Span-101"><span class="mo" id="MathJax-Span-102"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">,</span></span></span></span><span class="texatom" id="MathJax-Span-103"><span class="mrow" id="MathJax-Span-104"><span class="mo" id="MathJax-Span-105"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">相</span></span></span></span><span class="texatom" id="MathJax-Span-106"><span class="mrow" id="MathJax-Span-107"><span class="mo" id="MathJax-Span-108"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">对</span></span></span></span><span class="texatom" id="MathJax-Span-109"><span class="mrow" id="MathJax-Span-110"><span class="mo" id="MathJax-Span-111"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">坐</span></span></span></span><span class="texatom" id="MathJax-Span-112"><span class="mrow" id="MathJax-Span-113"><span class="mo" id="MathJax-Span-114"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">标</span></span></span></span><span class="texatom" id="MathJax-Span-115"><span class="mrow" id="MathJax-Span-116"><span class="mo" id="MathJax-Span-117"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">原</span></span></span></span><span class="texatom" id="MathJax-Span-118"><span class="mrow" id="MathJax-Span-119"><span class="mo" id="MathJax-Span-120"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">点</span></span></span></span><span class="texatom" id="MathJax-Span-121"><span class="mrow" id="MathJax-Span-122"><span class="mo" id="MathJax-Span-123"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">顺</span></span></span></span><span class="texatom" id="MathJax-Span-124"><span class="mrow" id="MathJax-Span-125"><span class="mo" id="MathJax-Span-126"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">时</span></span></span></span><span class="texatom" id="MathJax-Span-127"><span class="mrow" id="MathJax-Span-128"><span class="mo" id="MathJax-Span-129"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">针</span></span></span></span><span class="texatom" id="MathJax-Span-130"><span class="mrow" id="MathJax-Span-131"><span class="mo" id="MathJax-Span-132"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">旋</span></span></span></span><span class="texatom" id="MathJax-Span-133"><span class="mrow" id="MathJax-Span-134"><span class="mo" id="MathJax-Span-135"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">转</span></span></span></span><span class="mi" id="MathJax-Span-136" style="font-family: STIXGeneral-Italic;">θ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.014em;"></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.173em; vertical-align: -0.275em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-13"> ,相对坐标原点顺时针旋转 \theta</script>后的情形,同时假定P点离坐标原点的距离为r,如下图:
那么,
如果用矩阵,就可以表示为:
围绕某个点旋转
如果是围绕某个点 <nobr><span class="math" id="MathJax-Span-137" style="width: 3.217em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.077em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.143em, -0.529em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-138"><span class="mo" id="MathJax-Span-139" style="font-family: STIXGeneral-Regular;">(</span><span class="msubsup" id="MathJax-Span-140"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-141" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mi" id="MathJax-Span-142" style="font-size: 70.7%; font-family: STIXGeneral-Italic;">p</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-143" style="font-family: STIXGeneral-Regular;">,</span><span class="msubsup" id="MathJax-Span-144" style="padding-left: 0.188em;"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-145" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mi" id="MathJax-Span-146" style="font-size: 70.7%; font-family: STIXGeneral-Italic;">p</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-147" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.238em; vertical-align: -0.468em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-14">(x_p,y_p)</script><nobr><span class="math" id="MathJax-Span-148" style="width: 5.55em; display: inline-block;"><span style="display: inline-block; position: relative; width: 5.321em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.572em, 1000em, 2.956em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-149"><span class="texatom" id="MathJax-Span-150"><span class="mrow" id="MathJax-Span-151"><span class="mo" id="MathJax-Span-152"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">顺</span></span></span></span><span class="texatom" id="MathJax-Span-153"><span class="mrow" id="MathJax-Span-154"><span class="mo" id="MathJax-Span-155"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">时</span></span></span></span><span class="texatom" id="MathJax-Span-156"><span class="mrow" id="MathJax-Span-157"><span class="mo" id="MathJax-Span-158"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">针</span></span></span></span><span class="texatom" id="MathJax-Span-159"><span class="mrow" id="MathJax-Span-160"><span class="mo" id="MathJax-Span-161"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">旋</span></span></span></span><span class="texatom" id="MathJax-Span-162"><span class="mrow" id="MathJax-Span-163"><span class="mo" id="MathJax-Span-164"><span style="font-family: STIXGeneral, 'Arial Unicode MS', serif; font-size: 96%; font-style: normal; font-weight: normal;">转</span></span></span></span><span class="mi" id="MathJax-Span-165" style="font-family: STIXGeneral-Italic;">θ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.014em;"></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.173em; vertical-align: -0.275em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-15"> 顺时针旋转 \theta</script> ,那么用矩阵表示为:
可以化为:
很显然:
- 如下图所示,是将坐标原点移动到点 <nobr><span class="math" id="MathJax-Span-166" style="width: 3.217em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.077em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.143em, -0.529em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-167"><span class="mo" id="MathJax-Span-168" style="font-family: STIXGeneral-Regular;">(</span><span class="msubsup" id="MathJax-Span-169"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-170" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mi" id="MathJax-Span-171" style="font-size: 70.7%; font-family: STIXGeneral-Italic;">p</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-172" style="font-family: STIXGeneral-Regular;">,</span><span class="msubsup" id="MathJax-Span-173" style="padding-left: 0.188em;"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-174" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mi" id="MathJax-Span-175" style="font-size: 70.7%; font-family: STIXGeneral-Italic;">p</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-176" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.238em; vertical-align: -0.468em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-16">(x_p,y_p)</script> 后, <nobr><span class="math" id="MathJax-Span-177" style="width: 3.883em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.718em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.032em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-178"><span class="msubsup" id="MathJax-Span-179"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.719em, 1000em, 2.756em, -0.577em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-180" style="font-family: STIXGeneral-Italic;">P</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.641em;"><span class="mo" id="MathJax-Span-181" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">(</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-182"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-183" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-184" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-185" style="font-family: STIXGeneral-Regular;">,</span><span class="msubsup" id="MathJax-Span-186" style="padding-left: 0.188em;"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-187" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-188" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-189" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.123em; vertical-align: -0.353em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-17">P_(x_0,y_0)</script>的新坐标。
- 如下图所示,是将上一步变换后的 <nobr><span class="math" id="MathJax-Span-190" style="width: 3.883em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.718em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.032em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-191"><span class="msubsup" id="MathJax-Span-192"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.719em, 1000em, 2.756em, -0.577em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-193" style="font-family: STIXGeneral-Italic;">P</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.641em;"><span class="mo" id="MathJax-Span-194" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">(</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-195"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-196" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-197" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-198" style="font-family: STIXGeneral-Regular;">,</span><span class="msubsup" id="MathJax-Span-199" style="padding-left: 0.188em;"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-200" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-201" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-202" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.123em; vertical-align: -0.353em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-18">P_(x_0,y_0)</script>,围绕新的坐标原点顺时针旋转<nobr><span class="math" id="MathJax-Span-203" style="width: 0.55em; display: inline-block;"><span style="display: inline-block; position: relative; width: 0.513em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.694em, 1000em, 2.767em, -0.55em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-204"><span class="mi" id="MathJax-Span-205" style="font-family: STIXGeneral-Italic;">θ<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.014em;"></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.85em; vertical-align: -0.078em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-19"> \theta</script> 。
- 如下图所示,是经过上一步旋转变换后,再将坐标原点移回到原来的坐标原点。
所以,围绕某一点进行旋转变换,可以分成3个步骤,即首先将坐标原点移至该点,然后围绕新的坐标原点进行旋转变换,再然后将坐标原点移回到原先的坐标原点。
缩放变换
理论上而言,一个点是不存在什么缩放变换的,但考虑到所有图像都是由点组成,因此,如果图像在x轴和y轴方向分别放大k1和k2倍的话,那么图像中的所有点的x坐标和y坐标均会分别放大k1和k2倍,即:
<nobr><span class="math" id="MathJax-Span-206" style="width: 2.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-207"><span class="mi" id="MathJax-Span-208" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-209" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-210" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.603em; vertical-align: -0.078em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-20">x = \ </script><nobr><span class="math" id="MathJax-Span-211" style="width: 2.017em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.923em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.304em, 1000em, 2.532em, -0.563em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-212"><span class="msubsup" id="MathJax-Span-213"><span style="display: inline-block; position: relative; width: 0.955em; height: 0px;"><span style="position: absolute; clip: rect(1.689em, 1000em, 2.767em, -0.563em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-214" style="font-family: STIXGeneral-Italic;">k<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.017em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.496em;"><span class="mn" id="MathJax-Span-215" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">1</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-216"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-217" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-218" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.01em; vertical-align: -0.233em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-21">k_1x_0</script>
<nobr><span class="math" id="MathJax-Span-219" style="width: 2.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-220"><span class="mi" id="MathJax-Span-221" style="font-family: STIXGeneral-Italic;">y</span><span class="mo" id="MathJax-Span-222" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-223" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.806em; vertical-align: -0.281em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-22">y = \ </script><nobr><span class="math" id="MathJax-Span-224" style="width: 2.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.987em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.304em, 1000em, 2.623em, -0.563em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-225"><span class="msubsup" id="MathJax-Span-226"><span style="display: inline-block; position: relative; width: 0.955em; height: 0px;"><span style="position: absolute; clip: rect(1.689em, 1000em, 2.767em, -0.563em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-227" style="font-family: STIXGeneral-Italic;">k<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.017em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.496em;"><span class="mn" id="MathJax-Span-228" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">2</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-229"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-230" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-231" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.105em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-23">k_2y_0</script>
用矩阵表示就是:
缩放变换比较好理解,就不多说了。
错切变换
错切变换(skew)在数学上又称为Shear mapping(可译为“剪切变换”)或者Transvection(缩并),它是一种比较特殊的线性变换。错切变换的效果就是让所有点的x坐标(或者y坐标)保持不变,而对应的y坐标(或者x坐标)则按比例发生平移,且平移的大小和该点到x轴(或y轴)的垂直距离成正比。错切变换,属于等面积变换,即一个形状在错切变换的前后,其面积是相等的。
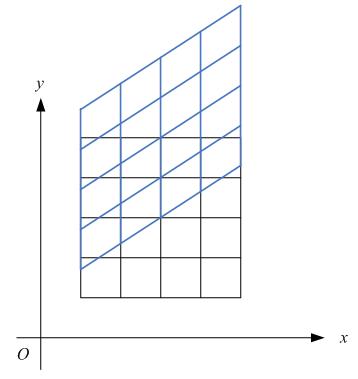
比如下图,各点的y坐标保持不变,但其x坐标则按比例发生了平移。这种情况将水平错切。
下图各点的x坐标保持不变,但其y坐标则按比例发生了平移。这种情况叫垂直错切。
假定一个点<nobr><span class="math" id="MathJax-Span-232" style="width: 3.883em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.718em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.032em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-233"><span class="msubsup" id="MathJax-Span-234"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.719em, 1000em, 2.756em, -0.577em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-235" style="font-family: STIXGeneral-Italic;">P</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.641em;"><span class="mo" id="MathJax-Span-236" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">(</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="msubsup" id="MathJax-Span-237"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-238" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-239" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-240" style="font-family: STIXGeneral-Regular;">,</span><span class="msubsup" id="MathJax-Span-241" style="padding-left: 0.188em;"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-242" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-243" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mo" id="MathJax-Span-244" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.123em; vertical-align: -0.353em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-24">P_(x_0,y_0)</script>经过错切变换后得到<nobr><span class="math" id="MathJax-Span-245" style="width: 2.817em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.692em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.696em, 1000em, 3.032em, -0.577em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-246"><span class="msubsup" id="MathJax-Span-247"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.719em, 1000em, 2.756em, -0.577em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-248" style="font-family: STIXGeneral-Italic;">P</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.641em;"><span class="mo" id="MathJax-Span-249" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">(</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span><span class="mi" id="MathJax-Span-250" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-251" style="font-family: STIXGeneral-Regular;">,</span><span class="mi" id="MathJax-Span-252" style="font-family: STIXGeneral-Italic; padding-left: 0.188em;">y</span><span class="mo" id="MathJax-Span-253" style="font-family: STIXGeneral-Regular;">)</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.123em; vertical-align: -0.353em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-25">P_(x,y)</script>,对于水平错切而言,应该有如下关系:
<nobr><span class="math" id="MathJax-Span-254" style="width: 3.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.013em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.916em, -0.604em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-255"><span class="mi" id="MathJax-Span-256" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-257" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-258" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span><span class="msubsup" id="MathJax-Span-259"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-260" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-261" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.758em; vertical-align: -0.233em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-26">x = \ x_0</script> + <nobr><span class="math" id="MathJax-Span-262" style="width: 1.55em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.474em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.689em, 1000em, 3.008em, -0.563em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-263"><span class="mi" id="MathJax-Span-264" style="font-family: STIXGeneral-Italic;">k<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.017em;"></span></span><span class="msubsup" id="MathJax-Span-265"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-266" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-267" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 1.105em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-27">ky_0</script>
<nobr><span class="math" id="MathJax-Span-268" style="width: 2.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-269"><span class="mi" id="MathJax-Span-270" style="font-family: STIXGeneral-Italic;">y</span><span class="mo" id="MathJax-Span-271" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-272" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.806em; vertical-align: -0.281em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-28">y = \ </script><nobr><span class="math" id="MathJax-Span-273" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.623em, -0.601em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-274"><span class="msubsup" id="MathJax-Span-275"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-276" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-277" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.853em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-29">y_0</script>
用矩阵表示就是:
扩展到3 x 3的矩阵就是下面这样的形式:
同理,对于垂直错切,可以有:
在数学上严格的错切变换就是上面这样的。在Android中除了有上面说到的情况外,还可以同时进行水平、垂直错切,那么形式上就是:
对称变换
除了上面讲到的4中基本变换外,事实上,我们还可以利用Matrix,进行对称变换。所谓对称变换,就是经过变化后的图像和原图像是关于某个对称轴是对称的。比如,某点 经过对称变换后得到,
如果对称轴是x轴,难么,
<nobr><span class="math" id="MathJax-Span-278" style="width: 3.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.013em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.916em, -0.604em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-279"><span class="mi" id="MathJax-Span-280" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-281" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-282" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span><span class="msubsup" id="MathJax-Span-283"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-284" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-285" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.758em; vertical-align: -0.233em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-30">x = \ x_0</script>
<nobr><span class="math" id="MathJax-Span-286" style="width: 3.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.013em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-287"><span class="mi" id="MathJax-Span-288" style="font-family: STIXGeneral-Italic;">y</span><span class="mo" id="MathJax-Span-289" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-290" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span><span class="mo" id="MathJax-Span-291" style="font-family: STIXGeneral-Regular; padding-left: 0.25em;">−</span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.806em; vertical-align: -0.281em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-31">y = \ -</script><nobr><span class="math" id="MathJax-Span-292" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.623em, -0.601em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-293"><span class="msubsup" id="MathJax-Span-294"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-295" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-296" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.853em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-32">y_0</script>
用矩阵表示就是:
如果对称轴是y轴,那么,
<nobr><span class="math" id="MathJax-Span-297" style="width: 4.417em; display: inline-block;"><span style="display: inline-block; position: relative; width: 4.231em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.916em, -0.604em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-298"><span class="mi" id="MathJax-Span-299" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-300" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-301" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span><span class="mo" id="MathJax-Span-302" style="font-family: STIXGeneral-Regular; padding-left: 0.25em;">−</span><span class="msubsup" id="MathJax-Span-303" style="padding-left: 0.25em;"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-304" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-305" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.758em; vertical-align: -0.233em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-33">x = \ -x_0</script>
<nobr><span class="math" id="MathJax-Span-306" style="width: 2.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-307"><span class="mi" id="MathJax-Span-308" style="font-family: STIXGeneral-Italic;">y</span><span class="mo" id="MathJax-Span-309" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-310" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.806em; vertical-align: -0.281em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-34">y = \ </script><nobr><span class="math" id="MathJax-Span-311" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.623em, -0.601em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-312"><span class="msubsup" id="MathJax-Span-313"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-314" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-315" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.853em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-35">y_0</script>
用矩阵表示就是:
如果对称轴是y = x,如图:
那么,
很容易可以解得:
<nobr><span class="math" id="MathJax-Span-316" style="width: 3.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 3.013em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.916em, -0.604em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-317"><span class="mi" id="MathJax-Span-318" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span class="mo" id="MathJax-Span-319" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-320" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span><span class="msubsup" id="MathJax-Span-321"><span style="display: inline-block; position: relative; width: 0.969em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.767em, -0.604em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-322" style="font-family: STIXGeneral-Italic;">x<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.003em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.094em; left: 0.51em;"><span class="mn" id="MathJax-Span-323" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.758em; vertical-align: -0.233em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-36">x = \ x_0</script>
<nobr><span class="math" id="MathJax-Span-324" style="width: 2.15em; display: inline-block;"><span style="display: inline-block; position: relative; width: 2.051em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mrow" id="MathJax-Span-325"><span class="mi" id="MathJax-Span-326" style="font-family: STIXGeneral-Italic;">y</span><span class="mo" id="MathJax-Span-327" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;">=</span><span class="mtext" id="MathJax-Span-328" style="font-family: STIXGeneral-Regular; padding-left: 0.313em;"></span></span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.806em; vertical-align: -0.281em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-37">y = \ </script><nobr><span class="math" id="MathJax-Span-329" style="width: 1.083em; display: inline-block;"><span style="display: inline-block; position: relative; width: 1.026em; height: 0px; font-size: 104%;"><span style="position: absolute; clip: rect(1.546em, 1000em, 2.623em, -0.601em); top: -2.179em; left: 0em;"><span class="mrow" id="MathJax-Span-330"><span class="msubsup" id="MathJax-Span-331"><span style="display: inline-block; position: relative; width: 0.972em; height: 0px;"><span style="position: absolute; clip: rect(1.931em, 1000em, 2.962em, -0.601em); top: -2.564em; left: 0em;"><span class="mi" id="MathJax-Span-332" style="font-family: STIXGeneral-Italic;">y</span><span style="display: inline-block; width: 0px; height: 2.564em;"></span></span><span style="position: absolute; top: -2.002em; left: 0.513em;"><span class="mn" id="MathJax-Span-333" style="font-size: 70.7%; font-family: STIXGeneral-Regular;">0</span><span style="display: inline-block; width: 0px; height: 2.244em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 2.179em;"></span></span></span><span style="border-left-width: 0em; border-left-style: solid; display: inline-block; overflow: hidden; width: 0px; height: 0.853em; vertical-align: -0.328em;"></span></span></nobr><script type="math/tex" id="MathJax-Element-38">y_0</script>
用矩阵表示就是:
同样的道理,如果对称轴是y = -x,那么用矩阵表示就是:
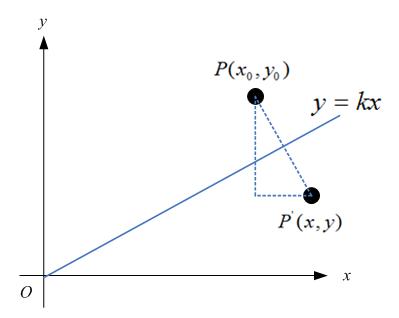
特殊地,如果对称轴是y = kx,如下图:
那么,
很容易可解得:
用矩阵表示就是:
当k = 0时,即y = 0,也就是对称轴为x轴的情况;当k趋于无穷大时,即x = 0,也就是对称轴为y轴的情况;当k =1时,即y = x,也就是对称轴为y = x的情况;当k = -1时,即y = -x,也就是对称轴为y = -x的情况。不难验证,这和我们前面说到的4中具体情况是相吻合的。
如果对称轴是y = kx + b这样的情况,只需要在上面的基础上增加两次平移变换即可,即先将坐标原点移动到(0, b),然后做上面的关于y = kx的对称变换,再然后将坐标原点移回到原来的坐标原点即可。用矩阵表示大致是这样的:
需要特别注意:在实际编程中,我们知道屏幕的y坐标的正向和数学中y坐标的正向刚好是相反的,所以在数学上y = x和屏幕上的y = -x才是真正的同一个东西,反之亦然。也就是说,如果要使图片在屏幕上看起来像按照数学意义上y = x对称,那么需使用这种转换:
要使图片在屏幕上看起来像按照数学意义上y = -x对称,那么需使用这种转换:
关于对称轴为y = kx 或y = kx + b的情况,同样需要考虑这方面的问题。
参考:
http://blog.csdn.net/pathuang68/article/details/6991867
基本方法解析
构造函数
public Matrix()
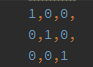
public Matrix(Matrix src)构造函数有两个,第一个是直接创建一个单位矩阵,第二个是根据提供的矩阵创建一个新的矩阵(采用deep copy)
单位矩阵如下:
isIdentity与isAffine
public boolean isIdentity()//判断是否是单位矩阵
public boolean isAffine()//判断是否是仿射矩阵是否是单位矩阵很简单,就不做讲解了,这里是否是仿射矩阵可能大家不好理解。
首先来看看什么是仿射变换。仿射变换其实就是二维坐标到二维坐标的线性变换,保持二维图形的“平直性”(即变换后直线还是直线不会打弯,圆弧还是圆弧)和“平行性”(指保持二维图形间的相对位置关系不变,平行线还是平行线,而直线上点的位置顺序不变),可以通过一系列的原子变换的复合来实现,原子变换就包括:平移、缩放、翻转、旋转和错切。这里除了透视可以改变z轴以外,其他的变换基本都是上述的原子变换,所以,只要最后一行是0,0,1则是仿射矩阵。
####rectStaysRect
public boolean rectStaysRect()判断该矩阵是否可以将一个矩形依然变换为一个矩形。当矩阵是单位矩阵,或者只进行平移,缩放,以及旋转90度的倍数的时候,返回true。
####reset
public void reset()重置矩阵为单位矩阵。
####setTranslate
public void setTranslate(float dx, float dy)设置平移效果,参数分别是x,y上的平移量。
效果图如下:
代码:
Matrix matrix = new Matrix();
canvas.drawBitmap(bitmap, matrix, paint);
matrix.setTranslate(100, 1000);
canvas.drawBitmap(bitmap, matrix, paint);setScale
public void setScale(float sx, float sy, float px, float py)
public void setScale(float sx, float sy)两个方法都是设置缩放到matrix中,sx,sy代表了缩放的倍数,px,py代表缩放的中心。这里跟上面比较类似不做讲解了。
setRotate
public void setRotate(float degrees, float px, float py)
public void setRotate(float degrees)和上面类似,不再讲解。
setSinCos
public void setSinCos(float sinValue, float cosValue, float px, float py)
public void setSinCos(float sinValue, float cosValue)这个方法乍一看可能有点蒙,其实在前面的原理中,我们讲解了一个旋转的例子,他最终的矩阵效果是这样的:
其实旋转,就是使用了这样的matrix,显而易见,这里的参数就清晰了。
sinValue:对应图中的sin值
cosValue:对应cos值
px:中心的x坐标
py:中心的y坐标
看一个示例,我们把图像旋转90度,那么90度对应的sin和cos分别是1和0。
看代码如下:
Matrixmatrix = new Matrix();
matrix.setSinCos(1, 0, bitmap.getWidth() / 2, bitmap.getHeight() / 2);
canvas.drawBitmap(bitmap, matrix, paint);setSkew
public void setSkew(float kx, float ky, float px, float py)
public void setSkew(float kx, float ky)错切,这里kx,ky分别代表了x,y上的错切因子,px,py代表了错切的中心。不了解错切了在前面canvas变换中去查看,这里不再讲解。
setConcat
public boolean setConcat(Matrix a,Matrix b)将当前matrix的值变为a和b的乘积,它的意义在下面的 进阶方法中来探讨。
进阶
上面的基本方法中,有关于变换的set方法都可以带来不同的效果,但是每个set都会把上个效果清除掉,例如依次调用了setSkew,setTranslate,那么最终只有setTranslate会起作用,那么如何才和将两种效果复合呢。Matrix给我们提供了很多方法。但是主要都是2类:
preXXXX:以pre开头,例如preTranslate
postXXXX:以post开头,例如postScale
他们分别代表了前乘,和后乘。看一段代码:
Matrix matrix = new Matrix();
matrix.setTranslate(100, 1000);
matrix.preScale(0.5f, 0.5f);这里matrix前乘了一个scale矩阵,换算成数学式如下:
从上面可以看出,最终得出的matrix既包含了缩放信息也有平移信息。
后乘自然就是matrix在后面,而缩放矩阵在前面,由于矩阵前后乘并不等价,也就导致了他们的效果不同。我们来看看后乘的结果:
可以看到,结果跟上面不同,并且这也不是我们想要的结果,这里缩放没有更改,但是平移被减半了,换句话说,平移的距离也被缩放了。所以需要注意前后乘法的关系。
来看看他们对应的效果图:
前乘:
后乘:
可以明显看到,后乘的平移距离受了影响。
了解清除了前后乘的意义,在使用的过程中,多个效果的叠加时,一样要注意,否则效果达不到预期。
其他方法
matrix除了上面的方法外,还有一些其他的方法。
setRectToRect
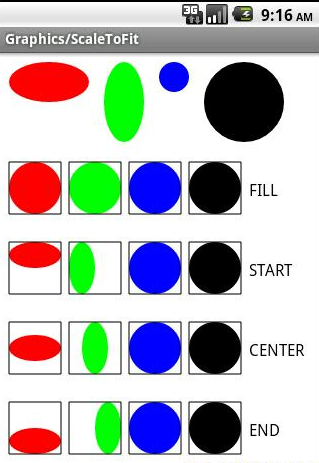
public boolean setRectToRect(RectF src, RectF dst, ScaleToFit stf)将rect变换成rect,上面的rectStaysRect已经说过,要保持rect只能做缩放平移和选择90度的倍数,那么这里其实也是一样,只是这几种变化,这里通过stf参数来控制。
ScaleToFit 有如下四个值:
- FILL: 可能会变换矩形的长宽比,保证变换和目标矩阵长宽一致。
- START:保持坐标变换前矩形的长宽比,并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。左上对齐。
- CENTER: 保持坐标变换前矩形的长宽比,并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。
- END:保持坐标变换前矩形的长宽比,并最大限度的填充变换后的矩形。至少有一边和目标矩形重叠。右下对齐。
这里使用谷歌的api demo的图片作为例子:
setPolyToPoly
public boolean setPolyToPoly(float[] src, int srcIndex,float[] dst, int dstIndex,int pointCount)
通过指定的0-4个点,原始坐标以及变化后的坐标,来得到一个变换矩阵。如果指定0个点则没有效果。
下面通过例子分别说明1到4个点的可以达到的效果:
1个点,平移
只指定一个点,可以达到平移效果:
代码如下:
float[] src = {0, 0};
int DX = 300;
float[] dst = {0 + DX, 0 + DX};
matrix.setPolyToPoly(src, 0, dst, 0, 1);
canvas.drawBitmap(bitmap, matrix, paint);2个点,旋转或者缩放
两个点,可以达到旋转效果或者缩放效果,缩放比较简单,这里我们来看旋转效果,一个点指定中心,一点指出旋转的效果。
代码:
int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {bw / 2, bh / 2, bw, 0};
float[] dst = {bw / 2, bh / 2, bw / 2 + bh / 2, bh / 2 + bw / 2};
matrix.setPolyToPoly(src, 0, dst, 0, 2);
canvas.drawBitmap(bitmap, matrix, paint);图片的中心点作为旋转的中心,前后不变,右上角变化到了下方,所以导致图片旋转了90度。
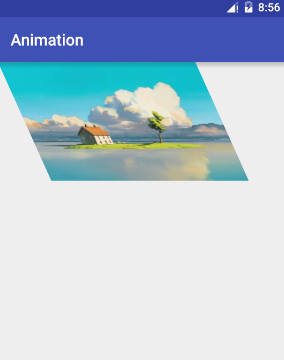
3个点,错切
使用3个点,可以产生错切效果,指定3个顶点,一个固定,另外两个移动。
看图:
代码如下:
Matrix matrix = new Matrix();
int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {0,0, 0, bh,bw,bh};
float[] dst = {0, 0, 200, bh, bw + 200, bh};
matrix.setPolyToPoly(src, 0, dst, 0, 3);
canvas.drawBitmap(bitmap, matrix, paint);4个点,透视
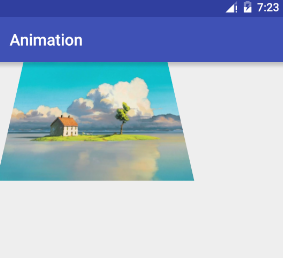
透视就是观察的角度变化了。导致投射到平面上的二维图像变化了。
我们看下面的例子,更容易理解:
图片看起来好像倾斜了,实现特别简单:
Matrix matrix = new Matrix();
int bw = bitmap.getWidth();
int bh = bitmap.getHeight();
float[] src = {0, 0, 0, bh, bw, bh, bw, 0};
int DX = 100;
float[] dst = {0 + DX, 0, 0, bh, bw, bh, bw - DX, 0};
matrix.setPolyToPoly(src, 0, dst, 0, 4);
canvas.drawBitmap(bitmap, matrix, paint);可以看到,只是把左右两个顶点往里面收拢了,这样就得出了一个有3d效果的透视图。
invert
public boolean invert(Matrix inverse)反转当前矩阵,如果能反转就返回true并将反转后的值写入inverse,否则返回false。当前矩阵*inverse=单位矩阵。
反转前后有什么效果,我们来看看示例:
可以看到,反转之后,其实是对效果的一种反转。
mapPoints
public void mapPoints(float[] dst, int dstIndex, float[] src, int srcIndex,int pointCount)
public void mapPoints(float[] dst, float[] src)
public void mapPoints(float[] pts)映射点的值到指定的数组中,这个方法可以在矩阵变换以后,给出指定点的值。
dst:指定写入的数组
dstIndex:写入的起始索引,x,y两个坐标算作一对,索引的单位是对,也就是经过两个值才加1
src:指定要计算的点
srcIndex:要计算的点的索引
pointCount:需要计算的点的个数,每个点有两个值,x和y。
mapVectors
public void mapVectors(float[] dst, int dstIndex, float[] src, int srcIndex,int vectorCount)
public void mapVectors(float[] dst, float[] src)
public void mapVectors(float[] vecs)与上面的mapPoionts基本类似,这里是将一个矩阵作用于一个向量,由于向量的平移前后是相等的,所以这个方法不会对translate相关的方法产生反应,如果只是调用了translate相关的方法,那么得到的值和原本的一致。
mapRect
public boolean mapRect(RectF dst, RectF src)
public boolean mapRect(RectF rect)返回值即是调用的rectStaysRect(),这个方法前面有讲过,这里把src中指定的矩形的左上角和右下角的两个点的坐标,写入dst中。
mapRadius
public float mapRadius(float radius)返回一个圆圈半径的平均值,将matrix作用于一个指定radius半径的圆,随后返回的平均半径。
以上基本解析完毕了所有matrix的方法,以及一些高阶用法,本篇文章就到这里






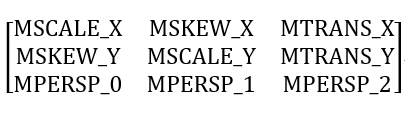
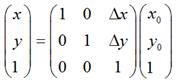
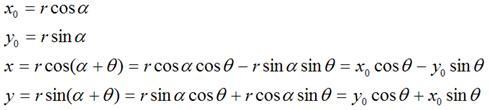
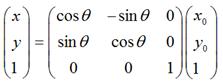
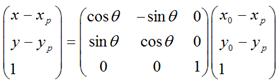
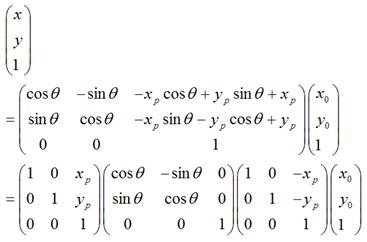
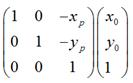
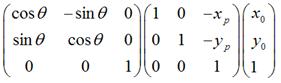
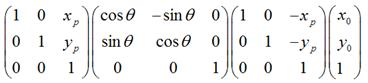
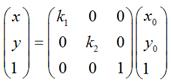
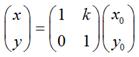
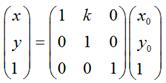
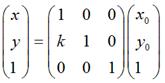
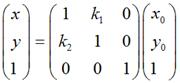
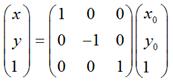
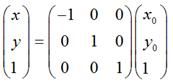
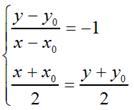
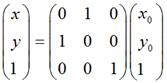
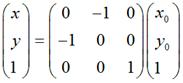
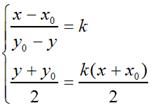
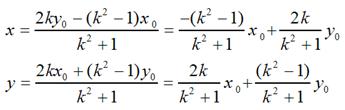
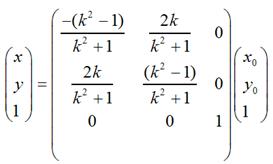
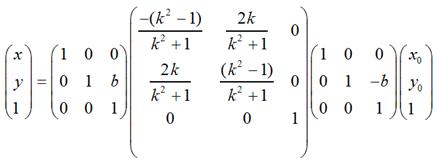
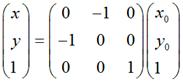
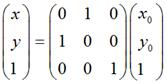

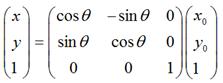




















 2379
2379

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








