把循环小数化为分数

把循环小数化为分数

在计算机中，使用float或者double来存储小数是不能得到精确值的。如果你希望得到精确计算结果，最好是用分数形式来表示小数。有限小数或者无限循环小数都可以转化为分数。比如：

0.9 = 9/10

0.333（3）= 1/3（括号中的数字表示是循环节）

当然一个小数可以用好几种分数形式来表示。如：

0.333（3）= 1/3 = 3/9

给定一个有限小数或者无限循环小数，你能否以分母最小的分数形式来返回这个小数呢？如果输入为循环小数，循环节用括号标记出来。下面是一些可能的输入数据，如0.3、0.30、0.3（000）、0.3333（3333）、……

有限小数化为分数比较简单，下面重点分析如何把循环小数化为分数？

分析：看到这么一个题目，该如何下手呢？这也是困惑我的问题，怎么来解决这个循环的问题？所以问题的核心是如何搞定循环部分，找出是什么原因到这了这个循环的产生。

既然我们很容易解决有限小数，那么我们就从有限小数的转化入手，看看两者之间有什么联系，能否找到突破口，以分析0.3和0.3333（3333）为例。

第一种思路：找出什么原因导致循环（从一个我们能解决掉的简单例子入手）

0.3转化为分数是3/10，并且有3/10 < 0.3333（3333）,那么接下来就是如何把3/10变大一点。有两种方法可以让它增大，一是分子增加x,分母不变，但这样最终结果还是有限小数；二是让分母减小x，分子不变，这就有可能变为循环小数，也就是：3/10→ 3/(10-x)。那么x应该是多少呢？看来这个问题找到了一点突破口了。先分析最简单的，取x=1。下面来做一下两者的计算过程：

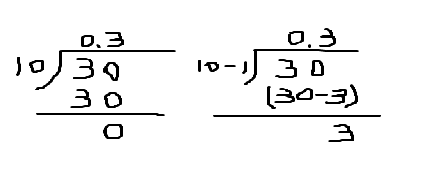
由上面的计算过程可知，分母减少x，余数为3*x。在这里，我们只需要x为1，则余数与分子相等，这不又还原到了刚开始，所以导致不断的除下去。下面来分析另一个例子，0.003（3）：

在这里x=100。

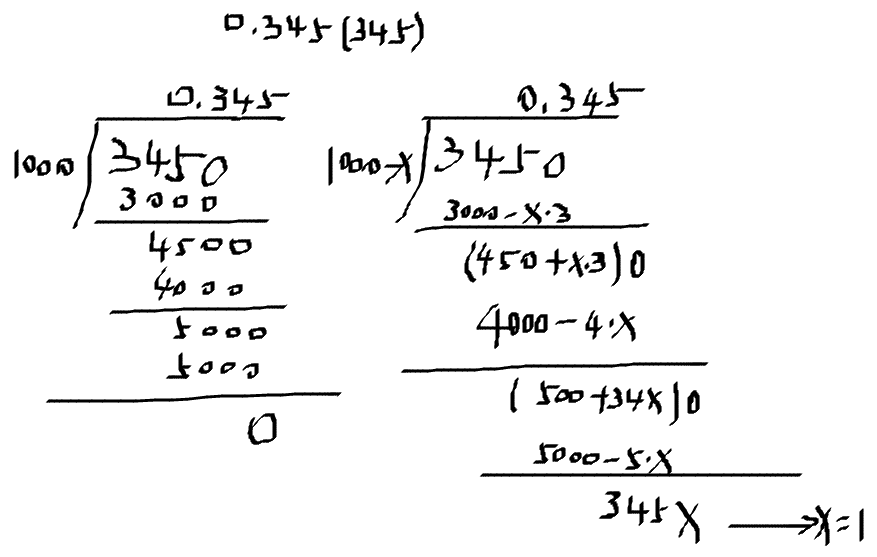
所以我们已经找到了产生循环的原因：使每次的余数是分子的10ⁿ（n>=0）倍。

如果遇见这种情况呢0.4354(4)呢？那好办，0.4354(4)=0.435+0.0004(4)

总结：在很多情况下，一个已经容易解决或者很相似的问题，往往能给我们当前的问题带来一些思路。所以当没有思路是，不妨从一个已经解决的问题入手。

思路二：去除循环部分（把无限变有限）

令Y=0. b₁b₂…b_m，那么

10^m*Y=b₁b₂…b_m.（b₁b₂…b_m）

10^m*Y=b₁b₂…b_m+0.（b₁b₂…b_m）

10^m*Y-Y=b₁b₂…b_m

Y= b₁b₂…b_m/（10^m-1）

具体分析见：http://www.msra.cn/Articles/ArticleItem.aspx?Guid=9bd3f0ad-c5c0-4ad7-9750-d109377374b6#