数据库--ER模型、函数依赖、无损分解、关系代数

ER模型的基本概念，以及如何绘制E-R图；

实体：客观存在的可以相互区别的事物，也可以是抽象的事件。如：一场足球赛等。

实体在ER图中用矩形表示

属性：实体有很多特性，每一个特性成为属性。每个属性的值域可以是整数型，实数型等。

属性用椭圆形来表示。

联系（Relationship）：

1联系：如果实体集E1中的每个实体最多只能和实体集E2中一个实体有联系，反之亦然，那么实体集E1对E2的联系成为一对一联系，记为1:1

N联系：一对多，记为1：N。

M:N联系：多对多联系，记为M:N

画ER图：

找出实体，联系，最后把属性补充上去。

函数依赖：

定义：设R（U）是属性集U上的关系模式。X，Y是U的子集。若对于R(U)的任意一个可能的关系r，r中不可能存在两个元组在X上的属性值相等，而在Y上的属性值不等，则称X函数确定Y或Y函数依赖于X，计作X→Y。

首先明白关系模式和属性集的概念。属性集可以理解为N条记录，每条记录中有主键和属性。

X，Y是U的子集，即X，Y为其中的两列数据。

对于R(U)的任意一个可能的关系r：r可以理解为主键和某一字段属性的关系，或者某两个不相关属性之间的关系。这个关系不是确定的。

最后一句话的意思就是说在X属性列中不可能存在两个元组在X中相等，而在Y属性列中相等。

例：主键X可以确定后面的一列属性Y，则可以说X函数确定Y或Y函数依赖于X

两列非主属性X，Y，X不能确定Y，称为X函数不能确定Y，则没有依赖惯性系。

完全函数依赖：

定义：在R(U)中，如果X→Y，并且对于X的任何一个真子集X’不依赖于Y，则称Y对X完全函数依赖。记作X→^FY

即X是一个集合，而整个集合才能确定Y而其中的一个真子集X’不能确定Y才是完全函数依赖。

部分函数依赖：

若X→Y，但Y不完全函数依赖于X，则称Y对X部分函数依赖》记作X→^PY

传递函数依赖：

在R(U) 中，如果X→Y，（Y不包含于X），Y不函数依赖于X，Y函数依赖于Z，则称Z对X传递函数依赖。

无损分解：

在此简单的可以理解为可以还原的为无损分解，如果不可以还原，则为有损分解。

那么，判断是否为无损分解，则判断是否能还原即可。下面以一例题讲解。

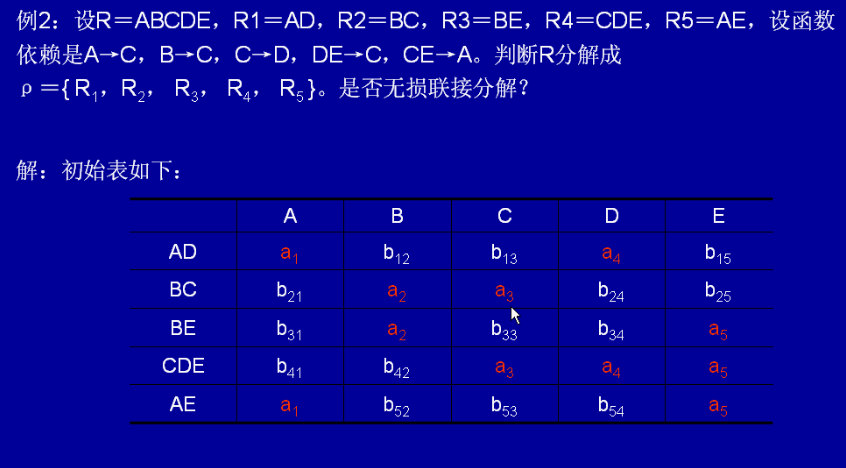
首先，行为R中的元素，列为R1-R5。

第一步：R1，R2……中有没有所对应的ABCDE，如果有则用a1，a2表示

第二步：看A→C，看AC两列，a1→b13，所以AE列a1→b13把原来的b53改为b13（以小的为标准改）

第三步：看B→C，类似第二步。

……

下面的依次类推：DE→C是一样的。

另外一种方法：

如果R的分解为p=｛R1，R2｝，F为R所满足的函数依赖集合，分解p具有无损链接性的充分必要条件是：

R1∩R2→（R1-R2）或R1∩R2→（R2-R1） PS：-操作为R1中去除R1和R2的公共属性所组成。

关系代数：

五种基本运算：并，差，笛卡尔积，选择和投影。此外还有除。

关系代数概念：是一种抽象的查询语言，是一种代数的符号，其中的查询时通过向关系附加特定的操作符来表示的。它包括一个对表进行操作的集合。（关系代数其实就是对关系的一个运算，而这种对关系的运算就是一种查询语言）

1.并（Union，∪）：R∪S的联合就是所有在R里面有，或S里面有，火灾两个表里面都有的记录集合。

2.差（Difference，-）：计算两个表的区别的集合。R-S是在R里面却不在S里面的记录的集合。

3.笛卡尔积（Product，X）：计算两个关系的笛卡尔乘积。令RK1元的表，令S为有k2元的表。RxS是所有k1+k2元记录的集合，其前k1个元素来自R里德一条记录，而后k2个元素来自S里的一条记录。

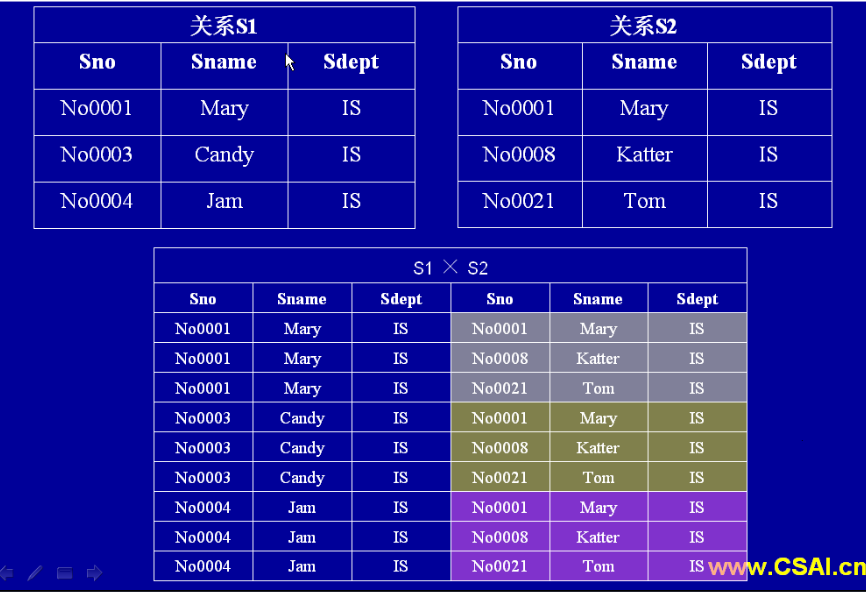
4.投影（Project，用符号π表示）：从一个表中选取几列的操作，

5.选择（Select，用符号σ表示）：从一个表里选取n行记录

6.交（Intersection，用符号∩表示）：计算两个表集合理论上的交集。给出表R和S，R∩S是同时在R和S里面的记录的集合。

7.连接（Join）：两个表先进行笛卡尔乘积，根据相同的属性进行选择，然后用投影把重复的列去掉。即为连接。

8.除（Division，用÷来表示）：有两个关系R(X,Y)与关系S(Z)，其中，X,Y,Z为属性集合。假设Y和Z具有相同的属性个数，且对应属性出自相同域。关系R(X,Y)÷S(Z)所得的商关系是关系R在属性X上投影的一个子集，该子集和S(Z)的笛卡尔积必须包含R(X,Y)中。记为R÷S。

R在属性X上投影的一个子集：即X属性中的一个子集，即可能为几行数据，后面一句的意思即这个子集中原来对应的数据必须和Z属性中的一样。即为除关系。