Big Number
Time Limit: 2000/1000 MS (Java/Others)
Memory Limit: 65536/32768 K (Java/Others)
Problem Description
In many applications very large integers numbers are required. Some of these applications are using keys for secure transmission of data, encryption, etc. In this problem you are given a number, you have to determine the number of digits in the factorial of the number.
Input
Input consists of several lines of integer numbers. The first line contains an integer n, which is the number of cases to be tested, followed by n lines, one integer 1 ≤ n ≤ 10
7on each line.
Output
The output contains the number of digits in the factorial of the integers appearing in the input.
Sample Input
2 10 20
这道题目应用斯特灵公式来求解:
斯特灵公式是一条用来取n阶乘近似值的数学公式。一般来说,当n很大的时候,n阶乘的计算量十分大,所以斯特灵公式十分好用,而且,即使在n很小的时候,斯特灵公式的取值已经十分准确。
公式为:
这就是说,对于足够大的整数n,这两个数互为近似值。更加精确地:
或
//此题必须用公式才能AC,数据规模太大了
//Stirling公式: n! = ((2*pi*n)^(1/2))*((n/e)^n); 前提是n > 3
//由此可以导出lg(n!)=(lg(2*pi)+lg(n))/2 + n*(lg(n)-lg(e));
#include<iostream>
#include<cmath>
using namespace std;
const long double c1=0.798179868358; //lg(2*pi)
const long double c2=0.434294481903; //lg(e)
int main()
{
int n,t;
cin>>t;
int s;
long double c3;//特别要注意精度的问题,此处c3应为long double型,否则很容易丢失精度,造成答案错误
for(int i=0;i<t;i++)
{
cin>>n;
c3=log10((double)n);
if(t>3)
s=(c3+c1)/2+n*(c3-c2)+1;//由于10^0=1,10^1=10……,故在最后还要加一个1
//s=?发生自动类型转换,如10^2.5=x,则s=2+1,则说明x!介于10^2与10^3之间,位数为3!
else
s=1;
cout<<s<<endl;
}
return 0;
}





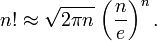
















 1333
1333

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








