小波变换网文精粹:小波变换教程(十)
原文:ROBI POLIKAR. THE ENGINEER'S ULTIMATE GUIDE TO WAVELET ANALYSIS:The Wavelet Tutorial
网址:http://users.rowan.edu/~polikar/WAVELETS/WTtutorial.html
译文转自:http://blog.163.com/renfengyuee@126/blog/static/3594313620109118101583/
十、小波变换基础:短时傅立叶变换(三)
为了更明白的理解这个问题,让我们看一些例子:我现在有四个不同宽度的窗函数,我们将一一用这些窗函数做傅立叶变换,看看到底发生了什么:
我们用到的窗函数是一个简单的高斯函数,如下式:
w(t)=exp(-a*(t^2)/2);
其中,a代表窗口宽度,t代表时间。接下来这幅图显示了四个用宽度a来决定的不同支撑域的窗函数。请忽略a的值,因为用来计算的时间间隔同时决定了函数。注意四幅图的宽度。上面这个例子中的时间以秒为单位,a=0.001,接下来显示用不同的窗口进行快速傅立叶变换后的图形。

图2.10
首先看第一个最窄的窗口。我们期望的结果是变换结果应具有好的时间分别率和差的频率分辨率。

图2.11
上面的图显示了快速傅立叶变换结果。为了以一个更好的角度看图,我们的图以鸟瞰图显示。注意到四个尖峰在时间上被准确的区分开了,还要注意,在频率轴,每个尖峰都横跨了一个频率带,而不是对应一个确切的频率值。现在让我们看看更宽一点的窗函数,看第三幅图(第二幅图在第一个例子中已经展示过了)。

图2.12
注意到,不像第一幅图,在时间轴上,四个尖峰没有很好的的区分开来。但是在频域内分辨率却明显提高了。现在让我们看看最宽的窗口宽度,看看到底发生了什么:
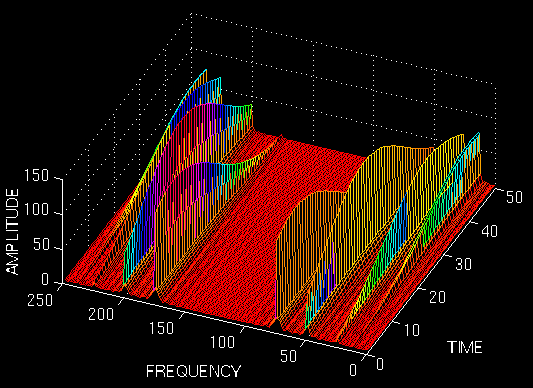
图 2.13
现在任何人都不应该再赶到惊奇了,因为本来我们就知道时间分辨率会超级差(我的意思是差到不能再差)。
这些例子应该展示了快速傅立叶变换存在的分辨率问题。每个将要用到快速傅立叶变换的人都会面临这个问题。用什么样的窗函数?用窄窗可以得到较高的时间分辨率,但是较低的频率分辨率,用宽窗仍然也会面临稳定性的问题。问题集中到如何选择窗函数上来了。这个窗要能够在整个分析过程中一直可用。答案当然是只与应用相关:如果原始信号中的频率分量已经被区分出来了,那么我们就可以牺牲一部分频率分辨率来追求更高的时间分辨率。但是如果情况不是这样的话,那么选择一个好的窗函数比选择一个值得投资的股票更难。
现在,你应该理解为什么要提出小波变换了吧?我们后文中将会看到,小波变换在一定程度上解决了这个分辨率的问题。
第二大部分结束了。教程的第三部分主要讲连续小波变换。如果到目前为止你还没有碰到什么麻烦,上面讲的东西你都能理解,那么你可以开始这个理解小波变换基本理论的终极挑战了。
PS:原文pdf打包下载地址:http://download.csdn.net/detail/deepdsp/4061006























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








