【排序】七大排序特性分析及总结

0.前言

1. 排序的概念：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
2. 稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
3. 内部排序：数据元素全部放在内存中的排序。
4. 外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

常见的排序算法：

1.直接插入排序

1. 时间复杂度
   最坏：逆序：1+2+3+4+…+N 等差数列：O(N^2).
   最好：顺序有序：O(N) 只比较不插入数据
   综上，插入排序的时间复杂度为O(N^2)。
2. 空间复杂度
   插入排序的空间复杂度：O(1)
3. 稳定性
   插入排序算法是一种稳定的算法

2.冒泡排序

1. 时间复杂度
   最坏：逆序：1+2+3+4+…+N 等差数列：O(N^2)
   最好：顺序有序：O(1)
   综上，冒泡排序的时间复杂度为O(N)。
2. 空间复杂度
   冒泡排序的空间复杂度为O(1)。
3. 稳定性
   冒泡排序算法是一种稳定的算法

3.希尔排序

1. 时间复杂度

希尔排序的时间复杂度不好计算，因为gap的取值方法很多，导致很难去计算，因此在好些书中给出的希尔排序的时间复杂度都不固定：

因为咋们的gap是按照Knuth提出的方式取值的，而且Knuth进行了大量的试验统计，我们就按照：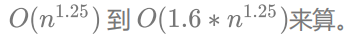

2. 空间复杂度
希尔排序的空间复杂度为O(1)
3. 稳定性
希尔排序算法是一种不稳定的算法

4.直接选择排序

1. 直接选择排序思考非常好理解，但是效率不是很好。实际中很少使用
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：不稳定

5. 堆排序

1. 时间复杂度
   堆排序包括两个阶段，初始化建堆和重建堆。所以堆排序的时间复杂度由这两方面组成，下面分别进行分析。
   初始化建堆：
   
   重新建堆：
   和建堆的思路差不多，交换节点为O(1)交换n次，所以遍历消耗时间O(n),最坏情况下，对n-1个节点建堆的过程中，耗时为O(logn)，所以时间复杂度为n*log(n)
   综上，总的时间复杂度为O(n) + O(nlogn),考虑n>=2时，logn比1大，所以最终取时间复杂度为O(nlogn)
2. 空间复杂度
   堆排序的空间复杂度为O(1).
3. 稳定性
   堆排序是一种不稳定的算法。

6.快速排序

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)
   

3. 空间复杂度：O(logN)

4. 稳定性：不稳定

7.归并排序

1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度：O(N*logN)
3. 空间复杂度：O(N)
4. 稳定性：稳定

8.测试各个排序算法

void TestOP()
{
	srand(time(0));
	const int N = 100000;
	int* a1 = (int*)malloc(sizeof(int) * N);
	int* a2 = (int*)malloc(sizeof(int) * N);
	int* a3 = (int*)malloc(sizeof(int) * N);
	int* a4 = (int*)malloc(sizeof(int) * N);
	int* a5 = (int*)malloc(sizeof(int) * N);
	int* a6 = (int*)malloc(sizeof(int) * N);
	int* a7 = (int*)malloc(sizeof(int) * N);

	for (int i = 0; i < N; ++i)
	{
		a1[i] = rand();
		a2[i] = a1[i];
		a3[i] = a1[i];
		a4[i] = a1[i];
		a5[i] = a1[i];
		a6[i] = a1[i];
		a7[i] = a1[i];
	}

	int begin1 = clock();
	InsertSort(a1, N);
	int end1 = clock();

	int begin2 = clock();
	ShellSort(a2, N);
	int end2 = clock();

	int begin3 = clock();
	BubbleSort(a3, N);
	int end3 = clock();

	int begin4 = clock();
	SelectSort(a4, N);
	int end4 = clock();

	int begin5 = clock();
	HeapSort(a5, N);
	int end5 = clock();

	int begin6 = clock();
	QuickSort1(a6, 0, N - 1);
	int end6 = clock();

	int begin7 = clock();
	MergeSort(a7, N);
	int end7 = clock();

	printf("InsertSort:%d\n", end1 - begin1);
	printf("ShellSort:%d\n", end2 - begin2);
	printf("BublleSort:%d\n", end3 - begin3);

	printf("SelectSort:%d\n", end4 - begin4);
	printf("HeapSort:%d\n", end5 - begin5);
	printf("QuickSort1:%d\n", end6 - begin6);
	printf("MergeSort:%d\n", end7 - begin7);

	free(a1);
	free(a2);
	free(a3);
	free(a4);
	free(a5);
	free(a6);
	free(a7);
}

int main()
{
	TestOP();
	return 0;
}