概念定义
连通分量的定义
独立且完整的连通块。
如下图就是三个连通分量。
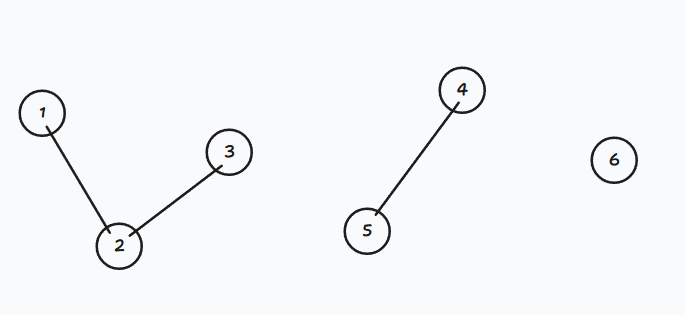
有向图的强连通分量 SCC
由原图的某一部分(顶点和连接这些顶点的有向边)组成。 在这个子图中, 保持 “极大” 与 强连通性。
强连通性
一个有向图(或子图)是强连通的,指的是对于其中任意两个顶点
u
u
u 和
v
v
v,都同时存在以下两条路径:
* 一条从
u
u
u 到
v
v
v 的有向路径。
* 一条从
v
v
v 到
u
u
u 的有向路径。
极大
一个强连通子图被称为“极大”,意味着你不能再从原图 G G G 中添加任何其他的顶点,还能使这个子图保持强连通。
总结:一个强连通分量是一个包含了所有能相互到达的顶点的“闭环集合”,并且这个集合已经不能再扩大了。
示例
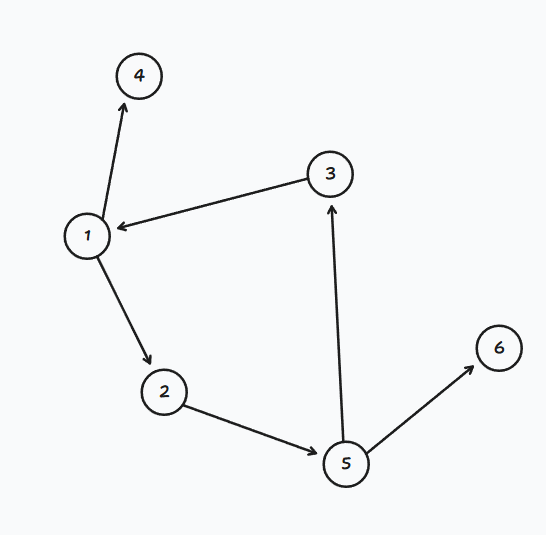
这个有向图包含 3 个强连通分量:
- SCC 1:
{1, 2, 3, 5} - SCC 2:
{4} - SCC 3:
{6}
求强连通分量的目的
在某些题目中存在环,且在同一个环中的点有某种相同的性质,那么通过求出强连通分量,再进行缩点,将原图转换成拓扑图(有向无环图 DAG)会大大简化程序的复杂度,就可以在DAG上递推,得到正确的答案。
算法 : Tarjan 求 SCC
Tarjan 算法是一种基于深度优先搜索(DFS)的线性时间复杂度算法。它通过一次 DFS 遍历,就能找出有向图中的所有强连通分量。
核心数据结构
算法为图中的每个顶点 u 维护两个关键的整数值:
-
dfn[u](时间戳)- 定义:在 DFS 过程中,顶点
u被首次访问到的“时间戳”或“次序编号”。dfn值是严格递增且唯一的。通常用一个全局计数器来实现。
- 定义:在 DFS 过程中,顶点
-
low[u]- 定义:从顶点
u出发,通过 DFS 搜索树中的边以及最多一条非树边(non-tree edge),能够到达的所有顶点中最小的dfn值。 - 通俗解释:
low[u]代表了u或u的 DFS 子树中的节点,能够通过返祖边(back edge)回溯到的最早的祖先节点的dfn值。
- 定义:从顶点
除了这两个数组,算法还需要一个栈来存储当前 DFS 路径上的顶点。一个顶点进入 DFS 递归时入栈,在它所属的 SCC 被完全找到后出栈。
算法流程
算法的主体是一个 DFS 函数,通常命名为 tarjan(u)。
-
初始化:
dfn和low数组初始化为某个标记值(如 0 或 -1),表示未访问。- 时间戳计数器
timestamp初始化为 0。 - 栈
S为空。 - 遍历所有顶点,如果顶点
i未被访问,则调用tarjan(i)。
-
tarjan(u)函数执行过程:
a. 标记访问和入栈:- 将
u标记为已访问。 - 设置
dfn[u] = low[u] = ++timestamp。这表示u最初只能到达它自己。 - 将
u压入栈S中。
b. 遍历
u的邻接点v:
对于从u出发的每一条边(u, v):-
Case 1:
v未被访问- 递归调用
tarjan(v)。 - 递归返回后,
v及其子树的low值已经计算完毕。u可以通过树边(u, v)到达v的子树所能到达的一切节点。因此,用low[v]来更新low[u]:
low[u] = min(low[u], low[v])
- 递归调用
-
Case 2:
v已被访问,且v在栈S中- 这说明边
(u, v)是一条返祖边(Back Edge),它从u指向了 DFS 树中u的一个祖先v。 - 这条边提供了一条从
u回到更早节点v的路径。因此,用dfn[v]来更新low[u]:
low[u] = min(low[u], dfn[v]) - 注意:这里必须用
dfn[v]而不是low[v]。因为边(u, v)直接连接到v,我们只关心这条边本身提供的回溯能力。low[v]可能是一个更小的值,但那是通过v的其他路径实现的,与(u, v)这条边无关。
- 这说明边
-
Case 3:
v已被访问,但v不在栈S中- 这说明
v属于一个已经被确定并从栈中弹出的 SCC。边(u, v)是一条横叉边(Cross Edge)或前向边(Forward Edge),它连接到另一个已经处理完毕的 SCC。这条边对于寻找u所在的 SCC 没有帮助,因此忽略它。
- 这说明
c. 判断
u是否为 SCC 的根:
当u的所有邻接点都处理完毕后,检查以下条件:
if (dfn[u] == low[u])- 条件成立的意义:
这个等式意味着u是其所在 SCC 的根节点。u及其在 DFS 树中的后代节点,都无法通过返祖边到达比u更早被访问的节点。u是这个子结构中dfn最小的节点。 - 找到一个 SCC:
此时,从栈S的顶部开始,不断弹出顶点,直到u被弹出。所有这些被弹出的顶点{..., v, u}共同构成了一个完整的强连通分量。将它们收集起来即可。
- 将
算法的关键点总结
- DFS 树:算法隐式地构建了一棵深度优先搜索树。边被分为树边、返祖边、前向边和横叉边。
low值的更新逻辑:low[u]的值是通过两条路径更新的:- 通过其子节点
v的low[v](即利用子树的回溯能力)。 - 通过直接连接到栈中祖先
v的dfn[v](即利用返祖边的回溯能力)。
- 通过其子节点
- 根节点的判定:
dfn[u] == low[u]是判定一个节点u是否为一个 SCC 根的充要条件。这个条件确保了所有能与u强连通的节点都包含在以u为根的 DFS 子树中(并且通过返祖边连接),且无法连接到u的祖先。 - 栈的作用:栈
S精确地维护了当前尚未确定所属 SCC 的所有顶点。当一个 SCC 的根被找到时,这个 SCC 的所有成员都保证在栈的顶部连续存放,使得弹出操作可以正确地收集所有成员。
算法时间复杂度
Tarjan 算法通过这种 dfn 和 low 值的设计,在一次遍历中同时完成了 DFS 探索和 SCC 的识别,其时间复杂度和空间复杂度均为 O(V + E),其中 V 是顶点数,E 是边数。
缩点经过
定义 id[x] 表示 x 点所在的 强连通分量的编号。
- 枚举每一个点 u u u
- 枚举 u u u 的所有连边, 边的另一个端点为 v v v,
- 判断 id[u] 是否等于 id[v] , 即判断, u u u 所属于的SCC和 v v v所属于的SCC 是否为同一个
- 如果不是则在新图上添加一条重节点 id[u] 到节点 id[v] 的边。
模板程序
#include <bits/stdc++.h>
using namespace std;
const int N = 2e5 + 5; // 最多有2e5个点
int n, m; // n个点,m条有向边
int dfn[N], low[N], tsp;
int stk[N], top; // 数组模拟栈
int id[N], cnt; // 记录每个点所属于的连通块, cnt 代表 SCC 的数量
bool vis[N]; // vis[u]记录 u是否在栈中
vector<int> ed[N], hs[N]; // 使用邻接表的方法存老图和新图
void tarjan(int u)
{
dfn[u] = low[u] = ++ tsp;
stk[ ++ top ] = u, vis[u] = true; // 将u压栈
for(auto v : ed[u]){
if(!dfn[v]){
tarjan(v);
low[u] = min(low[u], low[v]);
}else if(vis[v]) low[u] = min(low[u], dfn[v]);
}
if(dfn[u] == low[u]){
++ cnt;
int tp;
do{
tp = stk[ top -- ];
vis[tp] = false;
id[tp] = cnt;
}while(u != tp); // 将以u为最高点的SCC全部弹出
}
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i ++ ){
int u, v; cin >> u >> v;
ed[u].push_back(v);
}
for(int i = 1; i <= n; i ++ ) // 防止原图不是连通图
if(!dfn[i]) tarjan(i);
// 缩点
for(int i = 1; i <= n; i ++ ){
for(auto v : ed[i]){
int a = id[i], b = id[v];
if(a != b) hs[a].push_back(b);
}
}
return 0;
}
无向图的双连通分量
1. 割点
定义:
在一个无向连通图中,如果移除某个顶点 v 以及所有与它相关联的边后,剩下的图不再连通(即分裂成两个或更多个连通分量),那么顶点 v 就被称为割点。
关键性质:
一个割点至少属于两个包含该割点的点双连通分量。
示例 :
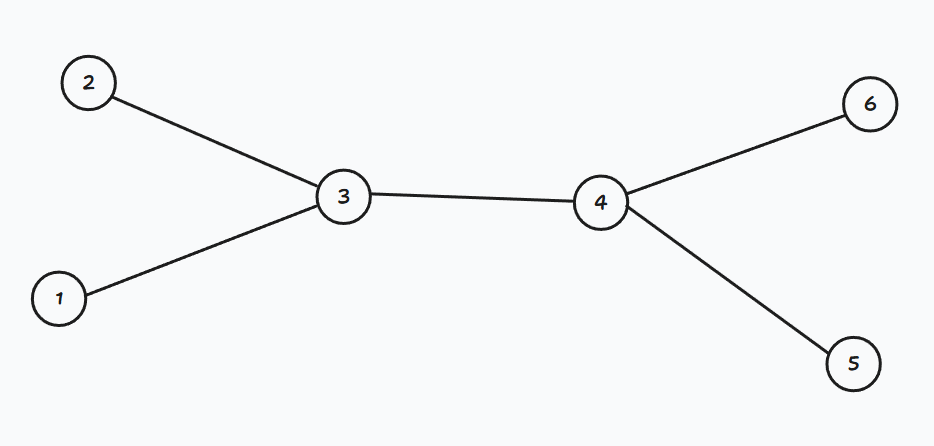
如果将3号点删去,那么图将不再连通:
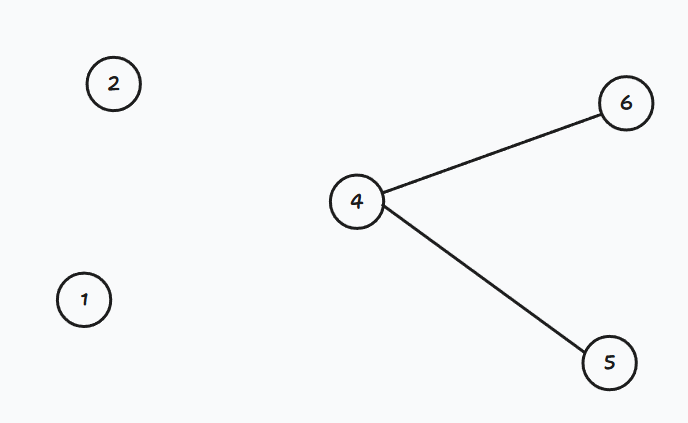
如果将4号点删去,图也不再连通:
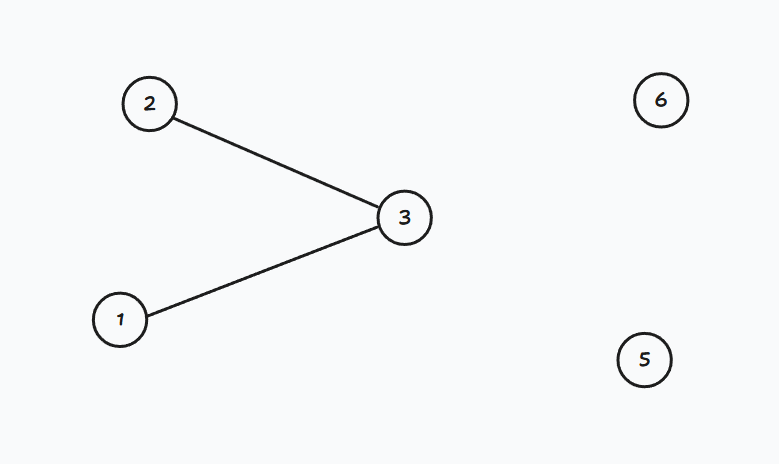
2. 桥
定义:
在一个无向连通图中,如果移除某条边 e 后,图不再连通(分裂成两个连通分量),那么边 e 就被称为桥。
关键性质:
一条边是桥,当且仅当这条边不属于任何一个环。因为如果它在环中,即使移除了它,我们仍然可以通过环上的其他路径在它的两个端点之间通行。
示例:
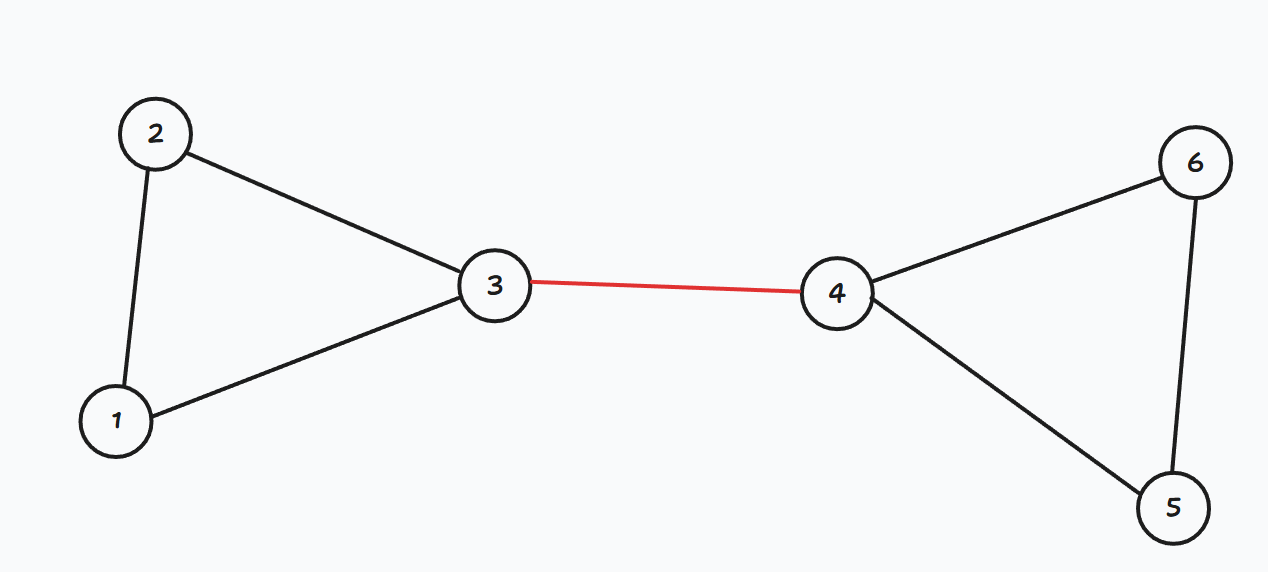
如果将红遍删去,那么图变得不再连通:
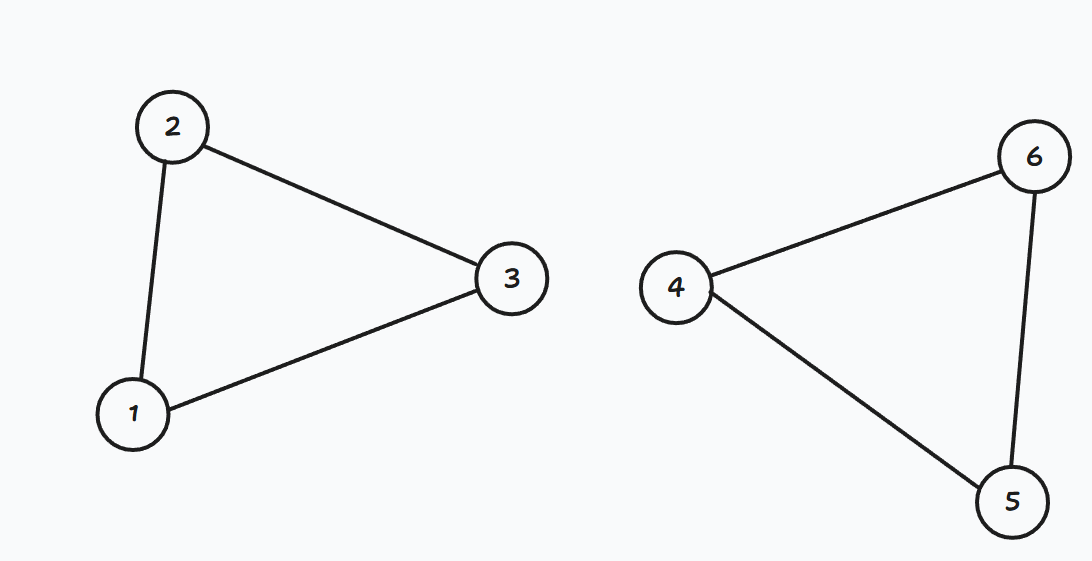
3. 点双连通分量 (v-BCC)
定义:
一个无向图的点双连通分量(简称“点双”)是一个极大的点双连通子图。而一个图被称为点双连通的,需要满足以下两个条件之一:
- 图的顶点数不超过2。
- 图中任意两点之间都至少存在两条点不相交的路径(除了起点和终点,路径上的其他顶点不重复)。
更直观的定义:
一个点双连通分量是一个不包含任何割点的极大子图。换句话说,在点双内部,移除任何一个点,剩下的部分依然是连通的。
通俗理解:
点双是一个“结构稳定”的子网络。在这个子网络内部,任何一个节点(站点)出故障,都不会影响其他节点之间的通信。
关键性质:
- 一个割点可以属于多个点双连通分量。它扮演着连接不同点双的角色。
- 一个非割点只属于唯一一个点双连通分量。
- 图中的任意一条边最多只属于一个点双。
例子:
在下图中:任意删去一条边图任然连通。
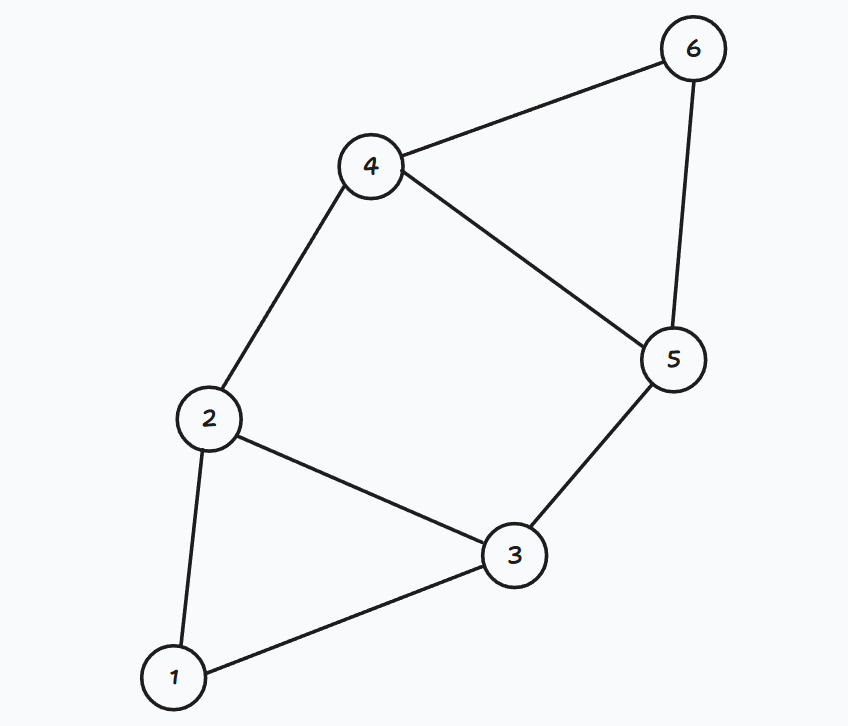
4. 边双连通分量 ( e-BCC)
定义:
一个无向图的边双连通分量(简称“边双”)是一个极大的边双连通子图。而一个图被称为边双连通的,是指图中任意两点之间都至少存在两条边不相交的路径(路径上的边不重复)。
更直观的定义:
一个边双连通分量是一个不包含任何桥的极大子图。换句话说,在边双内部,移除任何一条边,剩下的部分依然是连通的。
通俗理解:
边双也是一个“结构稳定”的子网络,但要求比点双稍弱。在这个子网络内部,任何一条线路(边)中断,都不会影响任意两点之间的连通性。
关键性质:
- 一个图可以被划分成若干个边双连通分量,这些分量之间通过桥连接。
- 每个顶点和每条边都只属于唯一一个边双连通分量。
例子:
在下图中,删去任意的一条边图任然连通。
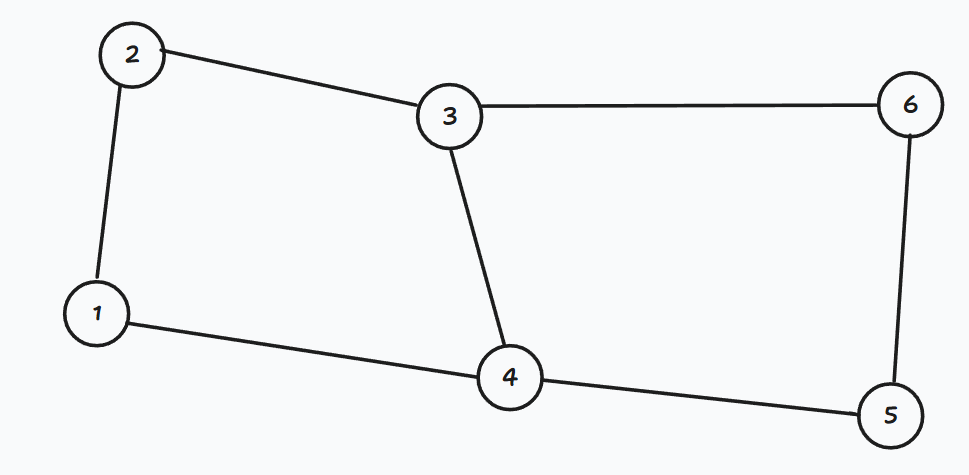
P8436 【模板】边双连通分量
题目描述
对于一个 n n n 个节点 m m m 条无向边的图,请输出其边双连通分量的个数,并且输出每个边双连通分量。
输入格式
第一行,两个整数 n n n 和 m m m。
接下来 m m m 行,每行两个整数 u , v u, v u,v,表示一条无向边。
不保证图为简单图,图中可能有重边和自环。
输出格式
第一行一个整数 x x x 表示边双连通分量的个数。
接下来的 x x x 行,每行第一个数 a a a 表示该分量结点个数,然后 a a a 个数,描述一个边双连通分量。
你可以以任意顺序输出边双连通分量与边双连通分量内的结点。
输入输出样例 #1
输入 #1
5 8
1 3
2 4
4 3
1 2
4 5
5 1
2 4
1 1
输出 #1
1
5 1 5 4 2 3
输入输出样例 #2
输入 #2
5 3
1 2
2 3
1 3
输出 #2
3
3 1 3 2
1 4
1 5
输入输出样例 #3
输入 #3
6 5
1 3
2 4
1 2
4 6
2 3
输出 #3
4
3 1 2 3
1 4
1 5
1 6
输入输出样例 #4
输入 #4
7 8
1 3
2 4
3 5
2 5
6 4
2 5
6 3
2 7
输出 #4
3
1 1
5 2 5 3 6 4
1 7
说明/提示
样例四解释:
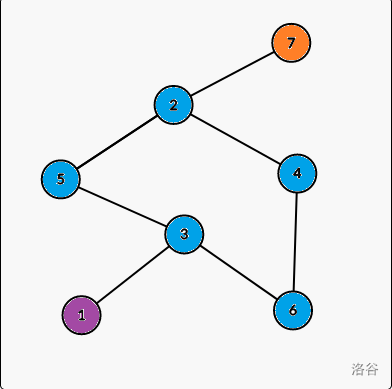
相同颜色的点为同一个连通分量。
数据范围:
对于
100
%
100\%
100% 的数据,
1
≤
n
≤
5
×
1
0
5
1 \le n \le 5 \times10 ^5
1≤n≤5×105,
1
≤
m
≤
2
×
1
0
6
1 \le m \le 2 \times 10^6
1≤m≤2×106。
| subtask | n n n | m m m | 分值 |
|---|---|---|---|
| 1 1 1 | 1 ≤ n ≤ 100 1 \le n \le 100 1≤n≤100 | 1 ≤ m ≤ 500 1 \le m \le 500 1≤m≤500 | 25 25 25 |
| 2 2 2 | 1 ≤ n ≤ 5000 1 \le n \le 5000 1≤n≤5000 | 1 ≤ m ≤ 5 × 1 0 4 1 \le m \le 5 \times 10^4 1≤m≤5×104 | 25 25 25 |
| 3 3 3 | 1 ≤ n ≤ 2 × 1 0 5 1 \le n \le 2\times 10^5 1≤n≤2×105 | 1 ≤ m ≤ 5 × 1 0 5 1 \le m \le 5\times 10^5 1≤m≤5×105 | 25 25 25 |
| 4 4 4 | 1 ≤ n ≤ 5 × 1 0 5 1 \le n \le 5 \times10 ^5 1≤n≤5×105 | 1 ≤ m ≤ 2 × 1 0 6 1 \le m \le 2 \times 10^6 1≤m≤2×106 | 25 25 25 |
正解程序:
#include <bits/stdc++.h>
#define PII pair<int, int>
using namespace std;
// 定义常量,N为点数上限,M为边数上限
const int N = 5e5 + 5;
const int M = 2e6 + 5;
// --- 全局变量 ---
int n, m; // n: 点数, m: 边数
int dfn[N], low[N], tsp; // Tarjan算法核心数组:
// dfn[u]: 节点u的DFS时间戳 (discovery time)
// low[u]: 节点u能追溯到的最早的祖先节点的dfn值
// tsp: 时间戳计数器
int stk[N], top; // 手动实现的栈,用于存储当前DFS路径上的节点
int cnt; // e-BCC (边双连通分量) 的计数器
int id[N];
vector<PII> ed[N]; // 邻接表,存储图结构。
// PII是 {邻接点v, 边(u,v)的编号p}
// --- 存储结果 ---
vector<int> ans[N]; // ans[i] 存储第 i 个 e-BCC 中的所有节点
// Tarjan算法核心函数,用于寻找边双连通分量
// u: 当前访问的节点
void tarjan(int u, int fa)
{
// 1. 初始化当前节点u的dfn和low值
dfn[u] = low[u] = ++ tsp;
// 2. 将当前节点u压入栈中
stk[ ++ top ] = u;
// 3. 遍历u的所有邻接边
for (auto x : ed[u]) {
int v = x.first; // 邻接点
int p = x.second; // 边(u,v)的编号
// Case 1: 邻接点v还未被访问过 (dfn[v] == 0)
// 这意味着 (u,v) 是一条DFS树上的“树边”
if (!dfn[v]) {
tarjan(v, p); // 递归访问v
// 从子节点v回溯后,用v的low值更新u的low值
// 意义是:如果v能回到更早的祖先,那么u也能通过v回到那里
low[u] = min(low[u], low[v]);
// 桥的判断逻辑,这里其实不是必须的,因为SCC的划分逻辑已足够
// 但如果需要单独知道哪些是桥,这行代码是正确的
// if(dfn[u] < low[v]) is[p] = is[p ^ 1] = true;
}
// Case 2: 邻接点v已被访问过,并且(u,v)不是来时的路 (不是父边)
// 这意味着 (u,v) 是一条“返祖边”
else if (p != (fa ^ 1)) {
// 用v的dfn值更新u的low值
// 找到了一个从u回到其祖先v的捷径
low[u] = min(low[u], dfn[v]);
}
}
// 4. 关键:分量划分(SCC的划分逻辑)
// 当一个节点u的dfn值和low值相等时,说明u是其所在e-BCC在DFS树中的根节点
// 同时也意味着,从栈顶到u的所有节点,构成了一个完整的e-BCC
if (dfn[u] == low[u]) {
++cnt; // 发现一个新的e-BCC,分量计数器加一
int tp = -1;
// 反复从栈顶弹出节点,直到u被弹出为止
do {
tp = stk[ top -- ]; // 弹出栈顶节点
ans[cnt].push_back(tp); // 将弹出的节点加入当前分量
// id[tp] = cnt; // 如果需要,也可以标记每个点所属的分量ID
} while (u != tp);
}
}
int main()
{
// 优化输入输出
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m;
// --- 建图 ---
// 使用 k 和 k+1 为一条无向边的两个方向进行唯一编号
// 这样 p 和 p^1 就是互为反向的边,方便判断父边
int k = 0;
for (int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
ed[u].push_back({v, k});
ed[v].push_back({u, k + 1});
k += 2;
}
// --- 运行算法 ---
// 遍历所有节点,确保图不连通(森林)的情况下也能处理所有部分
for (int i = 1; i <= n; i++) {
if (!dfn[i]) { // 如果节点i还未被访问过
tarjan(i, -1); // 从节点i开始进行Tarjan算法,-1表示没有父边
}
}
// --- 输出结果 ---
cout << cnt << endl; // 输出e-BCC的总数
for (int i = 1; i <= cnt; i++) {
cout << ans[i].size(); // 输出当前分量的节点数
for (auto x : ans[i]) {
cout << ' ' << x; // 输出分量内的每个节点
}
cout << endl;
}
return 0;
}
P8435 【模板】点双连通分量
题目描述
对于一个 n n n 个节点 m m m 条无向边的图,请输出其点双连通分量的个数,并且输出每个点双连通分量。
输入格式
第一行,两个整数 n n n 和 m m m。
接下来 m m m 行,每行两个整数 u , v u, v u,v,表示一条无向边。
输出格式
第一行一个整数 x x x 表示点双连通分量的个数。
接下来的 x x x 行,每行第一个数 a a a 表示该分量结点个数,然后 a a a 个数,描述一个点双连通分量。
你可以以任意顺序输出点双连通分量与点双连通分量内的结点。
输入输出样例 #1
输入 #1
5 8
1 3
2 4
4 3
1 2
4 5
5 1
2 4
1 1
输出 #1
1
5 1 2 3 4 5
输入输出样例 #2
输入 #2
5 3
1 2
2 3
1 3
输出 #2
3
1 4
1 5
3 1 2 3
输入输出样例 #3
输入 #3
6 5
1 3
2 4
1 2
4 6
2 3
输出 #3
4
2 6 4
2 4 2
3 3 2 1
1 5
输入输出样例 #4
输入 #4
7 8
1 3
2 4
3 5
2 5
6 4
2 5
6 3
2 7
输出 #4
3
2 7 2
5 5 2 4 6 3
2 3 1
输入输出样例 #5
输入 #5
1 1
1 1
输出 #5
1
1 1
说明/提示
样例四解释:
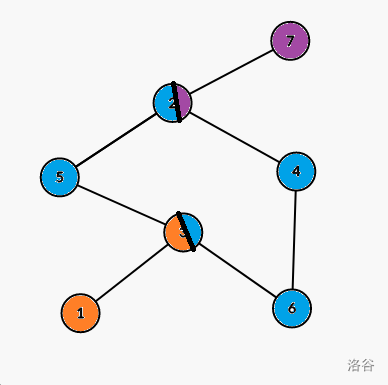
相同颜色的点为同一个分量里的结点。
温馨提示:请认真考虑孤立点与自环(样例五)的情况。
数据范围:
对于
100
%
100\%
100% 的数据,
1
≤
n
≤
5
×
1
0
5
1 \le n \le 5 \times10 ^5
1≤n≤5×105,
1
≤
m
≤
2
×
1
0
6
1 \le m \le 2 \times 10^6
1≤m≤2×106。
| subtask | n n n | m m m | 分值 |
|---|---|---|---|
| 1 1 1 | 1 ≤ n ≤ 100 1 \le n \le 100 1≤n≤100 | 1 ≤ m ≤ 500 1 \le m \le 500 1≤m≤500 | 25 25 25 |
| 2 2 2 | 1 ≤ n ≤ 5000 1 \le n \le 5000 1≤n≤5000 | 1 ≤ m ≤ 5 × 1 0 4 1 \le m \le 5 \times 10^4 1≤m≤5×104 | 25 25 25 |
| 3 3 3 | 1 ≤ n ≤ 2 × 1 0 5 1 \le n \le 2\times 10^5 1≤n≤2×105 | 1 ≤ m ≤ 5 × 1 0 5 1 \le m \le 5\times 10^5 1≤m≤5×105 | 25 25 25 |
| 4 4 4 | 1 ≤ n ≤ 5 × 1 0 5 1 \le n \le 5 \times10 ^5 1≤n≤5×105 | 1 ≤ m ≤ 2 × 1 0 6 1 \le m \le 2 \times 10^6 1≤m≤2×106 | 25 25 25 |
注: 以该题目为例题, 给出点双连通分量的模板, 在模板中,有对与点双的缩点与建图的程序,是题目中没有的。
缩点建图的过程
关键:将每一个割点都建一条包含该割点的V-DCC的无向边。
- 循环遍历所有已找到的 V-DCC,其总数为 c n t cnt cnt
- 定义新顶点:为第 i i i 个 BCC 分配一个新的、唯一的ID----- i d id id
- 遍历当前V-DCC中的每一个原始顶点 u u u
- 检查顶点
u
u
u 是否为割点,如果
u
u
u 是割点,则在新图
h
s
hs
hs 中,在代表 V-DCC 的节点
i
d
id
id 和代表割点的节点
u
u
u 之间添加一条无向边。
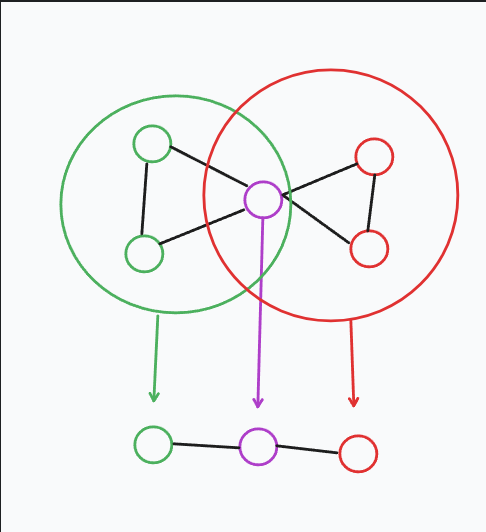
解释:
绿色和红色的两个大圈都是V-DCC, 紫色的是两个V-DCC共用的割点,割点的编号不变,将绿色大圈缩点并赋予一个新的id与割点相连接,红圈同理。😃
模板程序
#include <bits/stdc++.h>
using namespace std;
const int N = 500005; // 原图最大顶点数
const int M = N * 2; // 新图最大节点数 (n个原点 + 最多n个BCC点)
int n, m;
vector<int> ed[N]; // 原图邻接表
// Tarjan 算法所需
int dfn[N], low[N], tsp;
int stk[N], top;
int cnt; // 点双连通分量(BCC)的计数器
bool is[N]; // is[i] = true 表示 i 是割点
// 结果存储
vector<int> dcc[N]; // dcc[i] 存储第 i 个BCC的所有节点
vector<int> hs[M]; // 缩点后新图(块割树)的邻接表
void tarjan(int u, int fa)
{
dfn[u] = low[u] = ++ tsp;
stk[ ++ top ] = u;
int son = 0; // DFS树中子节点计数
for(auto v : ed[u]){
if (v == fa) continue;
if (!dfn[v]) {
son ++ ;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if (low[v] >= dfn[u]) {
// 标记割点
if(fa != 0 || son > 1) is[u] = true;
// 提取BCC
cnt ++ ;
int tp;
do {
tp = stk[top--];
dcc[cnt].push_back(y);
} while (tp != v);
dcc[cnt].push_back(u);
}
}else low[u] = min(low[u], dfn[v]);
}
// 特判:u是一个孤立的连通分量
if(fa == 0 && son == 0){
cnt ++ ;
dcc[cnt].push_back(u);
}
}
void build()
{
for(int i = 1; i <= cnt; ++i){
int bcc_id = n + i; // 为BCC分配新ID
for(auto u : dcc[i]){
if(is[u]){
hs[bcc_id].push_back(u);
hs[u].push_back(bcc_id);
}
}
}
}
int main()
{
ios_base::sync_with_stdio(false);
cin.tie(NULL);
cin >> n >> m;
for (int i = 0; i < m; ++i) {
int u, v;
cin >> u >> v;
if (u == v) continue; // 忽略自环
ed[u].push_back(v);
ed[v].push_back(u);
}
// 2. 运行 Tarjan 算法
for (int i = 1; i <= n; ++i) {
if (!dfn[i]) {
top = 0; // 这可以防止一个连通分量的计算状态污染到下一个。
tarjan(i, 0);
}
}
// 3. 构建新图
build();
// --- 使用和输出部分 ---
// A. 输出BCC (例如P8435模板题的要求)
cout << cnt << "\n";
for (int i = 1; i <= cnt; ++i) {
cout << dcc[i].size() << " ";
for (int node : dcc[i]) {
cout << node << " ";
}
cout << "\n";
}
return 0;
}
感谢观看,如果可以请关注我的洛谷,加入我的洛谷团队(不定期通过)。
Jamig
Jamig的团队
我会不定期在团队中分享高质量题目 😃





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








