文章目录
一、自注意力
在深度学习中,我们经常使用卷积神经网络(CNN)或循环神经网络(RNN)对序列进行编码。现在想象一下,有了注意力机制之后,我们将标记序列输入注意力池化中,以便同一组标记同时充当查询、键和值。具体来说,每个查询都会关注所有的“键-值”对并生成一个注意力输出。由于查询、键和值来自同一组输入,因此执行
自注意力(self-attention):Lin.Feng.Santos.ea.2017,Vaswani.Shazeer.Parmar.ea.2017,也被称为 内部注意力(intra-attention)Cheng.Dong.Lapata.2016,Parikh.Tackstrom.Das.ea.2016,Paulus.Xiong.Socher.2017。在本节中,我们将讨论使用自注意力进行序列编码,包括使用序列的顺序作为补充信息。
1. 自注意力
self-attention的主要作用是找到每个向量和其他向量(包括自己)之间的关联程度。

我们聚焦其中输出 b 1 b^1 b1的计算过程
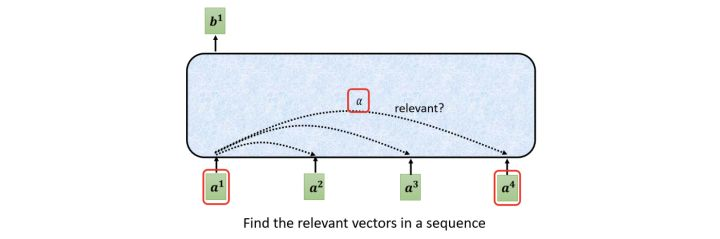
其计算过程为:
- 步骤1:对于每一个输入向量a,分别乘以三个系数 w q 、 w k 、 w v w^q、w^k、w^v wq、wk、wv,得到 q 、 k 、 v q、k、v q、k、v三个值:
q i = w q . a i q^i = w^q.a^i qi=wq.ai写成向量形式: Q = W q . I Q = W^q.I Q=Wq.I
k i = w k . a i k^i = w^k.a^i ki=wk.ai写成向量形式: K = W k . I K = W^k.I K=Wk.I
v i = w v . a i v^i = w^v.a^i vi=wv.ai写成向量形式: V = W v . I V = W^v.I V=Wv.I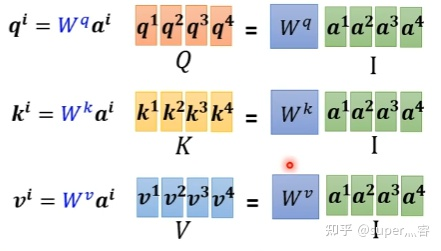
- 步骤2: 利用得到的Q和K计算每两个输入向量之间的相关性,也就是计算attention的值α,α的计算方法有多种,通常采用点乘的方式
α i , j = q i . k j \alpha_{i,j} = q^i . k^j αi,j=qi.kj写成向量形式: A = K T . Q A = K^T.Q A=KT.Q矩阵中每一个值记录了对应的两个输入向量attention的大小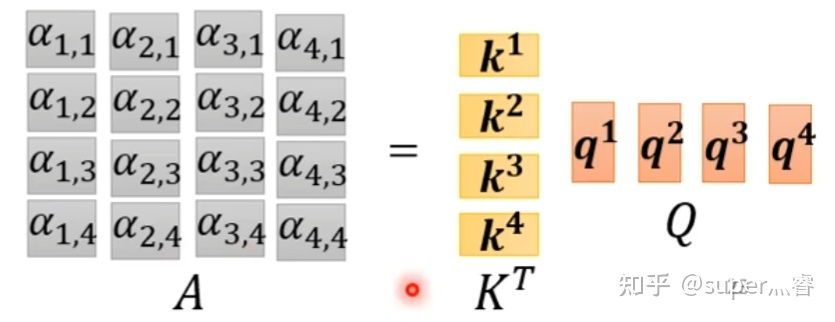
- 步骤3:对A矩阵进行softmax操作或者relu操作得到A’
- 步骤4:利用得到的A’和V计算每个输入向量a对应的self-attention层的输出向量b:
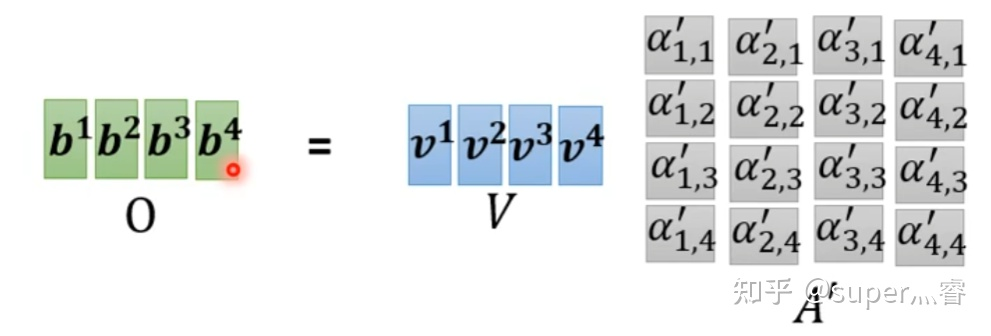
b i = ∑ j = 1 n v i . α i , j ′ b_i = \sum_{j=1}^{n}v^i . \alpha^{'}_{i,j} bi=∑j=1nvi.αi,j′写成向量形式: O = V . A ′ O = V.A^{'} O=V.A′
综上其计算过程为:
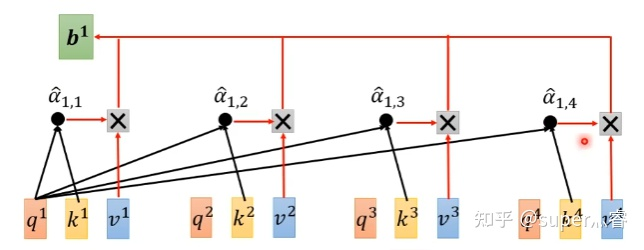
2. 自注意力简单定义和使用
给定一个由标记组成的输入序列 x 1 , … , x n \mathbf{x}_1, \ldots, \mathbf{x}_n x1,…,xn,其中任何 x i ∈ R d \mathbf{x}_i \in \mathbb{R}^d xi∈Rd ( 1 ≤ i ≤ n 1 \leq i \leq n 1≤i≤n),它的自注意力输出为一个长度相同的序列 y 1 , … , y n \mathbf{y}_1, \ldots, \mathbf{y}_n y1,…,yn,其中
y i = f ( x i , ( x 1 , x 1 ) , … , ( x n , x n ) ) ∈ R d \mathbf{y}_i = f(\mathbf{x}_i, (\mathbf{x}_1, \mathbf{x}_1), \ldots, (\mathbf{x}_n, \mathbf{x}_n)) \in \mathbb{R}^d yi=f(xi,(x1,x1),…,(xn,xn))∈Rd
根据注意力池化函数 f f f。下面的代码片段是基于多头注意力对一个张量完成自注意力的计算,张量的形状为(批量大小、时间步的数目或标记序列的长度, d d d)。输出与输入的张量形状相同。
import math
import torch
from torch import nn
from d2l import torch as d2l
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_hiddens, num_hiddens,
num_hiddens, num_heads, 0.5)
attention.eval()
MultiHeadAttention(
(attention): DotProductAttention(
(dropout): Dropout(p=0.5, inplace=False)
)
(W_q): Linear(in_features=100, out_features=100, bias=False)
(W_k): Linear(in_features=100, out_features=100, bias=False)
(W_v): Linear(in_features=100, out_features=100, bias=False)
(W_o): Linear(in_features=100, out_features=100, bias=False)
)
batch_size, num_queries, valid_lens = 2, 4, torch.tensor([3, 2])
X = torch.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens).shape
torch.Size([2, 4, 100])
3. 比较CNN、RNN和Self-Attetion
让我们比较下面几个架构,目标都是将由
n
n
n 个标记组成的序列映射到另一个长度相等的序列,其中的每个输入标记或输出标记都由
d
d
d 维矢量表示。具体来说,我们将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。请注意,顺序操作会妨碍并行计算,而任意的序列位置组合之间的路径越短,则能更轻松地学习序列中的远距离依赖关系 Hochreiter.Bengio.Frasconi.ea.2001 。
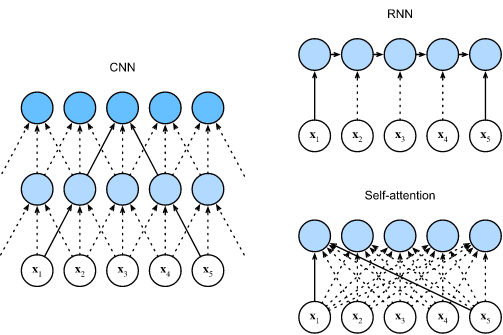
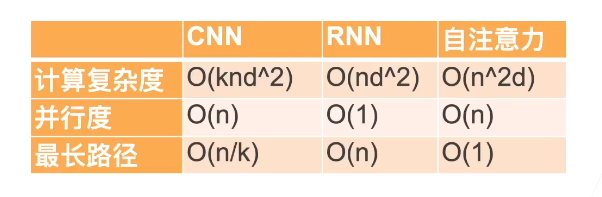
考虑一个卷积核大小为 k k k 的卷积层。我们将在后面的章节中提供关于使用卷积神经网络处理序列的更多详细信息。目前,我们只需要知道,由于序列长度是 n n n,输入和输出的通道数量都是 d d d,所以卷积层的计算复杂度为 O ( k n d 2 ) \mathcal{O}(knd^2) O(knd2)。卷积神经网络是分层的,因此有 O ( 1 ) \mathcal{O}(1) O(1) 个顺序操作,最大路径长度为 O ( n / k ) \mathcal{O}(n/k) O(n/k)。例如, x 1 \mathbf{x}_1 x1 和 x 5 \mathbf{x}_5 x5 处于上图内核大小为 3 的双层卷积神经网络的接受范围内。
当更新循环神经网络的隐藏状态时, d × d d \times d d×d 权重矩阵和 d d d 维隐藏状态的乘法计算复杂度为 O ( d 2 ) \mathcal{O}(d^2) O(d2)。由于序列长度为 n n n,因此循环层的计算复杂度为 O ( n d 2 ) \mathcal{O}(nd^2) O(nd2)。根据对比图,有 O ( n ) \mathcal{O}(n) O(n) 个顺序操作无法并行化,最大路径长度也是 O ( n ) \mathcal{O}(n) O(n)。
在自注意力中,查询、键和值都是 n × d n \times d n×d 矩阵。考虑缩放的”点-积“注意力,其中 n × d n \times d n×d 矩阵乘以 d × n d \times n d×n 矩阵,然后输出的 n × n n \times n n×n 矩阵乘以 n × d n \times d n×d 矩阵。因此,自注意力具有 O ( n 2 d ) \mathcal{O}(n^2d) O(n2d) 计算复杂性。正如我们在对比图中看到的那样,每个标记都通过自注意力直接连接到任何其他标记。因此,有 O ( 1 ) \mathcal{O}(1) O(1) 个顺序操作可以并行计算,最大路径长度也是 O ( 1 ) \mathcal{O}(1) O(1)。
总而言之,卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
3.1 CNN和self-attention
实际上,在处理图像问题时,每一个像素点都可以看成一个三维的向量,维度就是图像的通道数,所以图像也可以看成是很多向量输入到模型,自注意力机制和CNN的概念类似,都是希望网络不仅仅考虑某一个向量,也就是CNN中希望模型不仅仅考虑某一个像素点,而是让模型考虑一个正方形或者矩形的感受野(Receptive field),对于自注意力机制来说,相当于模型自己决定receptive field是怎样的形状和类型。所以其实CNN卷积神经网络是特殊情况下的一种self-attention,self-attention就是复杂版的CNN。参考Blog
相关文章:On the Relationship between Self-Attention and Convolutional Layers
3.2 RNN和self-attention
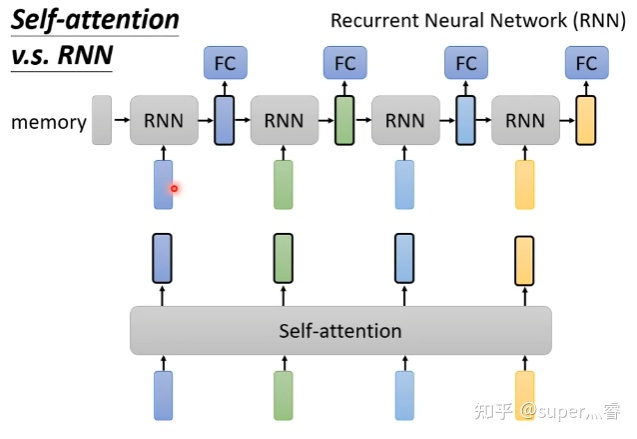
RNN和自注意力机制也类似,都是接受一批输入向量,然后输出一批向量,但RNN只能接受前面的输出作为输入,self-attention可以同时接受所有的向量作为输入,所以一定程度上说Self-attention比RNN更具效率
相关文章:Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
二、位置编码
在处理标记序列时,循环神经网络是逐个的重复地处理标记的,而自注意力则因为并行计算而放弃了顺序操作。为了使用序列的顺序信息,我们通过在输入表示中添加 位置编码(positional encoding)来注入绝对的或相对的位置信息。位置编码可以通过学习得到也可以直接固定得到。接下来,我们描述的是基于正弦函数和余弦函数的固定位置编码Vaswani.Shazeer.Parmar.ea.2017 。
假设输入表示 X ∈ R n × d \mathbf{X} \in \mathbb{R}^{n \times d} X∈Rn×d 包含一个序列中 n n n 个标记的 d d d 维嵌入表示。位置编码使用相同形状的位置嵌入矩阵 P ∈ R n × d \mathbf{P} \in \mathbb{R}^{n \times d} P∈Rn×d 输出 X + P \mathbf{X} + \mathbf{P} X+P,该矩阵在 i t h i^\mathrm{th} ith 行和 ( 2 j ) t h (2j)^\mathrm{th} (2j)th 或 ( 2 j + 1 ) t h (2j + 1)^\mathrm{th} (2j+1)th 列上的元素为
p i , 2 j = sin ( i 1000 0 2 j / d ) , p i , 2 j + 1 = cos ( i 1000 0 2 j / d ) . \begin{aligned} p_{i, 2j} &= \sin\left(\frac{i}{10000^{2j/d}}\right),\\p_{i, 2j+1} &= \cos\left(\frac{i}{10000^{2j/d}}\right).\end{aligned} pi,2jpi,2j+1=sin(100002j/di),=cos(100002j/di).
乍一看,这种基于三角函数的设计看起来很奇怪。在解释这个设计之前,让我们先在下面的 PositionalEncoding 类中实现它。
class PositionalEncoding(nn.Module):
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# Create a long enough `P`
self.P = torch.zeros((1, max_len, num_hiddens))
X = torch.arange(max_len, dtype=torch.float32).reshape(
-1, 1) / torch.pow(
10000,
torch.arange(0, num_hiddens, 2, dtype=torch.float32) /
num_hiddens)
self.P[:, :, 0::2] = torch.sin(X)
self.P[:, :, 1::2] = torch.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
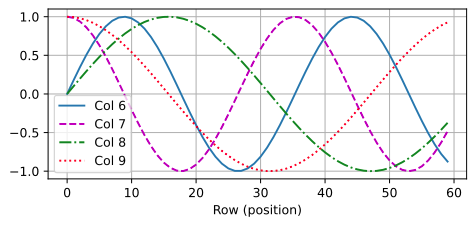
在位置嵌入矩阵 P \mathbf{P} P 中,行表示标记在序列中的位置,列表示位置编码的不同维度。在下面的示例中,我们可以看到位置嵌入矩阵的 6 t h 6^{\mathrm{th}} 6th 和 7 t h 7^{\mathrm{th}} 7th 列的频率高于 8 t h 8^{\mathrm{th}} 8th 和 9 t h 9^{\mathrm{th}} 9th 列。 6 t h 6^{\mathrm{th}} 6th 和 7 t h 7^{\mathrm{th}} 7th 列之间的偏移量( 8 t h 8^{\mathrm{th}} 8th 和 9 t h 9^{\mathrm{th}} 9th 列相同)是由于正弦函数和余弦函数的交替。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.eval()
X = pos_encoding(torch.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(torch.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in torch.arange(6, 10)])
1. 绝对位置信息
为了明白沿着编码维度单调降低的频率与绝对位置信息的关系,让我们打印出 0 , 1 , … , 7 0, 1, \ldots, 7 0,1,…,7 的二进制表示形式。正如我们所看到的,每个数字、每两个数字和每四个数字上的比特值在第一个最低位、第二个最低位和第三个最低位上分别交替。
for i in range(8):
print(f'{i} in binary is {i:>03b}')
0 in binary is 000
1 in binary is 001
2 in binary is 010
3 in binary is 011
4 in binary is 100
5 in binary is 101
6 in binary is 110
7 in binary is 111
在二进制表示中,较高比特位的交替频率低于较低比特位,与下面的热图所示相似,只是位置编码通过使用三角函数在编码维度上降低频率。由于输出是浮点数,因此此类连续表示比二进制表示法更节省空间。
P = P[0, :, :].unsqueeze(0).unsqueeze(0)
d2l.show_heatmaps(P, xlabel='Column (encoding dimension)',
ylabel='Row (position)', figsize=(3.5, 4), cmap='Blues')

2. 相对位置信息
除了捕获绝对位置信息之外,上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移 δ \delta δ,位置 i + δ i + \delta i+δ 处的位置编码可以线性投影位置 i i i 处的位置编码来表示。
这种投影的数学解释是,令 ω j = 1 / 1000 0 2 j / d \omega_j = 1/10000^{2j/d} ωj=1/100002j/d,对于任何确定的位置偏移 δ \delta δ,任何一对 ( p i , 2 j , p i , 2 j + 1 ) (p_{i, 2j}, p_{i, 2j+1}) (pi,2j,pi,2j+1) 都可以线性投影到 ( p i + δ , 2 j , p i + δ , 2 j + 1 ) (p_{i+\delta, 2j}, p_{i+\delta, 2j+1}) (pi+δ,2j,pi+δ,2j+1):
[ cos ( δ ω j ) sin ( δ ω j ) − sin ( δ ω j ) cos ( δ ω j ) ] [ p i , 2 j p i , 2 j + 1 ] = [ cos ( δ ω j ) sin ( i ω j ) + sin ( δ ω j ) cos ( i ω j ) − sin ( δ ω j ) sin ( i ω j ) + cos ( δ ω j ) cos ( i ω j ) ] = [ sin ( ( i + δ ) ω j ) cos ( ( i + δ ) ω j ) ] = [ p i + δ , 2 j p i + δ , 2 j + 1 ] , \begin{aligned} &\begin{bmatrix} \cos(\delta \omega_j) & \sin(\delta \omega_j) \\ -\sin(\delta \omega_j) & \cos(\delta \omega_j) \\ \end{bmatrix} \begin{bmatrix} p_{i, 2j} \\ p_{i, 2j+1} \\ \end{bmatrix}\\ =&\begin{bmatrix} \cos(\delta \omega_j) \sin(i \omega_j) + \sin(\delta \omega_j) \cos(i \omega_j) \\ -\sin(\delta \omega_j) \sin(i \omega_j) + \cos(\delta \omega_j) \cos(i \omega_j) \\ \end{bmatrix}\\ =&\begin{bmatrix} \sin\left((i+\delta) \omega_j\right) \\ \cos\left((i+\delta) \omega_j\right) \\ \end{bmatrix}\\ =& \begin{bmatrix} p_{i+\delta, 2j} \\ p_{i+\delta, 2j+1} \\ \end{bmatrix}, \end{aligned} ===[cos(δωj)−sin(δωj)sin(δωj)cos(δωj)][pi,2jpi,2j+1][cos(δωj)sin(iωj)+sin(δωj)cos(iωj)−sin(δωj)sin(iωj)+cos(δωj)cos(iωj)][sin((i+δ)ωj)cos((i+δ)ωj)][pi+δ,2jpi+δ,2j+1],
2 × 2 2\times 2 2×2 投影矩阵不依赖于任何位置的索引 i i i。
三、小结
- 在自注意力中,查询、键和值都来自同一组输入。
- 卷积神经网络和自注意力都拥有并行计算的优势,而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方,所以在很长的序列中计算会非常慢。
- 为了使用序列的顺序信息,我们可以通过在输入表示中添加位置编码来注入绝对的或相对的位置信息。






















 1163
1163











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










