三色旗问题

三色旗的问题最早由E.W.Dijkstra所提出，他所使用的用语为Dutch Nation Flag（Dijkstra为荷兰人），而多数人会则使用Three-Color Flag来称之。

假设有一条绳子，上面有蓝、白、红三种颜色的旗子，起初绳子上的旗子颜色并没有顺序，您希望将之分类，并排列为蓝、白、红的顺序，要如何移动次数才会最少，注意您只能在绳子上进行这个动作，而且一次只能调换两个旗子。

解法：在一条绳子上移动，意味只能使用一个阵列，而不使用其它的阵列来作辅助，问题的解法很简单（就是3种值的排序），您可以自己想像一下在移动旗子，从绳子开头进行，遇到蓝色往前移，遇到白色留在中间，遇到红色往后移。

如果当前位置W（实际上也会白色有关）所在的位置为白色，则W+1，不处理。如果W部份为蓝色，则B（蓝色指针）与W的元素对调，而B与W必须各+1，表示两个群组都多了一个元素。如果W所在的位置是红色，则将W与R交换，但R（应为R是红色放最后，所以R初始为全部）要减1，表示未处理的部份减1。

注意B、W、R并不是三色旗的个数，它们只是一个移动的指标。一开始时未处理的R指标会是等于旗子的总数，当R的索引数减至少于W的索引数时，表示接下来的旗子就都是红色了，此时就可以结束移动（红色放最后，不管，如果白色和红色指针交叉了，就结束了）。

方法一：调用STL：

输入“red,blue ,white"；就会输出结果

#include <algorithm>  
#include <iostream>    
#include <string>  
#include <vector>  

using namespace std; 

bool compare(const string& x,const string& y)
{
	int a,b;
	if(x=="blue")
		a=1;
	else if(x=="white")
		a=2;
	else a=3;
	if(y=="blue")
		b=1;
	else if(y=="white")
		b=2;
	else b=3;
	return a<b;
}

int main()
{
	vector<string> flags;
	string s;
	cout<<"Place enter your Flags \"End-of-file Ctrl+Z\" : "<<endl;
	while(cin>>s)
	{
		flags.push_back(s);
	}
	sort(flags.begin(),flags.end(),compare);
	cout<<"Result:"<<endl;
	for(vector<string>::size_type i=0;i!=flags.size();++i)
	{
		cout<<flags[i]<<endl;
	}
	system("pause");
	return 0;
}

结果：

缺点：容错性较差，用户输入要求严格；

方法二：

#include<iostream>  
#include<string>  
#include<iomanip>
using namespace std;  

#define N 50  

//BLUE 'b';WHITE 'w';RED 'r' 
int main()  
{ 
	int bflag=0,wflag=0,rflag;  
    char *flags=new char[N];  
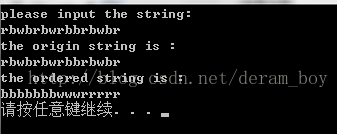
    cout<<"please input the string:"<<endl;  
    cin>>flags;  
    rflag=strlen(flags)-1;  
    cout<<"the origin string is :"<<endl;  
    cout<<flags<<endl;  
    while(wflag<=rflag)  
    {  
        if(flags[wflag]=='w')  
        {  
            wflag++;  
        }  
        else if(flags[wflag]=='b')  
        {  
            swap(flags[wflag],flags[bflag]);  
            wflag++;bflag++;  
        }  
        else  
        {  
            while(wflag<rflag&&flags[rflag]=='r')  
                rflag--;  
            swap(flags[wflag],flags[rflag]);  
            rflag--;  
        }  
    }  
    cout<<"the ordered string is :"<<endl; 
	cout<<flags<<endl;  
	system("pause");
    return 0;  
}