夕拾算法进阶篇：17)01背包和完全背包问题 (动态规划DP)

01背包

问题描述：

有n件物品，每件物品重量为w[i]，价值为c[i]，现有一个容量为V的背包，问如何选取物品放入背包，使得背包内的总价值最大？

问题分析:

令dp[i][v]表示前i件物品(0<=i<=n,0<v<V)恰好装入容量为v的背包中所能获得的最大价值，下面考虑如何求dp[i][v]，考虑第i件物品的选择策略，有如下2中策略：

(1)不放第i件物品，那么问题转换为前i-1件物品放入容量为v的背包中所能获得的最大价值，即dp[i-1][v]。

(2)放第i件物品，那么问题转换为前i-1件物品放入容量为v-w[i]的背包中所能获得的最大价值，即dp[i-1][v-w[i]]+c[i]

由此可以得到其状态转移方程：

                                dp[i][v]=max{dp[i-1][v],dp[i-1][v-w[i]]+c[i]}      (1=<i<=n,w[i]<=v<=V)

其边界为dp[0][v]=0(下面的写法得保证dp始数组初始全为0)，而最后n件物品放入到容量V中的最大价值即dp[n][V]。其代码实现如下：

for(int i=1;i<n;i++){
	for(int v=w[i];v<=V;v++){ //v从w[i]开始是保证下标v-w[i]>=0
		dp[i][v]=max(dp[i-1][v],dp[i-1][v-w[i]]+c[i])
	}
}

其时间和空间算法复杂度皆为O(nV)，但空间复杂度还可以优化，考虑如下图:

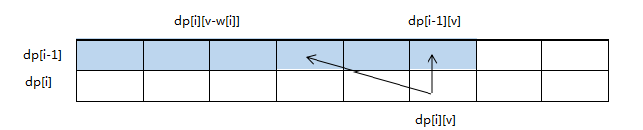
dp[i][v]只和上一行的蓝色位置相关，也就时说求dp[i][v]，只需要上一行的值即可。所以可以使用一维数组保持上一行的dp数组的值。因此其状态转移方程可以改下如下：

                     dp[v]=max(dp[v],dp[v-w[i]]+c[i])    (1<=i<=n,w[i]<=v<=V)

需要注意的是v必须从V开始逆序枚举，因为dp[i][v]右边的已经计算出来的部分是留给下一行使用的，而其左上角的阴影部分是当前需要使用的。若从w[i]开始正向枚举，dp[i][v]左边的值已经是给下一行使用的并覆盖了需要计算的值(ps:完全背包巧好是这情况)，其代码如下：

for(int i=1;i<n;i++){
	for(int v=V;v>=w[i];v--){
		dp[v]=max(dp[v],dp[v-w[i]]+c[i])
	}
}

完全背包

问题描述：

有n种物品，每件物品重量为w[i]，价值为c[i]，现有一个容量为V的背包，问如何选取物品放入背包，使得背包内的总价值最大。其中每种物品都是无穷件。

问题分析：

可以看出，完全背包和01背包的唯一的区别在于：01背包的同种物品只有1件，而完全背包可以无限放入。同样，令dp[i][v]表示前i件物品(0<=i<=n,0<v<V)恰好装入容量为v的背包中所能获得的最大价值，其也有2中选择策略：

(1)不放第i件物品，那么问题转换为前i-1件物品放入容量为v的背包中所能获得的最大价值，即dp[i-1][v]，这和01背包是一样的。

(2)放第i件物品，这里和01背包略有不同。因为完全背包同种物品可以放多件，因此完全背包选择放第i件物品之后并不是转移到了dp[i-1][v-w[i]]，而是转移到了dp[i][v-w[i]]，这是因为放了第i件物品之后，还可以继续放第i件物品，直到第二维的v-w[i]无法保持大于等于0为止。

由此可以得到其状态转移方程

                     dp[i][v]=max{dp[i-1][v],dp[i][v-w[i]]+c[i]}      (1=<i<=n,w[i]<=v<=V)

看上去和01背包神似，唯一的区别就在于max的第二个参数是dp[i]还是dp[i-1]，而这个状态转移方程同样可以改写成一维形式：

                     dp[v]=max(dp[v],dp[v-w[i]]+c[i])    (1<=i<=n,w[i]<=v<=V)

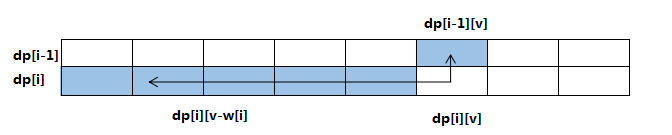
写成一维后和01背包完全相同，唯一的区别在于这里的v是正向枚举的，如下图：

求解dp[i][v]只需要其正上方和左边的值，如果让v从小到大枚举，dp[i][v-[w[i]]的值在上一行就已经计算出来了，而计算出dp[i][v]之后dp[i-1][v]就在也用不到了，可以直接覆盖。其实现的代码如下

for(int i=1;i<n;i++){
	for(int v=w[i];v<=V;v++){
		dp[v]=max(dp[v],dp[v-w[i]]+c[i])
	}
}