入门&普及难度
一、[CSP-J2019] 数字游戏
1. 题目描述
小 K 同学向小 P 同学发送了一个长度为 8 8 8 的 01 字符串来玩数字游戏,小 P 同学想要知道字符串中究竟有多少个 1 1 1。
注意:01 字符串为每一个字符是
0
0
0 或者
1
1
1 的字符串,如 101 为一个长度为
3
3
3 的 01 字符串。
2. 输入格式
输入文件只有一行,一个长度为 8 8 8 的 01 字符串 s s s。
3. 输出格式
输出文件只有一行,包含一个整数,即 01 字符串中字符 1 \mathbf 1 1 的个数。
4. 输入输出样例
输入 #1
00010100
输出 #1
2
输入 #2
11111111
输出 #2
8
5. 说明/提示
样例 1 说明
该 01 字符串中有 2 2 2 个字符 1 1 1。
样例 2 说明
该 01 字符串中有 8 8 8 个字符 1 1 1。
数据规模与约定
- 对于 20 % 20\% 20% 的数据,保证输入的字符全部为 0 0 0。
- 对于 100 % 100\% 100% 的数据,输入只可能包含字符 0 0 0 和字符 1 1 1,字符串长度固定为 8 8 8。
6. 思路
水题一道,遍历判断即可。
7. 参考答案
#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
int main(){
//freopen("game.in","r",stdin);
//freopen("game.out","w",stdout);
string s;
getline(cin,s);
int n=s.length(),cnt=0;
for(int i=0;i<n;i++)
if(s[i]=='1')
cnt++;
cout<<cnt;
//fclose(stdin);
//fclose(stdout);
return 0;
}
二、[CSP-J2019 江西] 面积
1. 题目描述
Alice 有一个边长为 a a a 的正方形,Bob 有一个长宽分别为 b , c b,c b,c 的矩形,请你告诉他们俩谁的图形面积更大。
2. 输入格式
仅一行三个正整数 a , b , c a,b,c a,b,c
3. 输出格式
输出仅一行一个字符串,若正方形面积大则输出 Alice,否则输出 Bob。
4. 输入输出样例
输入 #1
5 4 6
输出 #1
Alice
输入 #2
7 5 10
输出 #2
Bob
5. 说明/提示
数据范围
对于
30
%
30\%
30% 的数据,
1
≤
a
,
b
,
c
≤
100
1 \le a,b,c \le 100
1≤a,b,c≤100,
b
=
c
b=c
b=c;
对于
80
%
80\%
80% 的数据,
1
≤
a
,
b
,
c
≤
1
0
4
1\le a,b,c \le 10^4
1≤a,b,c≤104;
对于
100
%
100\%
100% 的数据,
1
≤
a
,
b
,
c
≤
1
0
9
1\le a,b,c \le 10^9
1≤a,b,c≤109。
样例
1
1
1 解释
正方形面积为
25
25
25,矩形面积为
24
24
24。
样例
2
2
2 解释
正方形面积为
49
49
49,矩形面积为
50
50
50。
6. 思路
水题一道,判断即可。
注意事项:
数据范围中,
1
≤
a
,
b
,
c
≤
1
0
9
1\le a,b,c \le 10^9
1≤a,b,c≤109,说明此题要开 long long。
7. 参考答案
#include<iostream>
#include<cstdio>
using namespace std;
int main(){
//freopen("area.in","r",stdin);
//freopen("area.out","w",stdout);
long long a,b,c;
cin>>a>>b>>c;
if(a*a>b*c)cout<<"Alice";
else cout<<"Bob";
//fclose(stdin);
//fclose(stdout);
return 0;
}
三、[CSP-J 2022] 乘方
1. 题目描述
小文同学刚刚接触了信息学竞赛,有一天她遇到了这样一个题:给定正整数 a a a 和 b b b,求 a b a^b ab 的值是多少。
a b a^b ab 即 b b b 个 a a a 相乘的值,例如 2 3 2^3 23 即为 3 3 3 个 2 2 2 相乘,结果为 2 × 2 × 2 = 8 2 \times 2 \times 2 = 8 2×2×2=8。
“简单!”小文心想,同时很快就写出了一份程序,可是测试时却出现了错误。
小文很快意识到,她的程序里的变量都是 int 类型的。在大多数机器上,int 类型能表示的最大数为
2
31
−
1
2^{31} - 1
231−1,因此只要计算结果超过这个数,她的程序就会出现错误。
由于小文刚刚学会编程,她担心使用 int 计算会出现问题。因此她希望你在
a
b
a^b
ab 的值超过
10
9
{10}^9
109 时,输出一个 -1 进行警示,否则就输出正确的
a
b
a^b
ab 的值。
然而小文还是不知道怎么实现这份程序,因此她想请你帮忙。
2. 输入格式
输入共一行,两个正整数 a , b a, b a,b。
3. 输出格式
输出共一行,如果
a
b
a^b
ab 的值不超过
10
9
{10}^9
109,则输出
a
b
a^b
ab 的值,否则输出 -1。
4. 输入输出样例
输入 #1
10 9
输出 #1
1000000000
输入 #2
23333 66666
输出 #2
-1
5. 说明/提示
对于
10
%
10 \%
10% 的数据,保证
b
=
1
b = 1
b=1。
对于
30
%
30 \%
30% 的数据,保证
b
≤
2
b \le 2
b≤2。
对于
60
%
60 \%
60% 的数据,保证
b
≤
30
b \le 30
b≤30,
a
b
≤
10
18
a^b \le {10}^{18}
ab≤1018。
对于
100
%
100 \%
100% 的数据,保证
1
≤
a
,
b
≤
10
9
1 \le a, b \le {10}^9
1≤a,b≤109。
6. 思路
使用 pow 最原始的写法即可。
注意事项:
十年 OI 一场空,______________。
7. 参考答案
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int a,b;
int main(){
//freopen("power.in","r",stdin);
//freopen("power.out","w",stdout);
cin>>a>>b;
if(a==1)//卡一个hack点
return cout<<1,0;
int ans=1;
for(int i=1;i<=b;i++){
if(ans>1e9/a)
return cout<<-1,0;
ans*=a;
}
cout<<ans;
//fclose(stdin);
//fclose(stdout);
return 0;
}
四、[CSP-J 2024] 扑克牌
1. 题目描述
小 P 从同学小 Q 那儿借来一副 n n n 张牌的扑克牌。
本题中我们不考虑大小王,此时每张牌具有两个属性:花色和点数。花色共有 4 4 4 种:方片、草花、红桃和黑桃。点数共有 13 13 13 种,从小到大分别为 A 23456789 T J Q K \tt{A 2 3 4 5 6 7 8 9 T J Q K} A23456789TJQK。注意:点数 10 10 10 在本题中记为 T \tt T T。
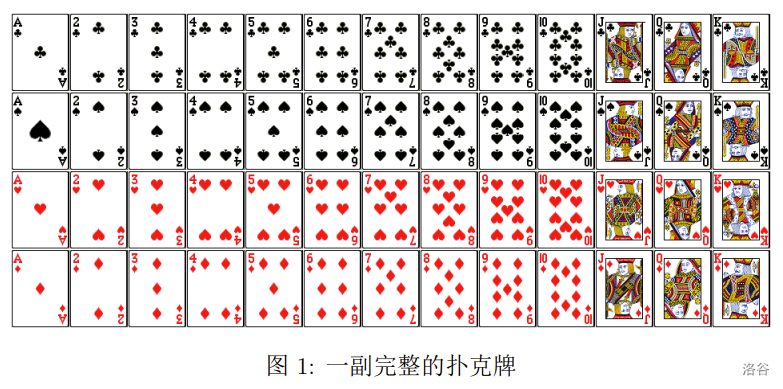
我们称一副扑克牌是完整的,当且仅当对于每一种花色和每一种点数,都恰好有一张牌具有对应的花色和点数。由此,一副完整的扑克牌恰好有 4 × 13 = 52 4 \times 13 = 52 4×13=52 张牌。以下图片展示了一副完整的扑克牌里所有的 52 张牌。
小 P 借来的牌可能不是完整的,为此小 P 准备再向同学小 S 借若干张牌。可以认为小 S 每种牌都有无限张,因此小 P 可以任意选择借来的牌。小 P 想知道他至少得向小 S 借多少张牌,才能让从小 S 和小 Q 借来的牌中,可以选出 52 52 52 张牌构成一副完整的扑克牌。
为了方便你的输入,我们使用字符 D \tt D D 代表方片,字符 C \tt C C 代表草花,字符 H \tt H H 代表红桃,字符 S \tt S S 代表黑桃,这样每张牌可以通过一个长度为 2 2 2 的字符串表示,其中第一个字符表示这张牌的花色,第二个字符表示这张牌的点数,例如 C A \tt{CA} CA 表示草花 A \tt A A, S T \tt{ST} ST 表示黑桃 T \tt T T(黑桃 10)。
2. 输入格式
输入的第一行包含一个整数 n n n 表示牌数。
接下来 n n n 行:
每行包含一个长度为 2 2 2 的字符串描述一张牌,其中第一个字符描述其花色,第二个字符描述其点数。
3. 输出格式
输出一行一个整数,表示最少还需要向小 S 借几张牌才能凑成一副完整的扑克牌。
4. 输入输出样例
输入 #1
1
SA
输出 #1
51
输入 #2
4
DQ
H3
DQ
DT
输出 #2
49
5. 说明/提示
【样例 1 解释】
这一副牌中包含一张黑桃 A \tt A A,小 P 还需要借除了黑桃 A \tt A A 以外的 51 张牌以构成一副完整的扑克牌。
【样例 2 解释】
这一副牌中包含两张方片 Q \tt Q Q、一张方片 T \tt T T(方片 10)以及一张红桃 3,小 P 还需要借除了红桃 3、方片 T \tt T T 和方片 Q \tt Q Q 以外的 49 49 49 张牌。
【样例 3 解释】
见选手目录下的 poker/poker3.in 与 poker/poker3.ans。
这一副扑克牌是完整的,故不需要再借任何牌。
该样例满足所有牌按照点数从小到大依次输入,点数相同时按照方片、草花、红桃、黑桃的顺序依次输入。
【数据范围】
对于所有测试数据,保证: 1 ≤ n ≤ 52 1 \leq n \leq 52 1≤n≤52,输入的 n n n 个字符串每个都代表一张合法的扑克牌,即字符串长度为 2 2 2,且第一个字符为 D C H S \tt{D C H S} DCHS 中的某个字符,第二个字符为 A 23456789 T J Q K \tt{A 2 3 4 5 6 7 8 9 T J Q K} A23456789TJQK 中的某个字符。
::cute-table{tuack}
| 测试点编号 | n ≤ n \leq n≤ | 特殊性质 |
|---|---|---|
| 1 1 1 | 1 1 1 | A |
| 2 ∼ 4 2\sim 4 2∼4 | 52 52 52 | ^ |
| 5 ∼ 7 5\sim 7 5∼7 | ^ | B |
| 8 ∼ 10 8\sim 10 8∼10 | ^ | 无 |
特殊性质 A:保证输入的 n n n 张牌两两不同。
特殊性质 B:保证所有牌按照点数从小到大依次输入,点数相同时按照方片、草花、红桃、黑桃的顺序依次输入。
6. 思路
考虑使用一个数组来存储每一张牌是否出现,最后统计即可。
注意事项:
数字和字符串连续输入时,可以这样:
cin>>n;
cin.ignore();
getline(cin,s);
或者这样:
cin>>n>>s;
7. 参考答案
#include<iostream>
#include<cstdio>
using namespace std;
int n;
bool a[5][15];
int main(){
//freopen("poker.in","r",stdin);
//freopen("poker.out","w",stdout);
//DCHS A23456789TJQK
cin>>n;
string s;
for(int i=1;i<=n;i++){
cin>>s;
int r,c;
if(s[0]=='D')r=1;
if(s[0]=='C')r=2;
if(s[0]=='H')r=3;
if(s[0]=='S')r=4;
if(s[1]=='A')c=1;
if(s[1]=='T')c=10;
if(s[1]=='J')c=11;
if(s[1]=='Q')c=12;
if(s[1]=='K')c=13;
if(isdigit(s[1]))c=s[1]-'0';
a[r][c]=true;
}
int cnt=0;
for(int i=1;i<=4;i++)
for(int j=1;j<=13;j++)
cnt+=!a[i][j];
cout<<cnt;
//fclose(stdin);
//fclose(stdout);
return 0;
}
五、[CSP-J2020] 优秀的拆分
1. 题目描述
一般来说,一个正整数可以拆分成若干个正整数的和。
例如, 1 = 1 1=1 1=1, 10 = 1 + 2 + 3 + 4 10=1+2+3+4 10=1+2+3+4 等。对于正整数 n n n 的一种特定拆分,我们称它为“优秀的”,当且仅当在这种拆分下, n n n 被分解为了若干个不同的 2 2 2 的正整数次幂。注意,一个数 x x x 能被表示成 2 2 2 的正整数次幂,当且仅当 x x x 能通过正整数个 2 2 2 相乘在一起得到。
例如, 10 = 8 + 2 = 2 3 + 2 1 10=8+2=2^3+2^1 10=8+2=23+21 是一个优秀的拆分。但是, 7 = 4 + 2 + 1 = 2 2 + 2 1 + 2 0 7=4+2+1=2^2+2^1+2^0 7=4+2+1=22+21+20 就不是一个优秀的拆分,因为 1 1 1 不是 2 2 2 的正整数次幂。
现在,给定正整数 n n n,你需要判断这个数的所有拆分中,是否存在优秀的拆分。若存在,请你给出具体的拆分方案。
2. 输入格式
输入只有一行,一个整数 n n n,代表需要判断的数。
3. 输出格式
如果这个数的所有拆分中,存在优秀的拆分。那么,你需要从大到小输出这个拆分中的每一个数,相邻两个数之间用一个空格隔开。可以证明,在规定了拆分数字的顺序后,该拆分方案是唯一的。
若不存在优秀的拆分,输出 -1。
4. 输入输出样例
输入 #1
6
输出 #1
4 2
输入 #2
7
输出 #2
-1
5. 说明/提示
样例 1 解释
6 = 4 + 2 = 2 2 + 2 1 6=4+2=2^2+2^1 6=4+2=22+21 是一个优秀的拆分。注意, 6 = 2 + 2 + 2 6=2+2+2 6=2+2+2 不是一个优秀的拆分,因为拆分成的 3 3 3 个数不满足每个数互不相同。
数据规模与约定
- 对于 20 % 20\% 20% 的数据, n ≤ 10 n \le 10 n≤10。
- 对于另外 20 % 20\% 20% 的数据,保证 n n n 为奇数。
- 对于另外 20 % 20\% 20% 的数据,保证 n n n 为 2 2 2 的正整数次幂。
- 对于 80 % 80\% 80% 的数据, n ≤ 1024 n \le 1024 n≤1024。
- 对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 10 7 1 \le n \le {10}^7 1≤n≤107。
6. 思路
经典贪心问题。
7. 参考答案
#include<iostream>
#include<cstdio>
using namespace std;
long long n,a[25];
int main(){
//freopen("split.in","r",stdin);
//freopen("split.out","w",stdout);
cin>>n;
if(n%2==1)
return cout<<-1,0;
a[1]=2;
for(int i=2;i<=25;i++)
a[i]=a[i-1]*2;
while(n)
for(int i=25;i>=1;i--)
if(n>=a[i])
n-=a[i],cout<<a[i]<<" ";
//fclose(stdin);
//fclose(stdout);
return 0;
}




















 2619
2619

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








