后缀数组_后缀数组csdn-CSDN博客

后缀数组——处理字符串的有力工具
后缀数组，很精妙的数据结构。
后缀：从母串的某一位置开始到结尾，suffix(i) = Ai,Ai+1…An。
后缀数组：后缀数组SA是个一维数组，它保存1…n的某个排列SA[1],SA[2]…SA[n]，并且保证suffix(SA[i]) < suffix(SA[i+1])，也就是将S的n个后缀从小到大排好序后的开头位置保存到SA中。
名次数组：名次数组Rank[i]保存的是以i开头的后缀的排名，与SA互为逆。简单的说，后缀数组是“排在第几的是谁”，名次数组是“你排第几”。
为了方便比较，通常在串的末尾添加一个字符，它是从未出现并且最小的字符。

求解后缀数组的算法主要有两种：倍增算法和DC3算法。在这里使用的是许智磊的倍增算法，复杂度为nlogn。
关于详细求解后缀数组的算法，详见许智磊2004国家集训队论文。

后缀数组的应用：
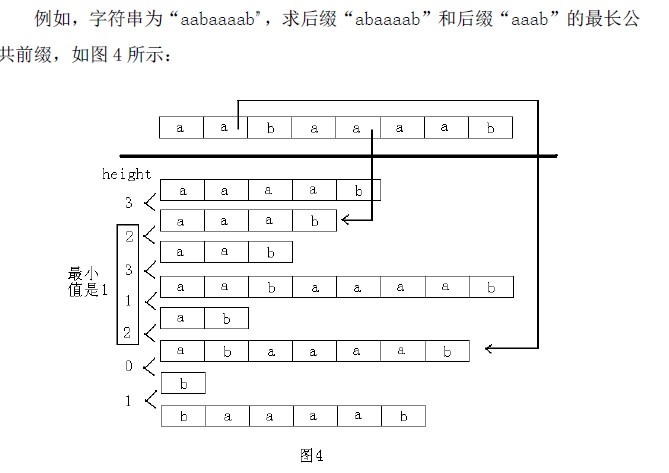
最长公共前缀：先定义height数组，height[i] = suffix(SA[i-1])和suffix(SA[i])的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀。

这里写图片描述

例1：最长公共前缀
给定一个串，求任意两个后缀的最长公共前缀。
解：先根据rank确定这两个后缀的排名i和j(i< j)，在height数组i+1和j之间寻找最小值。(可以用rmq优化)

例2：最长重复子串(不重叠)(poj1743)
解：二分长度，根据长度len分组，若某组里SA的最大值与最小值的差>=len，则说明存在长度为len的不重叠的重复子串。

  int l=1,r=n+1,mid,L,R;  
        bool flag=false;  
        while(l<=r){  
            mid=l+r>>1;  
            L=INF,R=-INF,flag=false;  
            for(int i=1;i<=n;++i){  
                if(height[i]>=mid){  
                    L=min(L,sa[i]);  
                    L=min(L,sa[i-1]);  
                    R=max(R,sa[i]);  
                    R=max(R,sa[i-1]);  
                }else{  
                    if(L+mid+1<=R)flag=true;//这里注意是L+mid+1,因为r[L+mid]=r[L+mid+1]-r[L+mid],从L开始原串中前面那个子串包括L+mid+1   
                    L=INF,R=-INF;  
                }  
            }  
            if(L+mid+1<=R)flag=true;  
            if(flag)l=mid+1;  
            else r=mid-1;  
        }  
        if(l>=5)cout<<l<<endl;  
        else cout<<0<<endl;  
    }

例3：最长重复子串(可重叠)
解：height数组里的最大值。这个问题等价于求两个后缀之间的最长公共前缀。

例4：至少重复k次的最长子串(可重叠)(poj3261)
解：二分长度，根据长度len分组，若某组里的个数>=k，则说明存在长度为len的至少重复k次子串。

例5：最长回文子串(ural1297)
给定一个串，对于它的某个子串，正过来写和反过来写一样，称为回文子串。
解：枚举每一位，计算以这个位为中心的的最长回文子串(注意串长要分奇数和偶数考虑)。将整个字符串反转写在原字符串后面，中间用$分隔。这样把问题转化为求某两个后缀的最长公共前缀。

LL calculate(int n,int len,int k){
    int *mark=wb,*ans=wm,Top=0;//num[1],num[2]分别表示字符串A,B,suffix(0~i-1)和suffix(i)的最长公共子串>=k的总个数
    LL sum=0,num[3]={0};
    for(int i=1;i<=n;++i){
        if(height[i]<k){
            Top=num[1]=num[2]=0;
        }else{
            for(int size=Top;size && ans[size]>height[i]-k+1;--size){//维护单调栈,ans记录的是suffix(j)和suffix(i-1)>=k的最长公共子串的个数,个数越多表示height[j]越大
                num[mark[size]]+=height[i]-k+1-ans[size];//suffix(j)和suffix(i)>=k的最长公共子串只能是长度为k~height[i],所以需要减去(ans[size]-(height[i]-k+1))
                ans[size]=height[i]-k+1;//更新个数(更新单调栈,使栈里面元素非递减)
            }
            ans[++Top]=height[i]-k+1;
            if(sa[i-1]<len)mark[Top]=1;//由于num新增加的结果是suffix(i-1)和suffix(i)的结果,所以是判断sa[i-1] 
            if(sa[i-1]>len)mark[Top]=2;
            num[mark[Top]]+=height[i]-k+1;//增加由suffix(i-1)和suffix(i)产生的结果 
            if(sa[i]<len)sum+=num[2];//表示和suffix(i)产生的结果新增加B串的suffix(0~i-1)和suffix(i)>=k的个数
            if(sa[i]>len)sum+=num[1];//表示和suffix(i)产生的结果新增加A串的suffix(0~i-1)和suffix(i)>=k的个数
        }
    }
    return sum;
}

例6：最长公共子串(poj2774)
给定两个字符串s1和s2，求出s1和s2的最长公共子串。
解：将s2连接到s1后，中间用$分隔开。这样就转化为求两个后缀的最长公共前缀，注意不是height里的最大值，是要满足sa[i-1]和sa[i]不能同时属于s1或者s2。

for(i = 2; i < k; i ++)
        if((sa[i] < l1 && sa[i-1] > l1) || (sa[i-1] < l1 && sa[i] > l1))
        {
            ans = max(ans, height[i]);
        }

例7：长度不小于k的公共子串的个数(poj3415)
给定两个字符串s1和s2，求出s1和s2的长度不小于k的公共子串的个数(可以相同)。
解：将两个字符串连接，中间用$分隔开。扫描一遍，每遇到一个s2的后缀就统计与前面的s1的后缀能产生多少个长度不小于k的公共子串，这里s1的后缀需要用单调栈来维护。然后对s1也这样做一次。

例8：至少出现在k个串中的最长子串(poj3294)
给定n个字符串，求至少出现在n个串中k个的最长子串。
将n个字符串连接起来，中间用$分隔开。二分长度，根据长度len分组，判断每组的后缀是否出现在不小于k个原串中。

const int maxn =20222;

int n,num[maxn];
int sa[maxn],rank[maxn],height[maxn];
int wa[maxn],wb[maxn],wv[maxn],wd[maxn];

int cmp(int *r, int a, int b, int l)
{
    return r[a] == r[b] && r[a+l] == r[b+l];
}

void da(int *r, int n, int m)            //  倍增算法0(nlgn)。
{
    int i, j, p, *x = wa, *y = wb, *t;
    for(i = 0; i < m; i ++) wd[i] = 0;
    for(i = 0; i < n; i ++) wd[x[i]=r[i]] ++;
    for(i = 1; i < m; i ++) wd[i] += wd[i-1];
    for(i = n-1; i >= 0; i --) sa[-- wd[x[i]]] = i;
    for(j = 1, p = 1; p < n; j *= 2, m = p)
    {
        for(p = 0, i = n-j; i < n; i ++) y[p ++] = i;
        for(i = 0; i < n; i ++) if(sa[i] >= j) y[p ++] = sa[i] - j;
        for(i = 0; i < n; i ++) wv[i] = x[y[i]];
        for(i = 0; i < m; i ++) wd[i] = 0;
        for(i = 0; i < n; i ++) wd[wv[i]] ++;
        for(i = 1; i < m; i ++) wd[i] += wd[i-1];
        for(i = n-1; i >= 0; i --) sa[-- wd[wv[i]]] = y[i];
        for(t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i = 1; i < n; i ++)
        {
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j) ? p - 1: p ++;
        }
    }
}

void calHeight(int *r, int n)            //  求height数组。
{
    int i, j, k = 0;
    for(i = 1; i <= n; i ++) rank[sa[i]] = i;
    for(i = 0; i < n; height[rank[i ++]] = k)
    {
        for(k ? k -- : 0, j = sa[rank[i]-1]; r[i+k] == r[j+k]; k ++); 
    }
}

int jude(int k,int m){
    int cnt=1,maxn,minn=sa[1];
    for(int i=2;i<=n;i++){
        if(height[i]>=k){
            cnt++;

        }else{
            cnt=1;

        }
        if(cnt>=m)
        return 1;
    }
    return 0;
}

int main(){

    int k,MAX=0; 
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++){
        scanf("%d",&num[i]);
        MAX=max(MAX,num[i]);
    }
    num[n]=0;
    da(num,n+1,MAX+1);
    calHeight(num,n);
    ....
    ....
    return 0;
}


例子：（注意rank，sa和height3个数组的元素下标）
 n        =  8 ；
 num[]    = { 1, 1, 2, 1, 1, 1, 1, 2, $ }.
 rank[]   = { 4, 6, 8, 1, 2, 3, 5, 7, 0 }.   (rank[0~n-1]为有效值)
 sa[]     = { 8, 3, 4, 5, 0, 6, 1, 7, 2 }.   (sa[1~n]为有效值)
 height[] = { 0, 0, 3, 2, 3, 1, 2, 0, 1 }.   (height[2~n]为有效值)