【Ybtoj 第27章例3】路径长度【期望问题】

最短路径期望算法及其应用

最新推荐文章于 2023-12-21 16:36:49 发布

原创最新推荐文章于 2023-12-21 16:36:49 发布 · 271 阅读

0 ·

CC 4.0 BY-SA版权

Ybtoj 同时被 2 个专栏收录

142 篇文章

订阅专栏

期望

6 篇文章

订阅专栏

该博客介绍了如何使用最短路径期望算法解决图中节点间路径长度的期望值问题。通过Dijkstra的一种变种，文章详细阐述了算法的思路和实现过程，包括邻接表的构建、队列的使用以及权重更新。最后，通过一个实例展示了算法的运行，并给出了C++代码实现，输出了从特定节点到所有其他节点的期望路径长度。

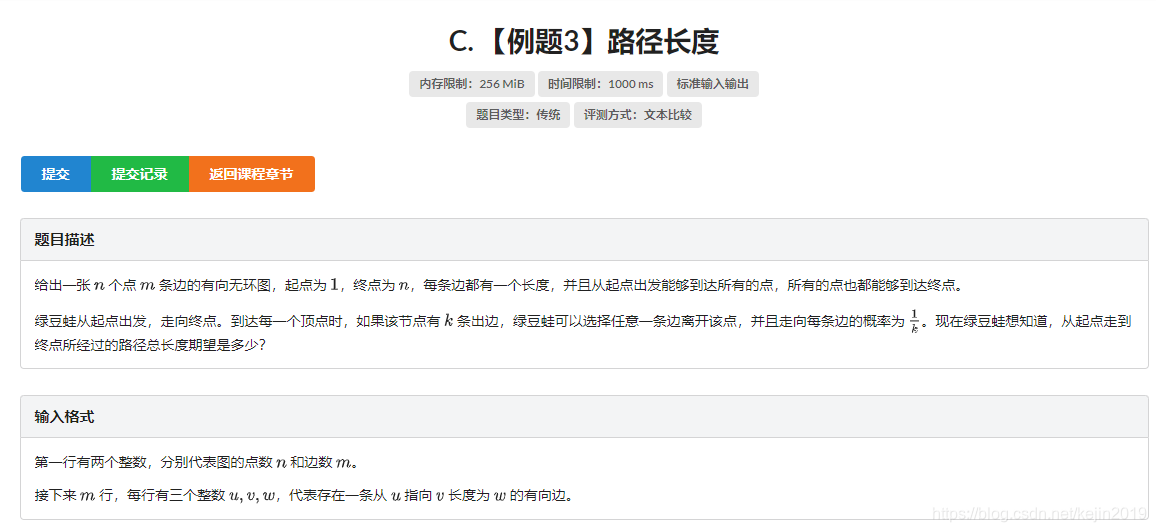
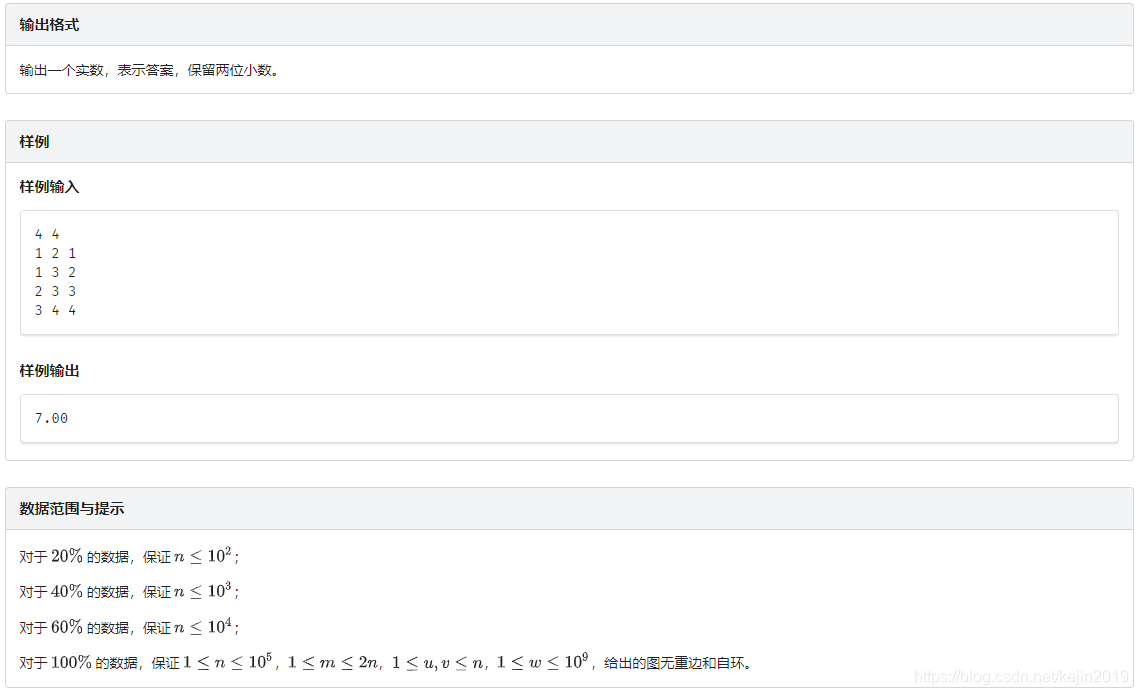
在这里插入图片描述

解题思路

设 $ans_i$ 表示从 $i$ 出发到n nn的路径总长度的期望 $g_i$ 为 $i$ 的出度每个点走向它连的点概率为 $1gi\frac{1}{g_i}$ 就有 $ansi=∑jansj+w(i−>j)gians_i=\sum_j\frac{ans_j+w(i->j)}{g_i}$

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<iomanip>
#include<cstring>
#include<cmath>
#include<map>
#include<queue>
#define ll long long
#define ldb long double
using namespace std;

int n,m,u,v,w,k,num[100010],head[100010],d[100010];
ldb ans[100010];

struct c{
	int x,next,w;
}a[2000010];

void add(int x,int y,int w)
{
	a[++k].x=y;
	a[k].w=w;
	a[k].next=head[x];
	head[x]=k;
}

void work(){
	queue<int> q;
	q.push(n);
	while(!q.empty())
	{
		int x=q.front();q.pop();
		for(int i=head[x];i;i=a[i].next)
		{
			int y=a[i].x;
			d[y]--;
			ans[y]+=(ans[x]+a[i].w)*1.0/num[y]*1.0;
			if(d[y]==0)
				q.push(y);
		}
	}
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d%d",&u,&v,&w);
		add(v,u,w);
		d[u]++;
		num[u]++; 
	}
	work();
	printf("%.2Lf",ans[1]);
}