昨天想的是蚂蚁爬行的绝对距离,晚上睡觉的时候突然想到,可以用蚂蚁爬行相对橡皮筋的比例来计算。
比如说,蚂蚁爬行到了距离终点x的距离,那么只需要再爬行x/l(l为橡皮筋长度)比例的橡皮筋,那么就必定可以到达终点。
按照这个比例的想法,可以比较容易的确定蚂蚁爬行橡皮筋比例的上界与下界。
假设橡皮筋初始长度为l,蚂蚁爬行速度为v1,橡皮筋膨胀速度为v2
将蚂蚁爬行与橡皮筋膨胀两个过程分开
情形1:
假设蚂蚁先爬行,蚂蚁爬行的时候橡皮筋停止膨胀,爬行完毕后橡皮筋再膨胀,膨胀过程中蚂蚁停止
则1轮后,蚂蚁爬行的总距离占整个橡皮筋比例为 v1/l
2轮后,蚂蚁爬行的总距离占整个橡皮筋比例为 v1/(l+v2)
..........
n轮后,蚂蚁爬行的总距离占整个橡皮筋比例为 v1/(l+n*v2)
也就是说n秒后,蚂蚁爬行的距离占整个橡皮筋的比例为:
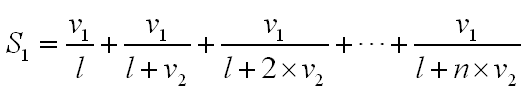
情形2:
假设橡皮筋先膨胀,膨胀过程中蚂蚁停止爬行,膨胀完毕后蚂蚁开始爬行,蚂蚁爬行的时候橡皮筋停止膨胀
则1轮后,蚂蚁爬行的总距离占整个橡皮筋比例为 v1/(l+v2)
2轮后,蚂蚁爬行的总距离占整个橡皮筋比例为 v1/(l+2*v2)
..........
n轮后,蚂蚁爬行的总距离占整个橡皮筋比例为 v1/(l+(n+1)*v2)
也就是说n秒后,蚂蚁爬行的距离占整个橡皮筋的比例为:
显然。蚂蚁在橡皮筋上面爬行的比例应该介于两者之间。
蚂蚁能否爬到终点就是比较s与1的大小。其实只要比较小的那个s2与1的大小就可以了。如果s2能够超过1,那么蚂蚁就能够爬到终点。s2感觉像一个有穷级数,而且,根据前面的模拟实验,这个级数应该是发散的。
问题是,该怎么求这个级数???
有待进一步的探讨。数学太磋了。
续:直接积分,按蚂蚁爬行距离占橡皮筋比例来讨论
假设经过时间t后,蚂蚁到达位置s,此时橡皮筋长度为L=l+v2t。由时间t经过时间dt后,蚂蚁爬行的距离为v1dt,由于时间短很小,因此可假定橡皮筋还来不及拉伸,在这段极短的时间dt内,蚂蚁爬行的距离占整个橡皮长度的比例为:
因此,因此,可以计算得经过时间t后,蚂蚁爬行占橡皮筋比例为:
即:
蚂蚁在经过时间t后的速度为:
观察一下,前面部分是一个常数,后面是一个log函数。验证了昨天的猜测。
经过时间t后蚂蚁距离终点距离为:
(这个距离也可以通过对速度积分来计算)
这个函数就比较复杂了。前面半截为1减去一个log函数,后面半截为一个线性函数,两个相乘,会是什么样子的曲线呢?可以模拟一下。
还有一个很关键的问题,就是,蚂蚁经过多少时间能到达终点?
用 r=1 计算得如下结果:
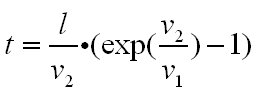
(注意要向上取整)
当l=100,v1=1,v2=10时,答案为:t = 10(e^10-1)=220 255,跟昨天模拟结果的略有差距,误差10s,应该是在时间t较长时,模拟的时间片段显得较大而导致误差。当修改参数使得t减小时,误差应该会变小直至没有误差;若修改参数使得t增大,这个误差会继续扩大。
从上面的公式可以看出,蚂蚁到达终点的时间与 v2/v1 密切相关。
也可以验证 昨天模拟得到的结论: 对蚂蚁速度v1最敏感,橡皮筋速度v2次之,橡皮筋长度l最不敏感
对v1最敏感是因为 v1初始值比较小,稍微修改都可能导致很大的变化。比如v1从1cm/s变到2cm/s,那么时间t就会有10(e^10-1)变到10(e^5-1),两者差e^5倍,这个差距是巨大的;而如果将v2由10cm/s变到20cm/s,差距仅为e^2倍,相比要小很多。







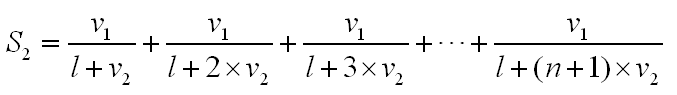
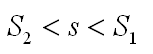
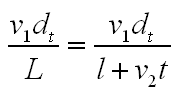
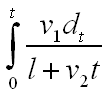
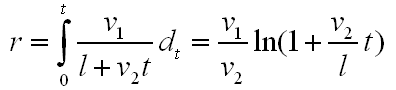
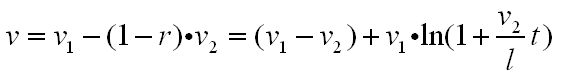
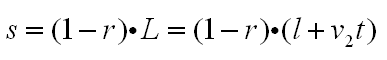














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








