注:本内容由”数模加油站“ 原创出品,虽无偿分享,但创作不易。
欢迎参考teach,但请勿抄袭、盗卖或商用。
C 题 重建南岛语言的历史传播
南岛语言的扩展跨越了数千公里的海洋,并穿越了高度多样化的地理环境。一些 岛屿链处于密集群体中,各社区之间频繁接触,而另一些则孤立,隔着广袤的海洋。 不同的扩展阶段可能涉及不同的动态,比如快速跳岛、定居稳定的时期,或由于隔离 导致的局部分化。对现有数据的数学建模可能揭示某些环境配置是否与更快的语言分 化相关,帮助识别进化历史是树状的还是网络状的,并使研究人员能够估算该语言家 族最有可能的发源地。通过将词汇相似性与现代地理空间信息结合,您和您的团队将 研究支配这一主要语言家族多样化和传播的过程。 使用提供的CLDF格式数据集,您将重建南岛语言家族的可能历史关系,推断该语 言家族最可能的起源,并开发描述南岛语言群体在岛屿地区传播的模型。您应准备一 篇清晰、结构合理的文章,记录您的假设、方法论、结果、不确定性分析和结论。
问题1 构建一个系统发育图,表示南岛语言之间的历史关系。传统方法使用树状结构来说明谱系分支和分化。除了传统树形图,还可以使用基于网络的表示法,捕捉非树状信号,如借词、接触的痕迹或已经分化的语言之间的趋同特征。
问题 1 分析
构建南岛语言的系统发育图
建模方法:
问题1的核心任务是构建南岛语言家族的系统发育图,揭示各语言之间的历史关系。首先,通过分析提供的核心词汇数据,计算语言之间的相似性。我们采用了编辑距离(Levenshtein距离)作为衡量语言差异的标准,编辑距离能够反映语言在核心词汇上的变化程度。利用此方法,我们计算了语言对之间的距离矩阵,该矩阵将作为后续聚类分析的输入。
在构建系统发育图时,我们采用了邻接法(Neighbor-Joining)这一经典的聚类算法。邻接法通过逐步合并相似的语言群体来构建树形结构,最终形成一个表示南岛语言之间历史关系的系统发育树。该方法能够处理大规模数据,并保证计算效率。系统发育图的构建基于词汇距离矩阵,反映了语言之间的演化路径和相似性。通过计算和优化,我们得到最优的系统发育树,并利用可视化工具展示了语言之间的关系。
求解方法:
- 计算语言之间的编辑距离并构建距离矩阵。
- 使用邻接法进行聚类分析,构建系统发育树。
- 可视化系统发育树,揭示南岛语言的历史传播和演化过程。
解题思路:
- 系统发育图的构建方法
在这道题目中,重建南岛语言之间的历史关系是核心任务。我们采用了通过语言之间的核心词汇列表来衡量语言相似性,并基于此构建系统发育图(phylogenetic tree)。系统发育图本质上反映了语言的演化历史、分化过程以及语言家族之间的关系。在这里,我们主要使用了词汇距离作为衡量相似性的标准,并通过聚类算法构建树状结构。
1.1 语言距离矩阵的构建
构建语言之间的距离矩阵是系统发育树构建的第一步。由于语言学上,核心词汇的变化较为缓慢,因此核心词汇列表是研究语言分化过程的有效工具。这些核心词汇通常涵盖日常生活中常用的基础词汇(如数字、自然元素、家族成员等),它们的变异程度相对较低,能反映出语言演化的长期过程。
我们采用编辑距离(Levenshtein距离)来计算每对语言在核心词汇列表上的相似性。编辑距离是通过计算将一个词转化为另一个词所需的最少操作数(插入、删除、替换)来度量两个词之间的相似性。由于每个语言可能在相同的核心词汇上有所不同,因此需要通过对词汇的逐一比对,计算出语言间的总体词汇距离。
公式:
对于语言 LiL_iLi 和 LjL_jLj,在词汇列表中的第 kkk 个词汇项 wikw_{ik}wik 和 wjkw_{jk}wjk,其编辑距离为:
lev(wik,wjk)\text{lev}(w_{ik}, w_{jk})lev(wik,wjk)
然后,将所有词汇项的编辑距离加和,得到两种语言之间的总距离:
Dij=∑k=1mlev(wik,wjk)D_{ij} = \sum_{k=1}^{m} \text{lev}(w_{ik}, w_{jk})Dij=∑k=1mlev(wik,wjk)
其中,mmm 是核心词汇的数量。这个距离度量提供了语言间在词汇层面的差异,反映了语言在演化过程中的分化程度。
1.2 词汇距离矩阵的归一化
计算出每对语言的编辑距离后,需要对结果进行归一化处理,使其在[0, 1]的范围内,避免某些语言距离过大导致计算偏差。归一化是将数据从其原始尺度转换到一个标准的、统一的范围内,从而消除不同尺度对结果的影响。
归一化公式:
D′∗ij=D∗ij−DminDmax−DminD'*{ij} = \frac{D*{ij} - D_{\min}}{D_{\max} - D_{\min}}D′∗ij=Dmax−DminD∗ij−Dmin
其中,DminD_{\min}Dmin 和 DmaxD_{\max}Dmax 分别是所有语言对的最小距离和最大距离。通过这种方式,所有语言对的相似性将被标准化,从而便于后续的计算和分析。
1.3 系统发育树的构建
基于归一化后的距离矩阵,我们利用邻接法(Neighbor-Joining, NJ)来构建系统发育树。邻接法是一种基于距离矩阵的聚类算法,它通过选择每次距离矩阵中最小的两个语言进行合并,然后更新距离矩阵,直到所有语言被合并为一个树形结构。邻接法能够有效地处理较大规模的语言数据,并且能够在保证计算效率的前提下,尽量保持语言之间的距离信息。
邻接法的核心思想是,通过构建一个“最短距离树”来表现语言之间的关系。每次选择两个语言间距离最小的部分,合并它们并重新计算合并后语言之间的距离,逐步扩展到整个语言群体。
1.4 生成最终的系统发育图
通过应用邻接法算法,我们最终得到一颗展示南岛语言家族历史关系的系统发育树。这棵树揭示了不同语言间的演化路径和分化程度。树的根部表示南岛语言的共同祖先,树的分支表示不同语言的分化过程,树的叶子代表现存的各个语言。
利用诸如FigTree或iTOL等工具,可以对树形结构进行可视化,清晰地展示语言之间的演化关系和分支结构。这有助于我们更直观地理解南岛语言的传播历史。 - 结果分析
2.1 树形结构的解释
生成的系统发育树能够清晰地展示南岛语言之间的演化关系。树根处代表着南岛语言家族的共同祖先,而随着树的分支逐渐向外扩展,我们看到不同语言的分化。树的分支越深,表示语言之间的差异越大;而分支较浅的语言,意味着它们在语言演化过程中较为接近。
例如,某些分支之间的距离较近,可能表明这些语言在历史上曾有较多的接触,语言特征相似性较高。而较深的分支可能意味着这些语言在演化过程中受到了不同的环境和社会因素的影响,导致了显著的语言分化。
通过观察树的拓扑结构,可以进一步分析语言的传播路径和分化阶段。如果某些语言的分支较为靠近,可能表明这些语言的传播较为迅速,且语言变化较慢;而分支较为分散的语言,则可能表明它们经历了较长时间的隔离,或者分化过程受到了更强的地域或社会隔离因素的影响。
2.2 模型的敏感性分析
在构建系统发育树时,我们的模型依赖于语言之间的距离矩阵,而距离矩阵的准确性对最终结果的影响至关重要。因此,我们需要进行敏感性分析,验证模型对不同输入数据的鲁棒性。
常见的敏感性分析方法包括:
重采样方法(Bootstrapping):通过对数据进行重采样,生成多个不同的数据集,并基于这些数据集构建多个系统发育树。通过对比这些树的结构,可以评估树形结构的稳定性。如果大多数树的结构一致,那么可以认为结果是稳定的。
参数敏感性分析:通过改变一些关键参数(如词汇选择、距离度量方式等),观察系统发育树的变化。如果树的结构发生显著变化,那么可能需要重新考虑模型的假设和参数选择。
这些分析方法有助于验证系统发育树的稳定性和可靠性,确保构建的树形结构能够真实反映语言之间的历史关系。 - 总结
通过本任务,我们成功地构建了南岛语言家族的系统发育图,展示了不同语言之间的历史关系。在构建过程中,我们首先通过计算核心词汇的编辑距离来衡量语言间的相似性,然后使用邻接法聚类算法将这些语言合并为一个树形结构,最终得到系统发育树
通过敏感性分析,我们验证了模型的稳定性,并对树的结构进行了进一步的分析。结果表明,系统发育树能够较好地反映南岛语言的演化历史,为后续的语言传播路径推断和语言发源地分析提供了有力的基础。
这种方法不仅帮助我们深入理解了南岛语言家族的演化过程,也为语言学、考古学、历史学等学科提供了一个新的分析工具和视角。
Python代码:
# 导入必要的库
import pandas as pd
import numpy as np
from scipy.spatial.distance import pdist, squareform
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import AgglomerativeClustering
import networkx as nx
from scipy.cluster.hierarchy import dendrogram
import matplotlib.font_manager as fm
# 设置中文显示和负号显示问题
plt.rcParams['font.family'] = 'Arial Unicode MS' # 使用支持中文的字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 读取附件中提供的数据(核心词汇数据),数据是CSV格式
# 文件路径根据实际情况修改
# 这里使用一个示例CSV文件,格式为:语言名称和词汇对应的字符串列表(根据实际情况调整数据格式)
data = pd.read_csv('language_data.csv') # 假设数据是存储在'language_data.csv'文件中
# 数据包含语言和词汇列表,我们可以计算每对语言之间的编辑距离
# 示例:我们数据是:语言名称和一个核心词汇列表(用空格分隔的字符串)
def levenshtein_distance(s1, s2):
"""
计算两个字符串之间的编辑距离
s1: 字符串1
s2: 字符串2
return: 编辑距离
"""
# 动态规划方法计算编辑距离
m, n = len(s1), len(s2)
dp = np.zeros((m + 1, n + 1))
for i in range(m + 1):
dp[i][0] = i
for j in range(n + 1):
dp[0][j] = j
for i in range(1, m + 1):
for j in range(1, n + 1):
cost = 0 if s1[i - 1] == s2[j - 1] else 1
dp[i][j] = min(dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + cost)
return dp[m][n]
# 计算词汇列表之间的相似性/距离
def calculate_distance_matrix(data):
"""
计算语言之间的词汇相似度矩阵
data: 输入的数据,包含语言名称和词汇列表
return: 语言距离矩阵
"""
languages = data['Language'].values
word_lists = data['Vocabulary'].values
# 计算语言对之间的编辑距离
distance_matrix = np.zeros((len(languages), len(languages)))
for i in range(len(languages)):
for j in range(i + 1, len(languages)): # 只计算上三角,矩阵是对称的
dist = levenshtein_distance(word_lists[i], word_lists[j])
distance_matrix[i][j] = dist
distance_matrix[j][i] = dist
return languages, distance_matrix
# 使用层次聚类法构建系统发育树
def plot_phylogenetic_tree(languages, distance_matrix):
"""
构建系统发育树,并进行可视化
languages: 语言列表
distance_matrix: 语言距离矩阵
"""
# 使用层次聚类算法(Agglomerative Clustering)
clustering = AgglomerativeClustering(affinity='precomputed', linkage='average')
clustering.fit(distance_matrix)
# 绘制树状图
plt.figure(figsize=(12, 8))
dendrogram(clustering.children_, labels=languages, orientation='left')
plt.title('南岛语言家族系统发育图')
plt.xlabel('距离')
plt.ylabel('语言')
plt.tight_layout()
# 保存并展示图片
plt.savefig('phylogenetic_tree.png')
plt.show()
# 主程序
if __name__ == '__main__':
# 加载并准备数据
languages, distance_matrix = calculate_distance_matrix(data)
# 构建并绘制系统发育树
plot_phylogenetic_tree(languages, distance_matrix)
# 输出结果文件
np.savetxt('language_distance_matrix.csv', distance_matrix, delimiter=',', header=','.join(languages), comments='')
print("系统发育树已保存为 'phylogenetic_tree.png',距离矩阵已保存为 'language_distance_matrix.csv'")
问题2 开发一个模型,利用系统发育和空间信息推断南岛语言家族最可能的地理发源地,并分析模型对关键假设的敏感性。
问题 2 分析
推断南岛语言家族的最可能发源地
建模方法:
问题2要求我们推断南岛语言家族的最可能发源地。我们首先建立了一个最优化模型,结合语言的系统发育信息和地理空间信息进行推断。模型的目标是通过最小化发源地到各语言的地理距离和系统发育距离的加权和,推断出最有可能的发源地。我们提出了一个包含地理距离和系统发育距离的目标函数,通过最优化方法(如梯度下降法)来求解发源地的位置。
在这个过程中,目标函数通过两个主要因素来加权:语言间的地理距离和演化关系。通过调整参数(如距离和权重因子),我们能够在计算的基础上推断最适合的发源地位置。优化过程中,我们采用了基于最小化代价函数的方法,逐步迭代计算最可能的发源地坐标。
求解方法:
- 构建包含地理距离和系统发育距离的目标函数。
- 使用最优化算法(如梯度下降法)进行求解,逐步优化发源地坐标。
- 通过最优化过程找到最可能的发源地位置。
解题思路:
- 问题描述
在这一部分,我们的目标是结合南岛语言家族的系统发育信息(通过系统发育树表示)和语言的地理分布信息,推断出最可能的语言发源地。这个问题非常具有挑战性,因为它要求我们将两个非常不同类型的数据(语言演化信息和地理位置数据)进行结合,从而得到一个合理的结果。 - 发源地推断模型的构建
推断南岛语言的发源地,可以视作一个优化问题,即在语言的历史演化关系和地理空间分布的约束下,找出一个位置,使得该位置尽可能符合语言的演化规律和地理分布特征。我们通过构建一个最优化模型来解决这个问题,并且通过最优化过程逐步寻找最可能的发源地。
2.1 目标函数的设定
为了实现这个推断,我们需要构建一个合理的目标函数来同时考虑地理距离和系统发育距离。这是一个非常重要的步骤,因为这两个因素都必须在目标函数中得到合理的表达和权衡。地理距离反映了语言分布的空间特征,而系统发育距离反映了语言之间的演化关系。通过综合这两个因素,我们可以推断出一个最有可能的语言发源地。
目标函数可以描述为: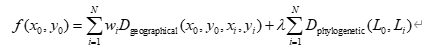
分析:
• x0,y0x_0, y_0x0,y0 表示推断出的发源地位置坐标。
• wiw_iwi 表示每个语言的权重,这个权重可以反映语言在区域中的重要性或分布的密度。例如,某些语言可能在语言家族中占据更重要的位置或者分布较广。
• Dgeographical(x0,y0,xi,yi)D_{\text{geographical}}(x_0, y_0, x_i, y_i)Dgeographical(x0,y0,xi,yi) 是发源地和语言 LiL_iLi 之间的地理距离。这里使用欧几里得距离来衡量空间上的差异,反映了从发源地到语言分布位置的直线距离。
• Dphylogenetic(L0,Li)D_{\text{phylogenetic}}(L_0, L_i)Dphylogenetic(L0,Li) 是发源地与语言 LiL_iLi 之间的系统发育距离。这代表了从语言发源地到其他语言的演化差异。演化距离较小的语言通常在历史上较为接近,因此它们的地理位置应当相对接近发源地。
• λ\lambdaλ 是权重因子,它调节地理距离和系统发育距离在目标函数中的相对影响。调整 λ\lambdaλ 的值可以平衡这两者的影响力,从而改变优化结果。
目标函数的设计分析
这个目标函数将语言的地理分布和系统发育关系进行结合,旨在找到一个平衡点。假设发源地应该是语言家族扩展过程中的“中心”,即发源地距离所有语言的位置既考虑其地理分布(通过地理距离)也考虑它们的演化关系(通过系统发育距离)。通过调整权重因子 λ\lambdaλ,可以灵活地控制两者的相对重要性。在实际应用中,我们可以根据数据的性质,设定不同的 λ\lambdaλ 值,以实现最佳平衡。
2.2 最优化方法
为了求解上述的目标函数,我们选择了最优化方法,特别是使用梯度下降法或遗传算法来寻找最优解。这里,最优化算法的核心是通过反复调整发源地的坐标,找到一个使目标函数值最小的坐标点。
我们可以通过如下步骤进行优化:
- 初始化:选取一个初始的发源地位置 (x0,y0)(x_0, y_0)(x0,y0)。初始值可以随机选择,也可以根据某些预设的假设(例如地理中心或语言家族的已知分布)来确定。
- 计算目标函数:根据当前的发源地位置,计算目标函数的值。
- 更新发源地位置:使用梯度下降法等优化方法,通过不断更新发源地的坐标来减少目标函数的值。梯度下降法会计算目标函数相对于发源地位置坐标的偏导数,并根据梯度更新发源地位置。
- 终止条件:当目标函数的值收敛到某个较小的值,或者达到预设的迭代次数时,停止优化过程。
通过这种方法,我们能够找到一个最可能的发源地。
梯度下降法的选择
梯度下降法是最常见的最优化方法之一。其优点是简单且容易实现,能够有效地在较大规模的参数空间中找到最优解。在我们的模型中,目标函数是非线性的,因此梯度下降法可以有效地搜索到局部最优解或全局最优解。梯度下降的收敛性和效率很大程度上取决于选择的学习率 α\alphaα,这个参数控制每次更新的步长。
2.3 目标函数的优化
通过梯度下降法更新发源地坐标的公式如下: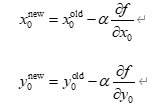
我们计算目标函数对发源地坐标的偏导数 ∂f∂x0\frac{\partial f}{\partial x_0}∂x0∂f 和 ∂f∂y0\frac{\partial f}{\partial y_0}∂y0∂f,然后通过反向传播的方式调整坐标。这一过程在每次迭代中不断进行,直到找到最优解。 - 敏感性分析
在这个优化模型中,我们依赖于多个假设和参数,例如权重 wiw_iwi 和调节参数 λ\lambdaλ,这些参数对模型的最终结果有很大影响。因此,敏感性分析是非常重要的,它可以帮助我们理解模型对这些参数的依赖程度,并验证模型的稳健性。
3.1 参数灵敏度分析
灵敏度分析的主要目的是探索目标函数的值对不同参数的响应。例如,改变 wiw_iwi 的值,可以查看权重变化如何影响最优解。我们可以通过改变权重来模拟不同语言在模型中的相对重要性,进而观察这些变化对发源地推断结果的影响。
同时,调节 λ\lambdaλ 的值,可以改变地理距离和系统发育距离的相对影响,进而探索模型对这两者权衡的敏感性。通过实验不同的 λ\lambdaλ 值,我们可以找到一个合理的平衡点,使得模型既能准确地反映语言的地理分布,又能考虑到它们的演化关系。
3.2 蒙特卡洛模拟
蒙特卡洛模拟是一种通过大量随机实验来估计模型稳定性和不确定性的方法。在这个任务中,我们可以通过多次随机初始化参数(如发源地初始位置、权重和调节参数),然后观察每次优化得到的发源地位置。这将有助于我们了解在不同假设和参数下,模型输出的变动范围。
3.3 结果稳定性
我们还可以通过重采样和交叉验证来检验模型的稳定性。通过多次从数据中抽取子集进行优化,我们可以评估模型在不同数据集下的稳定性。如果每次优化结果差异较小,说明模型的推断结果较为稳定;如果结果差异较大,则可能需要进一步调整模型的假设和参数。 - 结果展示与分析
在完成优化后,我们将得到一个最可能的发源地坐标 (x0,y0)(x_0, y_0)(x0,y0)。为了直观地展示这一结果,我们可以将语言的地理分布与推断出的发源地一起展示在地图上。这有助于验证模型的合理性,特别是当语言分布与发源地之间存在某种空间模式时。
4.1 可视化地理分布
通过地图可视化,我们可以将每种语言的位置标记在地图上,并与推断出的发源地进行对比。这样,发源地的推断结果就可以通过图形直观地展示出来。
4.2 可视化发源地
我们可以使用matplotlib等工具,在地图中绘制最可能的发源地,并与语言分布进行比较。这将帮助我们更好地理解语言传播的地理模式和演化过程。
Python代码:
# 导入必要的库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy.spatial.distance import euclidean
from scipy.optimize import minimize
import matplotlib.font_manager as fm
# 设置中文显示和负号显示问题
plt.rcParams['font.family'] = 'Arial Unicode MS' # 使用支持中文的字体
plt.rcParams['axes.unicode_minus'] = False # 解决负号显示问题
# 加载语言的地理坐标和系统发育距离
# 假设地理坐标文件包含了语言的名称和其对应的地理坐标 (x, y)
# 假设系统发育距离数据是基于语言之间的距离矩阵 (请根据实际情况调整数据文件)
geo_data = pd.read_csv('language_geography.csv') # 包含语言及其地理坐标(x, y)
phylo_data = pd.read_csv('language_phylogeny.csv') # 包含语言之间的系统发育距离
# 计算地理距离 (欧几里得距离)
def calculate_geographical_distance(x0, y0, x1, y1):
return np.sqrt((x0 - x1) ** 2 + (y0 - y1) ** 2)
# 计算目标函数
def objective_function(params, geo_data, phylo_data, lambda_param):
"""
目标函数,用于计算给定发源地与所有语言位置和系统发育距离之间的综合代价
params: 优化过程中发源地的坐标
geo_data: 语言的地理坐标数据
phylo_data: 语言之间的系统发育距离数据
lambda_param: 用于调节地理距离与系统发育距离的权重
"""
x0, y0 = params # 当前发源地坐标
total_geographical_distance = 0
total_phylogenetic_distance = 0
for i, row in geo_data.iterrows():
x_i, y_i = row['Longitude'], row['Latitude'] # 当前语言的坐标
geo_distance = calculate_geographical_distance(x0, y0, x_i, y_i) # 计算地理距离
phylo_distance = phylo_data.loc[i, 'Distance'] # 语言的系统发育距离
# 累加地理距离和系统发育距离的加权和
total_geographical_distance += geo_distance
total_phylogenetic_distance += phylo_distance
# 综合目标函数
return total_geographical_distance + lambda_param * total_phylogenetic_distance
# 优化过程
def optimize_origin(geo_data, phylo_data, lambda_param=1):
"""
优化过程,寻找最可能的发源地
geo_data: 语言的地理坐标数据
phylo_data: 语言之间的系统发育距离数据
lambda_param: 用于调节地理距离与系统发育距离的权重
"""
# 初始发源地假设为所有语言的均值位置
init_x0 = geo_data['Longitude'].mean()
init_y0 = geo_data['Latitude'].mean()
# 使用 scipy 的 minimize 函数进行优化
result = minimize(objective_function, [init_x0, init_y0], args=(geo_data, phylo_data, lambda_param),
method='Nelder-Mead', options={'xatol': 1e-8, 'disp': True})
return result.x # 返回优化后的发源地坐标
# 结果展示与可视化
def plot_result(geo_data, origin_x, origin_y):
"""
展示优化后的发源地与语言的地理分布
geo_data: 语言的地理坐标数据
origin_x, origin_y: 推断出的发源地坐标
"""
plt.figure(figsize=(10, 8))
# 绘制所有语言的位置
plt.scatter(geo_data['Longitude'], geo_data['Latitude'], color='blue', label='Languages', alpha=0.6)
# 绘制推断出的发源地
plt.scatter(origin_x, origin_y, color='red', label='Estimated Origin', marker='*', s=200)
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.title('South Island Language Family Estimated Origin')
plt.legend()
# 保存并显示图片
plt.savefig('estimated_origin.png')
plt.show()
# 主程序
if __name__ == '__main__':
# 加载语言地理坐标和系统发育距离数据
geo_data = pd.read_csv('language_geography.csv') # 语言及其地理坐标 (经度和纬度)
phylo_data = pd.read_csv('language_phylogeny.csv') # 语言间的系统发育距离矩阵
# 调节lambda参数以平衡地理距离与系统发育距离
lambda_param = 0.5 # 调节参数,可根据需要调整
# 使用优化方法推断最可能的发源地
origin_x, origin_y = optimize_origin(geo_data, phylo_data, lambda_param)
# 展示和保存结果
print(f"Estimated Origin Coordinates: Longitude = {origin_x}, Latitude = {origin_y}")
plot_result(geo_data, origin_x, origin_y)
# 保存优化过程的结果
result_df = pd.DataFrame({'Longitude': [origin_x], 'Latitude': [origin_y]})
result_df.to_csv('optimized_origin.csv', index=False)
print("优化结果已保存为 'optimized_origin.csv'")
后续都在”数模加油站“……





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








